2.感知机

时间：2020-01-26 11:40:01 阅读：130 评论：0 收藏：0 [点我收藏+]

1. 感知机模型

输入为实例的特征向量，输出为实例的类别，取+1和-1；感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型；导入基于误分类的损失函数；利用梯度下降法对损失函数进行极小化；感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式；1957年由Rosenblatt提出，是神经网络与支持向量机的基础。定义：假设输入空间（特征空间）是x⊆Rn，输出空间是 Y＝{+1,-1}。输入x?x表示实例的特征向量，对应于输入空间（特征空间）的点；输出y? Y表示实例的类别。由输入空间到输出空间的如下函数：

称为感知机。其中， w和b为感知机模型参数， w?Rn叫作权值（weight）或权值向量（weight vector）， b?R叫作偏置（bias）， w·x表示w和x的内积。 sign是符号函数，即。

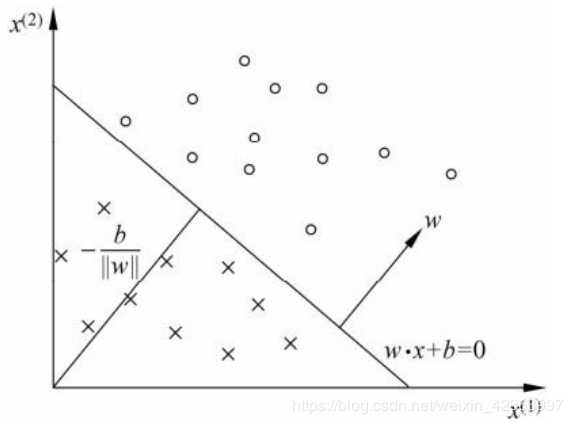
感知机几何解释：
线性方程：

对应于超平面S， w为法向量， b截距，分离正、负类：
分离超平面：

技术图片

2. 感知机学习策略
如何定义损失函数？
自然选择：误分类点的数目，但损失函数不是w,b 连续可导，不宜优化。
另一选择：误分类点到超平面的总距离。
距离：

误分类点：

误分类点距离：：

假设超平面S的误分类点集合为M，那么所有误分类点到超平面S的总距离为：

不考虑，就得到感知机学习的损失函数。给定训练数据集

其中， xi?x＝Rn， yi? Y＝{+1,-1}， i＝1,2,…,N。感知机sign(w·x+b)学习的损失函数定义为

其中M为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。

3. 感知机学习算法

求解最优化问题：

随机梯度下降法，
首先任意选择一个超平面， w， b，然后不断极小化目标函数,损失函数L的梯度：

技术图片

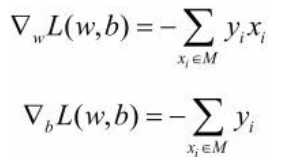
选取误分：

技术图片

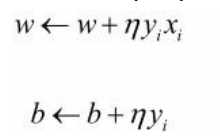
感知机学习算法的原始形式
输入：训练数据集T＝{(x1， y1),(x2,y2),…,(xN,yN)}，其中xi?x＝Rn， yi? ＝{-1,+1}， i＝1,2,…,N；学习率 (0< ≤1)；
输出： w,b；感知机模型f(x)＝sign(w·x+b)。
（1）选取初值w0,b0
（2）在训练集中选取数据(xi， yi)
（3）如果yi(w·xi+b)≤0：

（4）转至（2），直至训练集中没有误分类点。

这个可以说是最简单的感知机算法了，下面是用随机梯度下降实现的代码：

# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:
def __init__(self):
self.w = np.ones(len(data[0])-1, dtype=np.float32)
self.b = 0
self.l_rate = 0.1
# self.data = data

def sign(self, x, w, b):
y = np.dot(x, w) + b
return y

# 随机梯度下降法
def fit(self, X_train, y_train):
is_wrong = False
while not is_wrong:
wrong_count = 0
for d in range(len(X_train)):
X = X_train[d]
y = y_train[d]
if y * self.sign(X, self.w, self.b) <= 0:
self.w = self.w + self.l_rate*np.dot(y, X)
self.b = self.b + self.l_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return ‘Perceptron Model!‘