标签:span 选择 参数取值 无法 一个 inf 相同 高级 UNC
所谓正则化是在代价函数的基础上进行的
为了使costfunction尽快的取得最小值
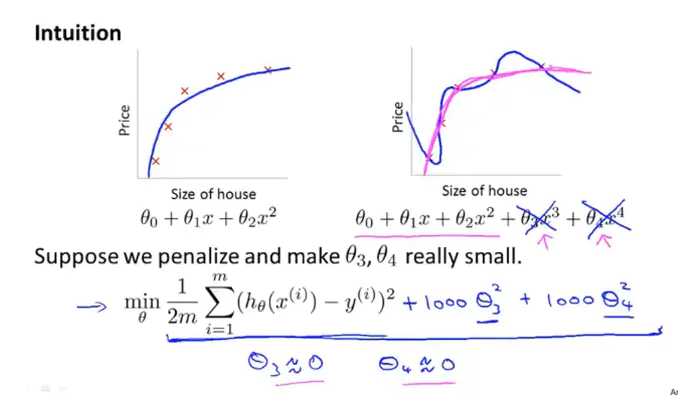
当参数过多时,会存在过拟合现象,假如我们在损失函数中加入一项作为惩罚,如加入\(1000 \theta_{3}^{2}\),当参数\(\theta_{3}\)过大时,会使得损失函数变大,而我们的目标是损失函数最小化,因此,会迫使参数值变小,当但数值值趋近于0时,近似于新加入的项入\(1000 \theta_{3}^{2}\)趋近于0,相当于去掉这一项,此时,模型又近似于二次函数形式。解决了过拟合问题。
感觉确实很不错的

当参数很多时,无法确定那些参数对模型影响大,哪些影响较小。无法对参数进行选择约束。因此,我们就从整体上对参数进行约束,加入上图紫色的正则项,对除\theta _{0} 以外的所有参数进行约束。\lambda 为正则参数。
加入正则项之后的损失函数
\(J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]\)
当正则参数取值较大时,惩罚作用较大,会使得所有参数的取值近似于0,此时,会使得假设模型中参数项以外的项趋近于0,假设模型近似于一条直线,造成欠拟合。
\(J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]\)
加入正则项以后,目标依旧是找到最小化损失函数对应的参数值。通常有两种方法,梯度下降与正规方程

在正则化损失函数中,梯度下降的原理与线性回归中一样,只是在迭代过程中将\(\theta_{0}\)单独分列出来,因为在正则化过程中只对\(\theta_{1}-\theta_{n}\)进行惩罚。在对\(\theta_{1}-\theta_{n}\)进行梯度下降时,加入正则项。化简后的梯度下降迭代公式如上图最后一个公式所示,第一项中的(\(1-\alpha \frac{\lambda}{m}\))是一个略小于1的数,假设为0.99,第二项与原梯度下降公式相同,因此,在进行每次迭代时,都是将原参数乘以0.99,每次迭代将参数缩小一点。
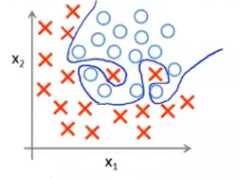
\(\begin{aligned} h_{\theta}(x)=& g\left(\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{1}^{2}\right)_{1}^{2} \\ &+\theta_{3} x_{1}^{2} x_{2}+\theta_{4} x_{1}^{2} x_{2}^{2} \\ &\left.+\theta_{5} x_{1}^{2} x_{2}^{3}+\ldots\right) \end{aligned}\)
损失函数
\(J(\theta)=-\left[\frac{1}{m} \sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]\)

在正则化的logistic回归模型中进行梯度下降的方式与线性回归中的方式相似,上图方括号中的式子为正则化后的损失函数。但是这里对\(h_{\theta } (x)\)的定义与线性回归中的不同,这里表示的是一个sigmoid函数。
高级优化算法
略,等我学通到补充
标签:span 选择 参数取值 无法 一个 inf 相同 高级 UNC
原文地址:https://www.cnblogs.com/gaowenxingxing/p/12234205.html