计算复杂度理论的入门内容

标签：upload   mini   oom   term   center   spl   cdn   splay   内容   

• 决定性问题（Decision problem）：指在某些形式系统回答是或否的问题。例如，“给定两个数字 \(x\) 与 \(y\)，\(x\) 是否可以整除 \(y\) ？”

在计算复杂度的领域中，分类可决定问题的依据在于此问题有多难被解决，难是以解决问题最有效率的算法的计算资源为依据的。

• P 问题（多项式问题，Polynomial problem）：在多项式复杂度内可以被解决的问题。

• NP 问题（非决定性多项式问题，Non-deterministic Polynomial problem）：在多项式复杂度内可以被验证其正确性的问题。

\[ \text{P}\subseteq \text{NP} \]

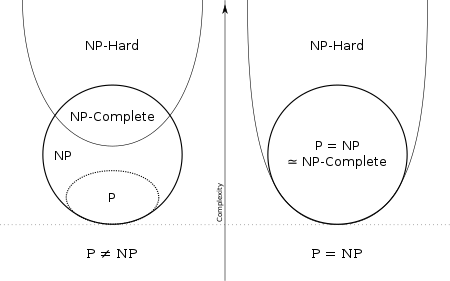
• P/NP 问题：世纪难题 \(\text{P}\overset{?}{=}\text{NP}\)。

• 归约：指讲某个计算问题转换为另一个问题的过程。

• NP 困难（NP-hardness，NP-hardness）：如果所有 NP 问题都可以多项式复杂度归约到某个问题，则称该问题为 NP 困难。

• NP 完全（NP 完备，NPC，NP-Complete）：如果所有 NP 问题都可以多项式复杂度归约到某个 NP 问题，则称该问题为 NP 完全。

\[ \text{NPC}=\text{NP }\cap\text{ NP-hard} \]