标签:spl nim span 回归 一个 isp 学习 play math
为了获得非线性假设空间,我们引入神经网络模型。之前文章提到,对于分类问题,对数几率回归结合多项式特征可以得到非线性决策边界;而将多项式特则与线性回归结合也可以拟合非线性函数。既然我们已经可以得到非线性假设空间,为什么还要引入神经网络模型呢?这是因为当数据集特征数\(d\)增大时,高阶多项式项的数量将以几何级数递增,特征空间也随之急剧膨胀。因此,我们需要神经网络模型来解决复杂的非线性问题。
如图所示,神经网络模型通常按照一个输入层、若干隐藏层以及一个输出层的顺序组成,每一层由若干神经元组成。相邻两层之间的神经元通过参数(包括权重\(W\)和偏置\(b\))矩阵连接。神经元可以被激活,激活信号沿着参数矩阵逐层向后传递到输出层。这里,我们用\(\Theta^{(j)}_{k,i}\)表示连接第\(j\)层第\(i\)个神经元与\(j+1\)层第\(k\)个神经元的参数,\(a_i^{(j)}\)表示第\(j\)层中第\(i\)个激活单元。
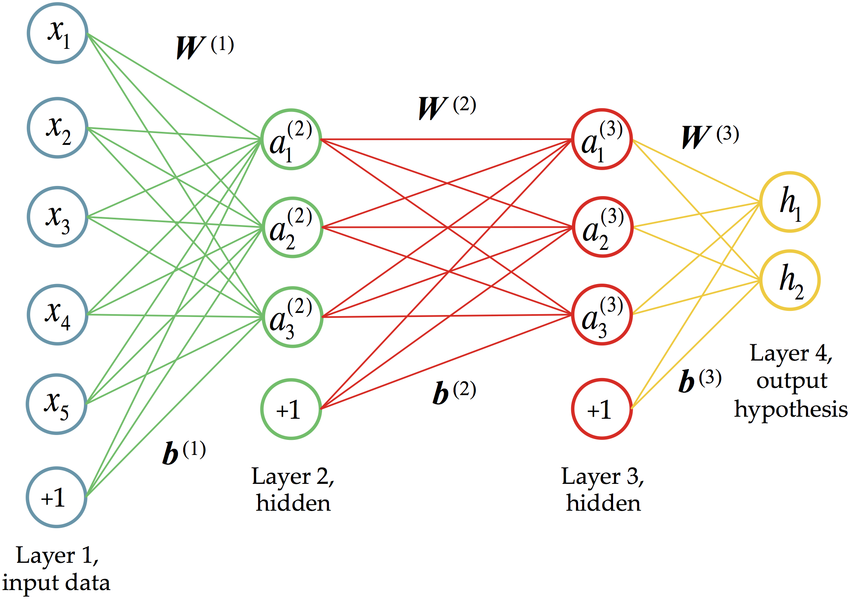
将输入值从输入层逐层传递到输入层的过程叫做前向传播(Forward Propagation),这也是神经网络模型进行预测的基础。考虑只有一个隐藏层的神经网络:
\[
\begin{bmatrix}x_0 \\x_1 \\ x_2 \\ x_3 \end{bmatrix}\rightarrow\begin{bmatrix}a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \\ \end{bmatrix}\rightarrow h_\theta(x)
\]
隐藏层中每个神经元的激活值为:
\[\begin{aligned} a_1^{(2)} &= g(\Theta_{1,0}^{(1)}x_0 + \Theta_{1,1}^{(1)}x_1 + \Theta_{1,2}^{(1)}x_2 + \Theta_{1,3}^{(1)}x_3) \\ a_2^{(2)} &= g(\Theta_{2,0}^{(1)}x_0 + \Theta_{2,1}^{(1)}x_1 + \Theta_{2,2}^{(1)}x_2 + \Theta_{2,3}^{(1)}x_3) \\ a_3^{(2)} &= g(\Theta_{3,0}^{(1)}x_0 + \Theta_{3,1}^{(1)}x_1 + \Theta_{3,2}^{(1)}x_2 + \Theta_{3,3}^{(1)}x_3) \end{aligned}\]
令
\[z_k^{(j+1)} = \Theta_{k,0}^{(j)}x_0 + \Theta_{k,1}^{(j)}x_1 + \cdots + \Theta_{k,d}^{(j)}x_d\]
则
\[\begin{aligned}a_1^{(2)} = g(z_1^{(2)}) \\ a_2^{(2)} = g(z_2^{(2)}) \\ a_3^{(2)} = g(z_3^{(2)}) \end{aligned}\]
那么
\[
\begin{aligned} h_\Theta(x) = a_1^{(3)} = g(\Theta_{1,0}^{(2)}a_0^{(2)} + \Theta_{1,1}^{(2)}a_1^{(2)} + \Theta_{1,2}^{(2)}a_2^{(2)} + \Theta_{1,3}^{(2)}a_3^{(2)}) \end{aligned}
\]
这样,我们就计算出了\(h_\Theta(x)\)的值,得到模型的预测结果。
上述过程推广到向量形式:
\[\begin{aligned}x = \begin{bmatrix}x_0 \\ x_1 \\ \vdots \\ x_d\end{bmatrix},\quad z^{(j)} = \begin{bmatrix}z_1^{(j)} \\ z_2^{(j)} \\ \vdots \\ z_{s_j}^{(j)}\end{bmatrix}, \quad a^{(j)} = \begin{bmatrix}a_1^{(j)} \\ a_2^{(j)} \\ \vdots \\ a_{s_j}^{(j)}\end{bmatrix}\end{aligned}\]
\[ \begin{aligned} z^{(j)} &= \Theta^{(j-1)}a^{(j-1)}\a^{(j)} &= g(z^{(j)})\z^{(j+1)} &= \Theta^{(j)}a^{(j)} \end{aligned} \]
注意,如果网络模型的第 \(j\)层有 \(s_j\)个神经元,而第\(j+1\)层有\(s_{j+1}\)个神经元,那么参数矩阵的维度(包含偏置项)为\(s_{j+1} \times (s_j + 1)\)。
标签:spl nim span 回归 一个 isp 学习 play math
原文地址:https://www.cnblogs.com/littleorange/p/12238331.html