标签：als 而不是 函数 span 打表 mamicode class type 公式
我们定义一种函数φ(x)，它的值为比x小的数里与x互质的数的个数。
其计算公式是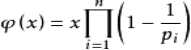 
(其中p1, p2……pn为x的所有质因数，x是不为0的整数)。
定义φ(1) = 1。
这个公式可以这样理解，对于整数x的任何一个素因子pi，在1-n中，它的倍数的个数为x/pi，剩下的数就是x*(1-1/pi)个。至于为什么用的连乘而不是连加，这个跟容斥有关系，有的数可能同时是多个素因子的乘积，可能被多次计算，在此不做证明。
求单个数的欧拉函数
typedef long long LL; LL eular(LL n) { LL ans = n; for(int i = 2;i*i<=n;++i) { if(n%i==0) { ans-=ans/i; while(n%i==0) n/=i; } } if(n>1) ans-=ans/n; return ans; }
欧拉函数打表
//线性筛（同时得到欧拉函数和素数表） const int maxn = 1e7; bool check[maxn+10]; int phi[maxn+10]; int prime[maxn+10]; int tot;//素数个数 void phi_and_prime_table(int N) { memset(check,false,sizeof(check)); phi[1] =1; tot =0; for(int i =2;i<=N;++i) { if(!check[i]) { prime[tot++] = i; phi[i] = i-1; } for(int j = 0;j<tot;++j) { if(i*prime[j]>N) break; check[i*prime[j]] = true; if(i%prime[j]==0) { phi[i*prime[j]] = phi[i]*prime[j]; break; } else phi[i * prime[j]] = phi[i] * (prime[j]-1); } } }
标签：als 而不是 函数 span 打表 mamicode class type 公式
原文地址：https://www.cnblogs.com/baihualiaoluan/p/12239084.html
