社团活动

bbq的工作是管理学校的社团活动，具体来说是为每个社团活动分配教室。要把有限的教室合理安排给这些社团，是不容易的。

每个社团活动用k, t1, t2来表示：该社团活动在第t1天～第t2天内需要k个教室（包括t1，t2）。

bbq总是按社团活动申请的先后顺序分配教室，如果某一天剩余的教室数量不够满足某社团的要求，则停止教室的分配。bbq需要告知该社团，他们的该次社团活动无法进行。

每组输入数据第一行包括两个正整数n、m，为总天数和社团活动的总数量。

第二行包含n个正整数，其中第i个数为r

，表示第i天空教室的数量。

接下来有m行，每行为一个社团活动的信息，包含三个正整数k, t₁, t_2。（k, t1, t2如题目描述）。

规定：

天数与社团活动编号均用从1开始的整数编号。

1≤n, m≤10

，0≤ri≤10

，0≤k≤109  ,1≤t1≤t2≤n。

如果所有社团的申请均可满足，则输出0。

否则输出一个正整数，为需要bbq告知的活动无法进行的社团活动编号。

4 3
2 5 4 3
2 1 3
3 2 4
4 2 4

2

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e6+50;
long long n,m;
long long a[N],room[N],t1[N],t2[N],sum[N];
int check(int mid){
    memset(sum,0,sizeof(sum));
    for(int i=1;i<=mid;i++){
        sum[t1[i]]-=room[i];
        sum[t2[i]+1]+=room[i];
    }
    int cnt=0;
    for(int i=1;i<=n;i++){
        cnt+=sum[i];
        if(a[i]+cnt<0)
            return 0;
    }
    return 1;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=m;i++){
        cin>>room[i]>>t1[i]>>t2[i];
    }
    int l=1,r=m+1;
    while(l<r){
        int mid=(l+r)>>1;
        if(check(mid))
            l=mid+1;
        else
            r=mid;    
    }
    if(l==m+1)
        cout<<0<<endl;
    else
        cout<<l<<endl;    
    return 0;
} 

View Code

首先要弄清楚这道题的意思，请多读几遍。

题的大意是说要给社团分配教室，但教室的总量是有限的，并且每天剩余的教室是不同的，说白了，这就是要对区间进行减法操作，拿题中给的样例来说，第一行中的4表示总天数是4，3表示社团活动的数量。第二行表示这四天中每天剩余教室的数量，接下来的3行表示社团活动的信息，包括需要的教室数量，和持续的天数。拿第一个社团活动信息来说，2 1 3 表示在第1到3天中，每天要用2个教室，这时候就把2 5 4 3中的2 5 4每个都减去2，

代表这些教室被占用了，这时候剩余教室的信息更新为    0 3 2 3然后看第二个社团活动信息 3 2 4 代表这个社团活动在第2到4天中，每天要用3个教室，这时候就把  0 3 2 3中的3 2 3每个都减去3，这时可以发现第三天剩余的教室是两个，不够减去3，这时，分配教室的活动就停止，bbq就报告说这个社团活动不能满足要求，然后程序就结束了，所以只要找到第一个让区间里出现负值的社团活动就行了。

这题涉及到的知识有二分答案和差分数组

先说下二分答案，当问题结果具有单调性时，就可以使用二分答案来解决，拿本题来说，如果第i个社团的要求没法满足，那么第i个社团以后的所有社团的要求都满足不了，这个仔细想想。那么我们只要找到第一个满足不了的社团活动就行了，那么就用二分答案，

 使用二分答案需要找到答案区间的最小值l和最大值r，然后用（l+r)>>1来表示mid，(l+r)>>1的意思是，(l+r)除以2的整数部分，然后呢还需要一个check函数，将mid传进这个函数里，这个函数来判断mid是否符合条件，二分答案中，check函数的书写是比较重要的，check函数也会因题目而异，二分答案的其他部分就可以模板化了

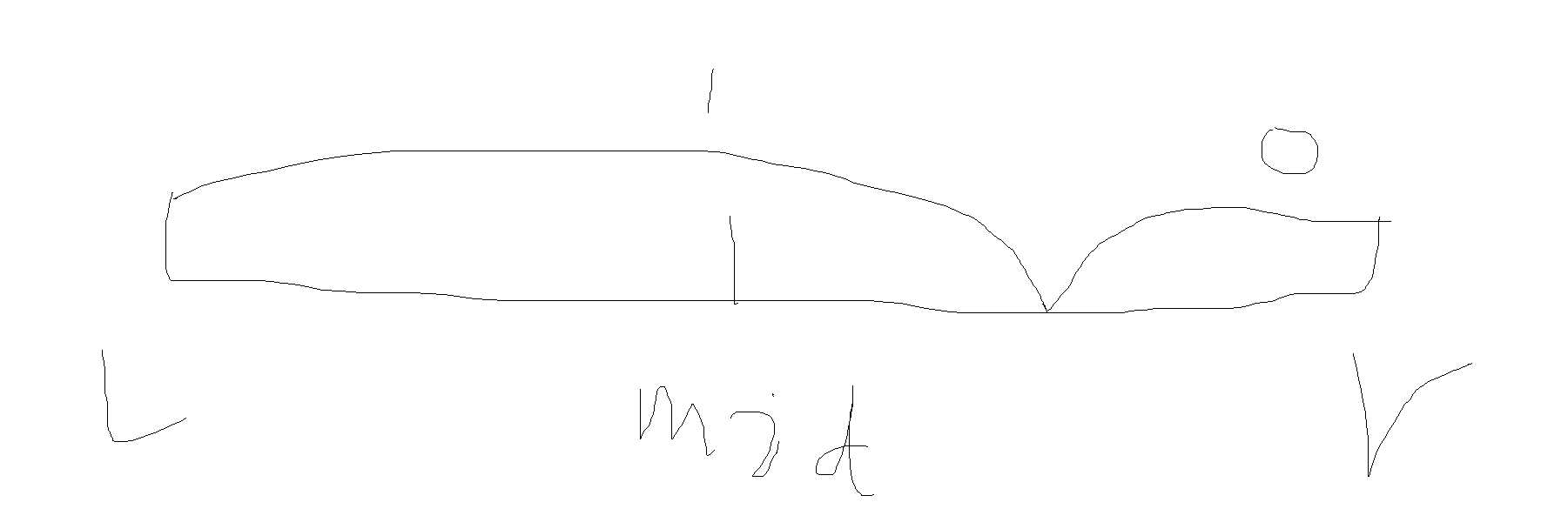
拿这道题来说，我们写的check函数是用来判断这个社团活动能不能被满足，如果mid所指的这个活动被满足了，（见上图，用1表示满足条件，0表示不满足条件），我们就l=mid+1,因为我们要找的是满足和不满足交界的地方,并且我们要找的是不满足的第一个活动，mid+1可能被满足，也可能不被满足。

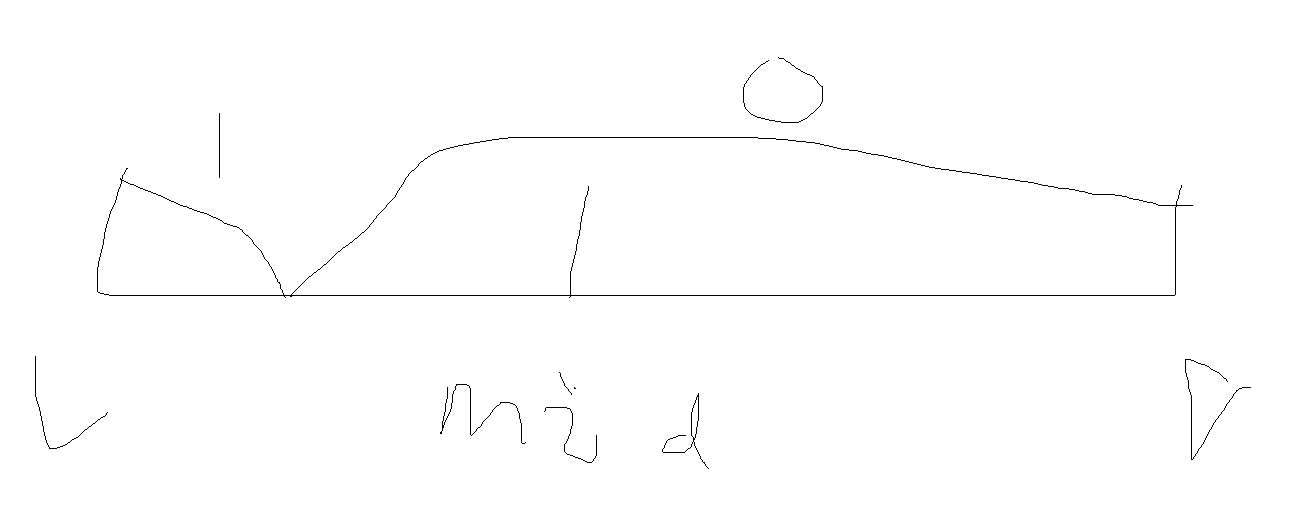
 如果mid所指的活动没有被满足（如上图），我们就r=mid，这时候就要改变右边界的界限，注意，因为mid是不被满足的，而我们要找的就是不被满足的，所以我们不能丢掉mid，如果用r=mid-1，那就错了。

就这样不停的缩小范围，到最后l=r的时候，结束二分。

在这里解释一下代码中为何r=m+1,社团活动的编号不是到m就结束了吗，那么答案的范围就应该到m啊，为什么还要加1呢，这是因为还有另一种情况，那就是所有的社团活动都被满足了，所以我们用m+1来表示这种情况，也就是说答案的范围是1到m+1而不是1到m。

在check函数的书写上，这里用了差分数组的性质。先解释一下什么叫做差分数组。

假如说有两个数组a和b，如果b[i]=a[i]-a[i-1],那么b数组就叫做a数组的差分数组。

比如说有一个数组a;1 3 3 4 2 5 6 7 4

差分之后的数组b为;1 2 0 1 -2 3 1 1 -3

数组b有一个特性，那就是数组b累加起来后的值（b[0]+b[1]+`````+b[i])等于a[i]的值,

差分数组在应对区间加减法上很好用，拿本题样例来说，把2，5，4，3存进数组a[1]到a[4]中，