标签:img code lin als 评估 技术 btn 识别 developer
目录
准确率是指我们的模型预测正确的结果所占的比例。
正式点说,准确率的定义如下:
$Accuracy = \frac{Number of correct predictions}{Total number of predictions}$
对于二元分类,也可以根据正类别和负类别按如下方式计算准确率:
$Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$
其中,TP = 真正例,TN = 真负例,FP = 假正例,FN = 假负例。
例如:该模型将 100 条流分为Tor (正类别)或no-Tor(负类别):
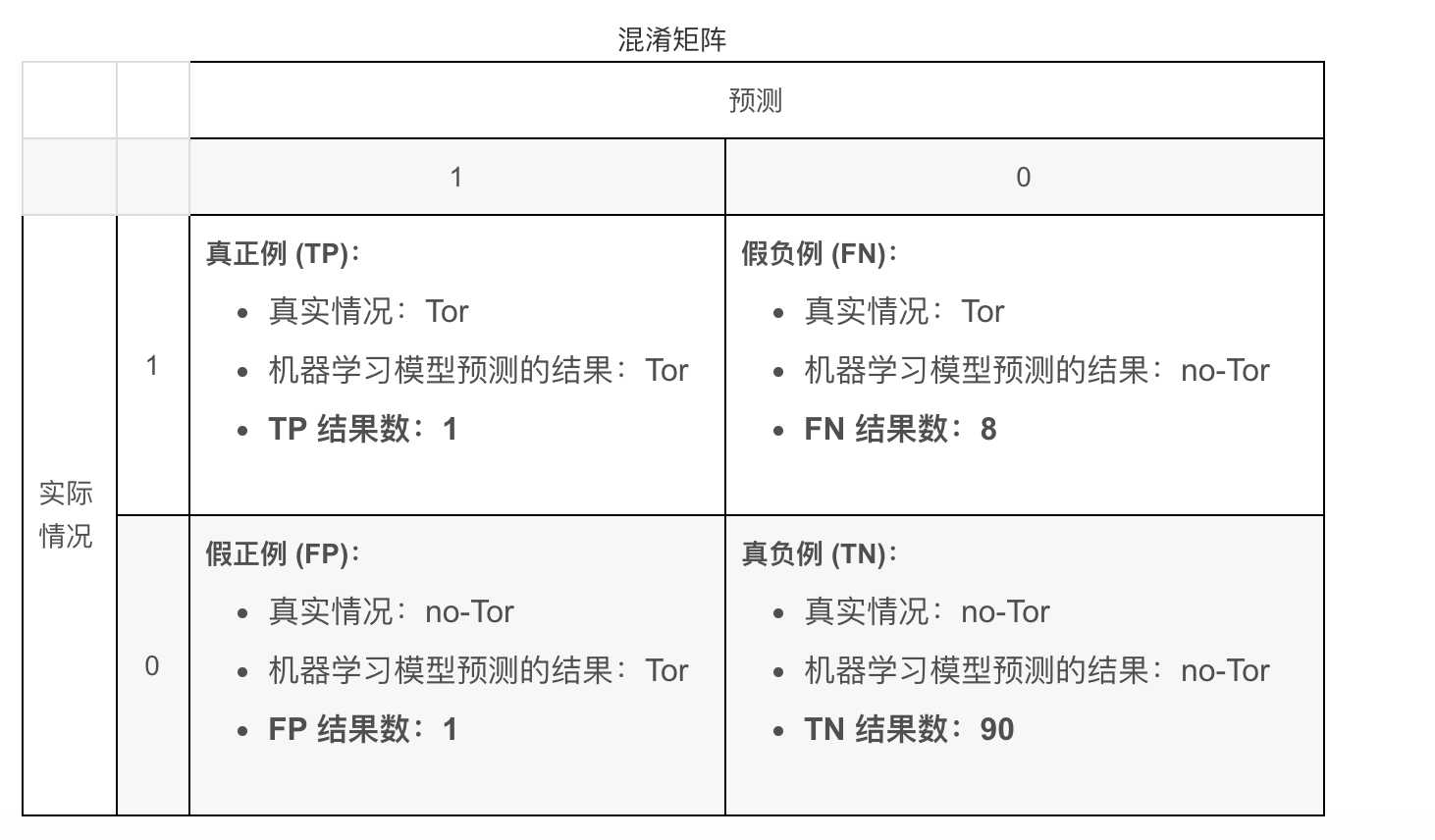
$Accuracy = \frac{TP+TN}{TP+TN+FP+FN}= \frac{1+90}{1+90+1+8}=0.91$
准确率为 0.91,即 91%(总共 100 个样本中有 91 个预测正确)。
但仔细琢磨正负例的比例,显然是不够能说明问题的。例如,我有1000个样本,其中910都是负例,模型只要学到将所有样本预测为负例,准确率即可达到91%,这样却永远检测不出正例。
所以,当使用分类不平衡的数据集(比如正类别标签和负类别标签的数量之间存在明显差异)时,单单准确率一项并不能反映全面情况。
在2、3部分中,我们将介绍两个能够更好地评估分类不平衡问题的指标:召回率和精确率。
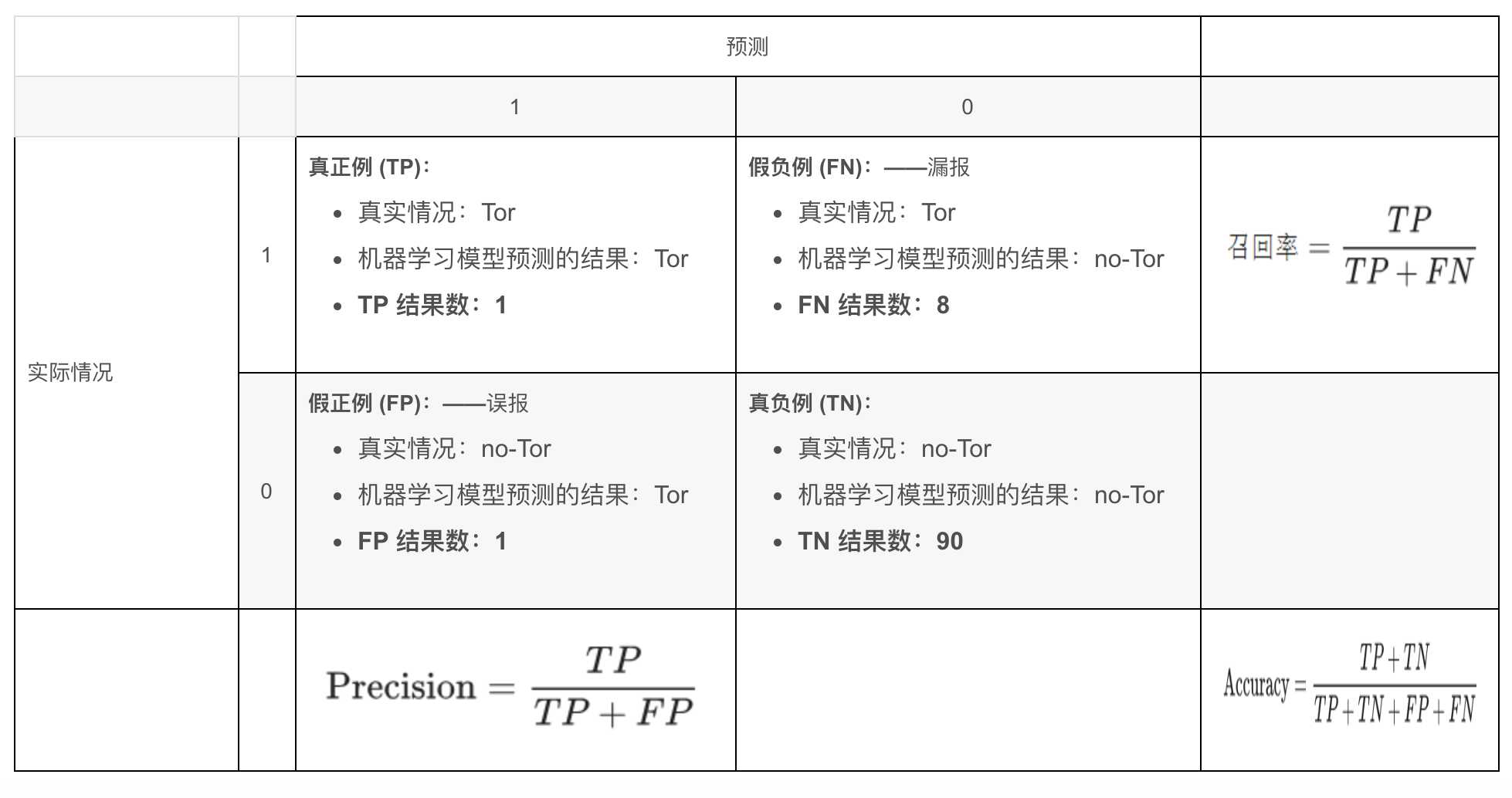
召回率表示在所有正类别样本中,被正确识别为正类别的比例。
从数学上讲,召回率的定义如下:
$Recall=\frac{TP}{TP+FN}$
让我们来计算一下流量分类器的召回率(上面的例子):
$Recall=\frac{TP}{TP+FN} = \frac{1}{1+8} = 0.11$
该模型的召回率是 0.11,也就是说,该模型能够正确识别出所有Tor流量的百分比是 11%。
精确率表示被识别为正类别的样本中,确实为正类别的比例。
精确率的定义如下:
$Precision=\frac{TP}{TP+FN}$
让我们来计算一下流量分类器(上面的例子)的精确率:
$Precision=\frac{TP}{TP+FN} =\frac{1}{1+1} = 0.5$
该模型的精确率为 0.5,也就是说,该模型在预测Tor流量方面的正确率是 50%。
参考:https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall?hl=zh-cn
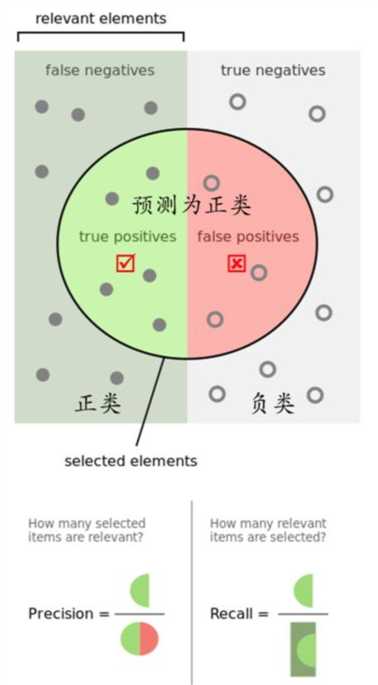
在信息检索领域,召回率和精确率又被称为查全率和查准率:
由此可以理解:
参考:机器学习性能评估指标
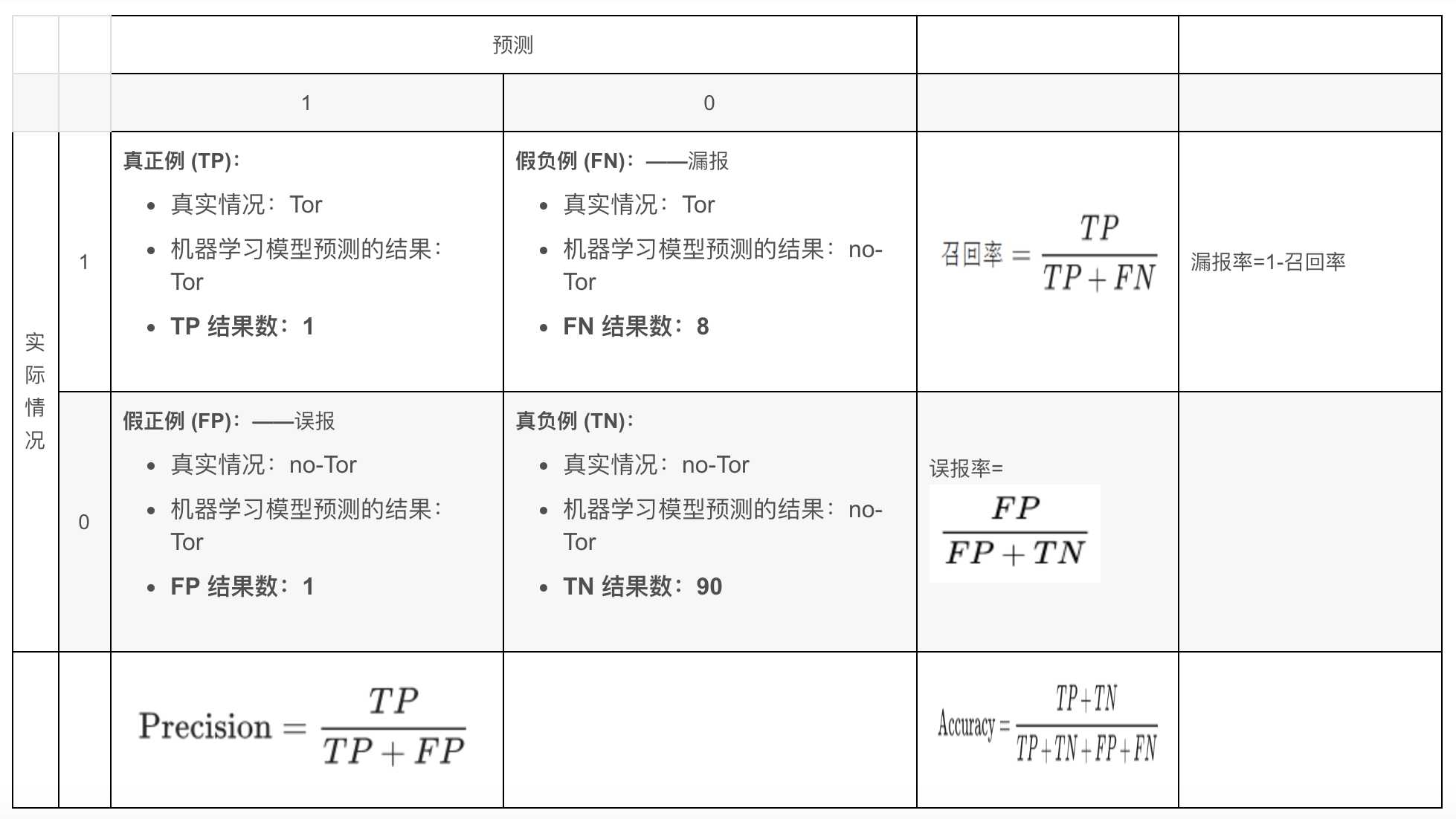
真正例率 TPR = TP / (TP + TN)
表示,被挑出来的(预测是“正”的),且正确的(预测值=真实值)的,占总的预测正确的比率。
反正例率 FPR = FP / (FP + TN)
表示,被挑出来的(预测是“正”的),但错误的(预测值!=真实值)的,占总的预测错误的比率。
TPR越大,则表示挑出的越有可能(是正确的);FPR越大,则表示越不可能(在挑选过程中,再挑新的出来,即再挑认为是正确的出来,越有可能挑的是错误的)。
TNR(True Negative Rate)可以理解为所有反类中,有多少被预测成反类(反类预测正确),给出定义如下:
FNR(False Negative Rate)可以理解为所有正类中,有多少被预测成反类(反类预测错误),给出定义如下:
误报率(FPR)、漏报率(FNR)
标签:img code lin als 评估 技术 btn 识别 developer
原文地址:https://www.cnblogs.com/shona/p/12239400.html