标签:center 一个 快速幂 int() 流程 strong 斐波那契数 延伸 src
首先,矩阵快速幂是从快速幂里延伸出的算法,需要快速幂以及线性代数的知识。快速幂是利用二进制的有关性质快速计算出xn,矩阵快速幂则是通过将递推式化成一个矩阵,求解某个递推结果的过程变成求解一个矩阵的n次幂的过程,从而能用快速幂加快递推式的求解。
举个例子,我们来用斐波那契数列来解释一下矩阵快速幂的具体流程。大家都知道递推式为F(n) = F(n-1)+F(n-2)。这个式子十分浅显易懂,但是用来及求解较大的项时就会变得非常慢,因此我们可以考虑用矩阵快速幂来优化一下计算过程。在一般情况下,我们要通过递推式获得一个矩阵之间的递推关系,形如T*A(n-1) = A(n)(其中T,A(n-1),A(n)均为矩阵)。
对于F(n),我们可以得到一个矩阵之间的递推关系就是
其中,要注意的是,为了方便运算,我们构造的矩阵都是方阵,在这里An其实也是一个2*2的方阵,但我们只关心An的左边,所以就没有写出An的右边。很明显,上面给出的等式是成立的,接下来,如果我们要求F(n),就可以先求出A(n) = Tn-2*A(1),
A(1)是左边为两个1的2*2矩阵,此时F(n)就是A(n)左上角的值。这样,我们就把一个递推式的计算过程优化,然后运用矩阵快速幂进行极快的求解。
矩阵快速幂的难点就在于矩阵的构造。
下面给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c;(a,b,c是常数)
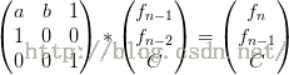
2.f(n)=c^n-f(n-1) ;(c是常数)
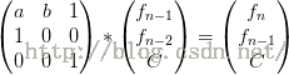
const int N = 2; const int mod = 10000; struct Matrix { int mat[N][N]; Matrix(){}; Matrix operator*(Matrix const &b) const { Matrix res; memset(res.mat,0,sizeof(res.mat)); for(int i = 0;i<N;++i) { for(int j = 0;j<N;++j) { for(int k = 0;k<N;++k) { printf("%d %d %d\n",i,j,k); res.mat[i][j] = (res.mat[i][j]+this->mat[i][k]*b.mat[k][j])%mod; } } } return res; } void Print() { for(int i =0;i<N;++i) { for(int j = 0;j<N;++j) printf("%d ",mat[i][j]); printf("\n"); } return ; } }; Matrix pow_mod(Matrix base,int n) { Matrix res; memset(res.mat,0,sizeof(res.mat)); for(int i = 0;i<N;++i) res.mat[i][i] = 1; while(n>0) { if(n&1) { res.Print(); res= res*base; } base = base*base; n>>=1; res.Print(); } return res; }
标签:center 一个 快速幂 int() 流程 strong 斐波那契数 延伸 src
原文地址:https://www.cnblogs.com/baihualiaoluan/p/12239349.html