LeetCode 42 接雨水

标签：++   节省空间   多少   --   ext   高度图   return   i+1   cto   

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

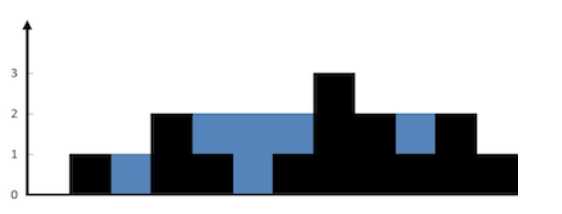
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

法一（按列动态规划）

首先容易想到的是遍历数组一列一列求的方法，简单来说就是在遍历时求出每一列左右两个最大高度，取小者和所在列的高度比较（若大于所在列高度，为凹字型，可接水；反之为凸字型，不可接）
但是在每次遍历的同时再次遍历求左右最大，复杂度较高。考虑在遍历前，利用状态转移方程先将左右情况求出。

代码

class Solution {
public:
    int trap(vector<int>& height) {
        int sum=0;
        int n=height.size();
        vector<int> Lmax(n,0);
        vector<int> Rmax(n,0);
        for(int i=0;i<n-1;i++){
            Lmax[i+1]=max(height[i],Lmax[i]);//左
        }
        for(int i=n-1;i>=1;i--){
            Rmax[i-1]=max(height[i],Rmax[i]);//右
        }
        for(int i=1;i<n-1;i++){
            int k=min(Lmax[i],Rmax[i])-height[i];
            if(k>0){//凹字，计算接水值
                sum+=k;
            }
        }
        return sum;
    }
};

法二（双指针）

在法一基础上取消数组Rmax和Lmax，利用左右指针节省空间。

代码

class Solution {
public:
    int trap(vector<int>& height) {
        int Lmax=0,Rmax=0,sum=0;
        int left=1,right=height.size()-2;
        if(height.size()<3)return 0;//不加过不了
        int n=1;
        while(n<=height.size()-2){//循环n-2次
            if(height[left-1]<height[right+1]){
                Lmax=max(Lmax,height[left-1]);//若左小于右，由于Lmax是由height演化而来，左侧最大一定小于右侧，直接将左侧和所在列比较
                if(Lmax>height[left])sum+=Lmax-height[left];
                left++;
            }
            else{
                Rmax=max(Rmax,height[right+1]);
                if(Rmax>height[right])sum+=Rmax-height[right];//同理，若左大于等于右，左侧最大一定大于等于右侧
                right--;
            }
            n++;
        }
        return sum;
    }
};

法三（括号法）

遍历数组，将第一个数压栈，指针next指向后一个数，比较两数大小，若height[next]>栈顶数（意味着一个右括号），弹出栈顶元素，计算接水值；若<=（左括号），压栈，直到遍历结束。

代码

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> s;
        int next=0;
        int dis,sum=0;
        while(next<height.size()){
            while(!s.empty()&&height[next]>height[s.top()]){//出现右括号
                int H=height[s.top()];//保存栈顶数，用于后面计算差值
                s.pop();//弹出左括号
                if(s.empty())break;//只有右括号无左括号情况退出
                dis=next-s.top()-1;//计算距离
                sum+=dis*(min(height[s.top()],height[next])-H);//取小者，木桶效应
            }
            s.push(next);//若next小，出现左括号，则压栈
            next++;
        }
        return sum;
    }
};

LeetCode 42 接雨水

标签：++   节省空间   多少   --   ext   高度图   return   i+1   cto   

原文地址：https://www.cnblogs.com/ambassdor/p/12244807.html