标签:main函数 https out 好的 clu 为我 题解 load 十分
这道题是一道dfs好题,很多人在题解里用了各种剪枝,以及一些奇奇怪怪的优化,还有大佬用的舞蹈链算法,蒟蒻不会舞蹈链,剪枝的效果也不是很好,只能用一些优化来过这道题了。
这道题虽然已经有很多题解了,但是我还是来交题解的原因是我觉得我的代码跑的,可以给大家提供一些关于搜索顺序的思路,~~希望管理员不要认为我这是重复的解法~~。不过我敢保证,我的代码跑的一定比除了打表题解以外的题解跑的快。
~~说实话,这题普通剪枝也可以水过~~,但是既然我们要追求速度,就不能仅仅局限于最优性、可行性剪枝。画了几张图以后发现一个规律,先搜索约束个数多的点,效率最高。这里的约束个数,就是这个点所在行、列、宫已经填好的数的个数之和。(具体内容见下图)
所以我们就得到了一个思路,与处理好搜索顺序,也就是统计每个点的约束个数,先找到最多的,然后记录下来,假设它已经填好(把他所在的行、列、宫的约束个数加一),然后继续找第二多的就好了。最后按照这个顺序在每次dfs结束后找到下一个填数的点,就ok了,这样可以达到总效率888ms,已经非常快了。
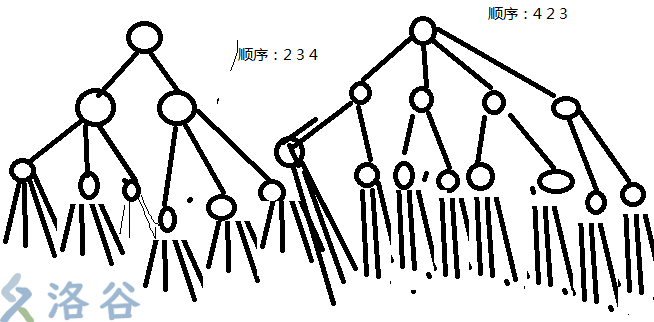
显然先搜索可能性为2的节点比先搜索可能性为4的搜索树小很多,当可能性扩大到9*9=81时,差距会十分明显,效率自然也就高很多了
很多细节详见代码注释。
因为很多人只是预处理了列,按照列每次处理9个,所以效率没有我这种写法高
#include<iostream>
#include<algorithm>
using namespace std;
int ans[13][13];
int cntc[13],cntr[13],cntb[13];
int belong(int x,int y){//判断x,y属于哪一个宫
int h,l;
if(x<=3)h=1;
else if(x<=6)h=2;
else h=3;
if(y<=3)l=1;
else if(y<=6)l=2;
else l=3;
return (h-1)*3+l;
}
pair<int,int> s[100];
int cnt=0;
int ANS=0;
int v[10][10]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6,},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
//记录每一个点的分数
void calc(){
int tot=0;
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++)
tot+=ans[i][j]*v[i][j];
ANS=max(ANS,tot);
}//搜索完成后计算答案的函数
int col[20][20],row[20][20],block[20][20];
void dfs(int x,int y,int now){//简单的搜索,按照我们在main函数中预处理的pair<int,int> s的顺序搜索,这样效率最高
if(now==cnt+1)calc();
int b=belong(x,y);
for(int i=1;i<=9;i++){
if(!col[x][i]&&!row[y][i]&&!block[b][i]){//判断是不是可行
col[x][i]=row[y][i]=block[b][i]=1;//标记访问
ans[x][y]=i;
dfs(s[now+1].first,s[now+1].second,now+1);
col[x][i]=row[y][i]=block[b][i]=ans[x][y]=0;//回溯
}
}
}
int vis[20][20];
int main(){
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++){
cin>>ans[i][j];
if(ans[i][j]!=0)vis[i][j]=1,cntc[i]++,cntr[j]++,cntb[belong(i,j)]++,col[i][ans[i][j]]=1,row[j][ans[i][j]]=1,block[belong(i,j)][ans[i][j]]=1;
else cnt++;
}//这里为预处理每一个点在行、列、宫中的限制个数
for(int k=1;k<=cnt;k++){
int Max=0,px,py;
for(int i=1;i<=9;i++
for(int j=1;j<=9;j++)
if(cntc[i]+cntr[j]+cntb[belong(i,j)]>Max&&!vis[i][j])
Max=cntc[i]+cntr[j]+cntb[belong(i,j)],px=i,py=j;
s[k]=make_pair(px,py);
//找到可能性最少的点,并假设他已经填好,继续找下一个
cntc[px]++,cntr[py]++,cntb[belong(px,py)]++;
vis[px][py]=1;
// cout<<k<<" "<<px<<" "<<py<<endl;
}
dfs(s[1].first,s[1].second,1);//从第一个开始搜索
if(ANS!=0)
cout<<ANS<<endl;
else cout<<-1<<endl;//输出答案
}
标签:main函数 https out 好的 clu 为我 题解 load 十分
原文地址:https://www.cnblogs.com/wo-bu-yao-bao-ling/p/12245427.html