标签:otto als namespace cout string class struct 截图 media
(一)BFS
1.地牢大师
你现在被困在一个三维地牢中,需要找到最快脱离的出路!
地牢由若干个单位立方体组成,其中部分不含岩石障碍可以直接通过,部分包含岩石障碍无法通过。
向北,向南,向东,向西,向上或向下移动一个单元距离均需要一分钟。
你不能沿对角线移动,迷宫边界都是坚硬的岩石,你不能走出边界范围。
请问,你有可能逃脱吗?
如果可以,需要多长时间?
输入格式
输入包含多组测试数据。
每组数据第一行包含三个整数 L,R,C 分别表示地牢层数,以及每一层地牢的行数和列数。
接下来是 L 个 R 行 C 列的字符矩阵,用来表示每一层地牢的具体状况。
每个字符用来描述一个地牢单元的具体状况。
其中, 充满岩石障碍的单元格用”#”表示,不含障碍的空单元格用”.”表示,你的起始位置用”S”表示,终点用”E”表示。
每一个字符矩阵后面都会包含一个空行。
当输入一行为”0 0 0”时,表示输入终止。
输出格式
每组数据输出一个结果,每个结果占一行。
如果能够逃脱地牢,则输出”Escaped in x minute(s).”,其中X为逃脱所需最短时间。
如果不能逃脱地牢,则输出”Trapped!”。
数据范围
1≤L,R,C≤100
输入样例:
3 4 5
S....
.
输出样例:
Escaped in 11 minute(s).
Trapped!
解题思路:一道三维的BFS搜索题,我们可以建立三个移动数组:vx,vy,vk,分别表示北,南,东,西,上,下,设置一个三维的map数组来存储地图,
设置一个vis数组,用来判断是否走过以及距离。
代码:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=110;
int l,r,c;
char map[N][N][N];
int vis[N][N][N];
int vx[]={1,-1,0,0,0,0};
int vy[]={0,0,1,-1,0,0};
int vk[]={0,0,0,0,1,-1};
typedef struct Node
{
int k,x,y;
};
bool check(int K,int X,int Y)
{
if(X<0||X>=r||Y<0||Y>=c||K<0||K>=l)
return false;
if(map[K][X][Y]==‘#‘)
return false;
if(vis[K][X][Y]!=0)
return false;
return true;
}
int bfs(Node start)
{
queue<Node> q;
memset(vis,0,sizeof(vis));
q.push(start);
while(!q.empty())
{
Node tem=q.front();
if(map[tem.k][tem.x][tem.y]==‘E‘)
return vis[tem.k][tem.x][tem.y];
q.pop();
for(int i=0;i<6;i++)
{
int X=tem.x+vx[i];
int Y=tem.y+vy[i];
int K=tem.k+vk[i];
if(check(K,X,Y)==false)
continue;
vis[K][X][Y]=vis[tem.k][tem.x][tem.y]+1;
Node t={K,X,Y};
q.push(t);
}
}
return 0;
}
int main()
{
int i,j,bx,by,bk,k;
Node start;
string ss;
while(1)
{
cin>>l>>r>>c;
if(l==0&&r==0&&c==0)
break;
for(k=0;k<l;k++)
{
for(i=0;i<r;i++)
{
for(j=0;j<c;j++)
{
cin>>map[k][i][j];
if(map[k][i][j]==‘S‘)
{
bk=k,bx=i,by=j;
start={bk,bx,by};
}
}
}
getline(cin,ss);
}
int ans=bfs(start);
if(ans)
cout<<"Escaped in "<<ans<<" minute(s)."<<endl;
else
cout<<"Trapped!"<<endl;
}
return 0;
}
2.全球变暖
你有一张某海域 N×N 像素的照片,”.”表示海洋、”#”表示陆地,如下所示:
.......
.
其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿,例如上图就有 2 座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
输入格式
第一行包含一个整数N。
以下 N 行 N 列,包含一个由字符”#”和”.”构成的 N×N 字符矩阵,代表一张海域照片,”#”表示陆地,”.”表示海洋。
照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。
输出格式
一个整数表示答案。
数据范围
1≤N≤1000
输入样例1:
7
.......
.
输出样例1:
1
输入样例2:
9
.........
.
输出样例2:
1
解题思路:该题要找出完全被淹没的岛屿的个数,首先我们要做的是找出所有的联通快,我们可以用bfs来找,对于每一个联通快我们需要判断他是否被完全淹没,如何判断呢?
我们可以找出该联通块里一共有多少个像素,再找出有多少个像素与海相邻,如果两者的个数相等,那么该岛屿必然会被完全淹没。
否则,不会完全淹没。特别注意:当你用bfs开始寻找时,此时的像素总数的初始值为1.
代码:
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
const int N=1010;
char map[N][N];
bool ts[N][N];
int vx[]={1,-1,0,0};
int vy[]={0,0,1,-1};
int ans,n;
typedef struct Node
{
int x,y;
};
bool check(int X,int Y)
{
if(X<0||X>=n||Y<0||Y>=n)
return false;
if(map[X][Y]==‘.‘)
return false;
if(ts[X][Y]==true)
return false;
return true;
}
void bfs(int i,int j)
{
Node start={i,j};
queue<Node> q;
ts[i][j]=true;
q.push(start);
int total=1,ver=0;
while(q.size())
{
Node t=q.front();
q.pop();
int flag=false;
for(i=0;i<4;i++)
{
int X=t.x+vx[i];
int Y=t.y+vy[i];
if(X>=0&&X<n&&Y>=0&&Y<n&&map[X][Y]==‘.‘)
{
flag=true;
}
if(check(X,Y)==false)
continue;
total++;
ts[X][Y]=true;
Node f={X,Y};
q.push(f);
}
if(flag)
ver++;
}
if(total==ver)
ans++;
}
int main()
{
int i,j;
cin>>n;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
cin>>map[i][j];
}
}
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if(!ts[i][j]&&map[i][j]==‘#‘)
{
bfs(i,j);
}
}
}
cout<<ans;
return 0;
}
3.完全二叉树的权值
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 A1,A2,⋅⋅⋅AN,如下图所示:
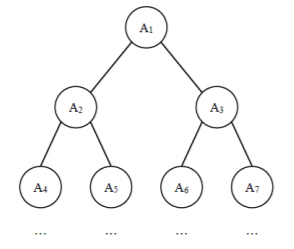
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?
如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。
输出格式
输出一个整数代表答案。
数据范围
1≤N≤105,
−105≤Ai≤105
输入样例:
7
1 6 5 4 3 2 1
输出样例:
2
解题思路:每一层的个数都是=2n-1个,而且开头的下标都是2的倍数
代码:
#include<iostream>
using namespace std;
const int N=100010;
typedef long long ll;
ll a[N];
ll maxn,sum,ans;
int main()
{
ll i,j,n,k;
cin>>n;
for(i=1;i<=n;i++)
cin>>a[i];
maxn=a[1];
ans=1;
k=1;
for(i=2;i<=n;i=i*2)
{
sum=0;
for(j=i;j<=i*2-1&&j<=n;j++)
{
sum+=a[j];
}
k++;
if(sum>maxn)
{
maxn=sum;
ans=k;
}
}
cout<<ans;
return 0;
}
双指针,BFS和图论(二)
标签:otto als namespace cout string class struct 截图 media
原文地址:https://www.cnblogs.com/xiaofengzai/p/12245991.html

