标签:辅导 lock des document 文字 必须 cal inf 注意
1、寒假下发的三套试题的答案已经上传,地址:地址;
2、为便于大家的网上学习,特开设博文用于收集大家的问题,博文地址:地址;
3、从第二次开始准备自己使用录屏软件在家录制;如果制作顺利,视频地址还会放在这一博文里面,请大家关注;
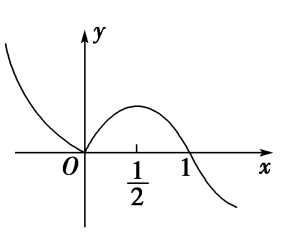
分析:由图可知,外函数\(f(x)\)在区间\((-\infty,0)\)和\([\cfrac{1}{2},+\infty)\)上单调递减,在区间\([0,\cfrac{1}{2}]\)上单调递增,
又\(0<a<1\)时,内函数\(y=log_ax\)在区间\((0,+\infty)\)上单调递减,
故要使得复合函数函数\(g(x)=f(log_ax)(0<a<1)\)单调递减,
则需要\(log_ax\in [0,\cfrac{1}{2}]\),即\(0\leq log_ax\leq \cfrac{1}{2}\),
解得\(x\in [\sqrt{a},1]\),故选\(B\)。
分析:\(f(x)=\cfrac{2018^{x+1}+2016}{2018^x+1}=\cfrac{2018^x\cdot 2018+2016}{2018^x+1}=\cfrac{2018(2018^x+1)-2}{2018^x+1}=2018-\cfrac{2}{2018^x+1}\)
故函数\(f(x)\)在区间\([-a,a]\)上单调递增,故\(M=f(x)_{max}=f(a)\),\(N=f(x)_{min}=f(-a)\),
故\(M+N=f(a)+f(-a)=2018-\cfrac{2}{2018^a+1}+2018-\cfrac{2}{2018^{-a}+1}=4036-2=4034\),故选\(D\).
分析:由定义的运算可知\(2\otimes x=\sqrt{2^2-x^2}=\sqrt{4-x^2}\),\(x\oplus 2=\sqrt{(x-2)^2}=|x-2|\),
于是\(f(x)=\cfrac{\sqrt{4-x^2}}{2-|x-2|}\),仿例2先求得定义域为\([-2,0)\cup(0,2]\),
故\(f(x)=\cfrac{\sqrt{4-x^2}}{2-(2-x)}=\cfrac{\sqrt{4-x^2}}{x}\),满足\(f(-x)=-f(x)\),故函数\(f(x)\)为奇函数。
反思:研究函数的性质,一般都要求定义域优先原则。
分析:函数\(f(x)\)满足条件,\(f(-x)+f(x)=0\),故为奇函数,又函数在\(R\)上单调递增,故由\(a\ge -b\),得到\(f(a)\ge f(-b)\),即\(f(a)\ge -f(b)\),则\(f(a)+f(b)\ge 0\),故选\(B\)。
【法1】:由函数\(f(x)\)为奇函数,则满足\(f(-x)=-f(x)\),
\(f(x)=\cfrac{x}{(2x+1)(x-a)}=\cfrac{x}{2x^2+(1-2a)x-a}\),
\(f(-x)=\cfrac{-x}{(-2x+1)(-x-a)}=\cfrac{-x}{2x^2-(1-2a)x-a}\),
则\(\cfrac{-x}{2x^2-(1-2a)x-a}=\cfrac{-x}{2x^2+(1-2a)x-a}\)应该恒成立,
只需要\(-(1-2a)=1-2a\),解得\(a=\cfrac{1}{2}\);故选\(A\);
【法2】:由于定义域中有\(-1,1\),故必然满足\(f(-1)=-f(1)\),解得\(a=\cfrac{1}{2}\);故选\(A\);和法1相比,是特值验证。
【法3】:由于奇函数的定义域关于原点对称,令\(2x+1=0\)得到\(x=-\cfrac{1}{2}\),故可知定义域中没有\(x=-\cfrac{1}{2}\);
令\(x-a=0\)得到\(x=a\),故定义域中必然没有\(x=a\),故\(a=\cfrac{1}{2}\);故选\(A\);
【法4】:\(f(x)=\cfrac{x}{(2x+1)(x-a)}=\cfrac{x}{2x^2+(1-2a)x-a}\),由于分子函数为奇函数,要是\(f(x)\)为奇函数,则分母函数\(y=2x^2+(1-2a)x-a\)为二次函数,
要是偶函数,则\(1-2a=0\),解得\(a=\cfrac{1}{2}\);故选\(A\);
分析:由题目可知,\(\begin{cases} &3-a>0 ① \\ &a>1 ②\\ &(3-a)7-3\leq a^{7-6}③\end{cases}\);即\(\begin{cases}&a<3 \\ &a>1 \\ &a\ge \cfrac{9}{4}\end{cases}\)
解得:\(a\in[\cfrac{9}{4},3)\);
反思:1、本题目常犯的错误是缺少第三条的限制;学生常认为函数在两段上分别单调递增,则在整体定义域\(R\)上一定单调递增,这个认知是错误的。原因是前者是后者的必要不充分条件。
2、防错秘籍:既要保证每段上的单调性,还要保证转折点处的单调性。
分析:由题目可知,\(\begin{cases} & 3-a>0 ① \\ &a>1 ②\\ &(3-a)7-3<a^{8-6}③\end{cases}\),解得:\(a\in(2,3)\);
反思:本题目和上例非常类似,但是又不一样,原因是数列是特殊的函数,所以在③中不等式的两端的自变量的取值不一样,而且不能取等号。
分析:先做出分段函数的第二段,当做第一段时,会考虑斜率\(1-a\),
当做射线\(y=(1-a)x+2a(x<1)\)的图像时,\(1-a\leq 0\)都不符合题意,只有\(1-a>0\)才有可能符合题意。
由于要求函数的值域为R,故要求分段函数的两段图像在\(y\)轴上的射影要占满\(y\)轴,
然后将其转化为文字语言,即左端函数的最大值必须大于或等于右端函数的最小值,
再转化为数学语言,即\((1-a)\cdot 1+2a\ge ln1\),
即需要满足\(\begin{cases}1-a>0\\(1-a)\cdot 1+2a\ge ln1\end{cases}\),
解得\(-1\leq a<1\);即\(a\in[-1,1)\)。
说明:注意三种数学语言的顺利转化。
分析:本题目属于求解分段函数方程,可以将\(f(x)\)这个整体视为已知中的\(x\),则原分段函数方程等价于
第一种情形,\(0\leq f(x)\leq 1\)且\(f(x)=1\);或第二种情形,\(f(x)-3=1\)且\(f(x)\notin[0,1]\),
其中第一种可化简为\(0\leq f(x)\leq 1\),再等价转化为\(\begin{cases}x\in[0,1]\\f(x)=1\end{cases}\)或\(\begin{cases}x\notin[0,1]\\0\leq x-3\leq 1\end{cases}\)
解得\(0\leq x\leq 1\)或\(3\leq x\leq 4\);
第二种可化简为\(f(x)=4\),再等价转化为\(\begin{cases}x\in[0,1]\\1=4\end{cases}\)或\(\begin{cases}x\notin[0,1]\\x-3=4\end{cases}\),解得\(x=7\);
综上所述,\(x\)的取值范围是\([0,1]\cup[3,4]\cup\{7\}\),故选\(D\)。
分析:令\(g(x)=(a^2-3a)x\),由于\(g(x)>0\)在区间\((-\infty,0)\)上要恒成立,
则有\(a^2-3a<0\),这样内函数\(g(x)\)只能单调递减,复合函数\(f(x)=log_{3a}g(x)\)是单调递减的,
所以外函数必须是单调递增的,故\(3a>1\),由\(\begin{cases}a^2-3a<0\\3a>1\end{cases}\),
解得\(\cfrac{1}{3}<a<3\),故\(a\in(\cfrac{1}{3},3)\)。
分析:由偶函数可知,\(f(x)\)总满足\(f(x)=f(-x)=f(|x|)\),\(f(x)\)在区间\((0,+\infty)\)上单调递减,
故将已知条件转化为\(f(2^{|a-1|})>f(|-\sqrt{2}|)=f(\sqrt{2})\),
利用在区间\((0,+\infty)\)上单调递减得到\(2^{|a-1|}<2^{\frac{1}{2}}\),则有\(|a-1|<\cfrac{1}{2}\),
解得\(a\in (\cfrac{1}{2},\cfrac{3}{2})\),故选\(C\).
\(2^{n+2}-(2n+1)\cdot 2^{n+1}=2\cdot 2^{n+1}-(2n+1)\cdot 2^{n+1}=(1-2n)\cdot 2^{n+1}\)
应用层次二:为整体换元和化简、计算做准备。
法1:\(8^{a+c-2b}=\frac{8^a\cdot 8^c}{8^{2b}}=\frac{(2^a)^3\cdot 8^c}{2^{2b}\cdot (4^b)^2}=\frac{189}{125}\);
法2:\(a=log_23\),\(b=log_45\),\(c=log_87\),
则\(8^{a+c-2b}=\frac{8^a\cdot 8^c}{8^{2b}}=\frac{(2^3)^{log_23}\cdot 8^c}{(8^b)^2}=\frac{3^3\times 7}{[(2^3)^{\frac{1}{2}log_25}]^2}\)
\(=\frac{3^3\times 7}{2^{3log_25}}=\frac{27\times 7}{5^3}=\frac{189}{125}\)
分析法1:利用二次函数求解;
转化为仿二次不等式\(ax^2-4x+a-3<0\)能成立,分类讨论如下:
①当\(a=0\)时,不等式为\(-4x-3<0\),故\(x>-\cfrac{3}{4}\),有解,故满足;
②当\(a>0\)时,二次不等式\(ax^2-4x+a-3<0\)能成立,必须\(\Delta >0\),解得\(0<a<4\);
③当\(a<0\)时,二次不等式\(ax^2-4x+a-3<0\)必然有解,故满足;
综上所述,\(a\in (-\infty,4)\)。
法2:分离参数法,\(a<\cfrac{4x+3}{x^2+1}\)在\(R\)上能成立,
令\(h(x)=\cfrac{4x+3}{x^2+1}\),用导数法求得\(h(x)_{min}=4\),此处略。
故\(a<4\),即\(a\in (-\infty,4)\)。
法1:一般式,设\(f(x)=ax^2+bx+c(a\neq 0)\),
由题意得\(\begin{cases}4a+2b+c=-1\\a-b+c=-1\\ \cfrac{4ac-b^2}{4a}=8\end{cases}\),解得\(\begin{cases}a=-4\\b=4\\c=7\end{cases}\),
故\(f(x)=-4x^2+4x+7\)。
法2:顶点式,设\(f(x)=a(x-m)^2+n\),由题意得\(n=8\),
又\(f(2)=f(-1)\),故函数的对称轴是\(x=\cfrac{2+(-1)}{2}=\cfrac{1}{2}\),故\(m=\cfrac{1}{2}\)。
则\(y=f(x)=a(x-\cfrac{1}{2})^2+8\),又\(f(2)=-1\),\(a(2-\cfrac{1}{2})^2+8=-1\),
解得\(a=-4\),故\(f(x)=-4x^2+4x+7\)。
法3:两根式(零点式),由已知\(f(x)+1=0\)的两根\(x_1=2\),\(x_2=-1\),
故可设\(f(x)+1=a(x+1)(x-2)\),
即\(f(x)=ax^2-ax-2a-1\),又函数\(f(x)_{max}=8\),即\(\cfrac{4a(-2a-1)-a^2}{4a}=8\),
解得\(a=-4\)或\(a=0(舍去)\),故\(f(x)=-4x^2+4x+7\)。
法1:(将\(b\)和\(\lambda\)看做系数)将不等式转化为\(a^2-\lambda ba+8b^2-\lambda b^2\ge 0\)对任意的\(a\in R\)恒成立,
则\(\Delta =b^2\lambda^2-4(8b^2-\lambda b^2)=b^2(\lambda^2+4\lambda-32)\leq 0\),
解得\(-8\leq \lambda \leq 4\)。
法2:变量集中策略,当\(b=0\)时,即\(a^2\ge 0\)恒成立,\(\lambda\in R\);
当\(b\neq 0\)时,原不等式等价于\((\cfrac{a}{b})^2+8\ge \lambda (\cfrac{a}{b})+\lambda\),
令\(\cfrac{a}{b}=t\in R\),即\(t^2-\lambda t+8-\lambda\ge 0\)对任意的\(t\in R\)恒成立,
则\(\Delta =(\lambda)^2-4(8-\lambda)\leq 0\),
解得\(-8\leq \lambda \leq 4\)。
综上所述(两种情况取交集),实数\(\lambda\)的取值范围为\(-8\leq \lambda \leq 4\)。
分析:若\(a=0\)时,原不等式等价于\(-x+1<0\),即\(x>1\);
若\(a<0\)时,原不等式等价于\((x-\cfrac{1}{a})(x-1)>0\),解得\(x<\cfrac{1}{a}\)或\(x>1\);
若\(a>0\)时,原不等式等价于\((x-\cfrac{1}{a})(x-1)<0\),
当\(\cfrac{1}{a}=1\)时,即\(a=1\)时,不等式无解;
当\(\cfrac{1}{a}<1\)时,即\(a>1\)时,不等式解集为\(\{x\mid \cfrac{1}{a}<x<1\}\);
当\(\cfrac{1}{a}>1\)时,即\(0<a<1\)时,不等式解集为\(\{x\mid 1<x< \cfrac{1}{a}\}\);
综上所述,
当\(a<0\)时,不等式解集为\(\{x\mid x<\cfrac{1}{a}\)或\(x>1\}\);
当\(a=0\)时,不等式解集为\(\{x\mid x>1\}\);
当\(0<a<1\)时,不等式解集为\(\{x\mid 1<x< \cfrac{1}{a}\}\);
当\(a=1\)时,不等式解集为\(\varnothing\);
当\(a>1\)时,不等式解集为\(\{x\mid \cfrac{1}{a}<x<1\}\);
实际高三数学教学和考试中的相关习题常常是这样的,理解掌握。
①\(x^2-5\sqrt{2}x+8\ge 0\),即\((x-\sqrt{2})(x-4\sqrt{2})\ge 0\);
②\(x^2-(2m+1)x+m^2+m-2\leq 0\),即\([x-(m+2)][x-(m-1)]\leq 0\);
③\(x^2-3mx+(m-1)(2m+1)\ge 0\);即\([x-(m-1)][x-(2m+1)]\ge 0\);
④\(x^2-(a+a^2)x+a^3\leq 0\),即\((x-a)(x-a^2)\leq 0\);
⑤\(x^2-(a+1)x+a\leq 0\),即\((x-1)(x-a)\leq 0\);
⑥\(x^2-(2a+1)x+a(a+1)\leq 0\);即\((x-a)[x-(a+1)]\leq 0\);
⑦\(\cfrac{x-2a}{x-(a^2+1)}<0(a\neq 1)\);即\((x-2a)[x-(a^2+1)]<0\),解集为\((2a,a^2+1)\);
⑧\(x^2+(m+4)x+m+3<0\),即\((x+1)[x+(m+3)]<0\);
分析:做出适合题意的图像,由图像可知,函数\(f(x)\)的值域为\([-1,1]\),
完整的偶函数\(g(x)\)的解析式应该为\(g(x)=log_2|x|\),若存在实数\(a\),使得\(f(a)=g(b)\),
则\(g(b)\)必须满足\(-1\leqslant g(b)\leqslant 1\),即\(-1\leqslant log_2|b|\leqslant 1\),
上式可以转化为\(\left\{\begin{array}{l}{b\geqslant 0}\\{-1\leqslant log_2b\leqslant 1}\end{array}\right.\)或者\(\left\{\begin{array}{l}{b<0}\\{-1\leqslant log_2(-b)\leqslant 1}\end{array}\right.\)
解得\(\cfrac{1}{2}\leqslant b\leqslant 2\)或\(-2\leqslant b\leqslant -\cfrac{1}{2}\). 故选\(B\).
法1分析:函数\(f(x)=lnx-x^3\)与\(g(x)=x^3-ax\)的图像上存在关于x轴的对称点,即当\(x=x_0\)时,\(f(x_0)=-g(x_0)\)。
所以方程\(f(x)=-g(x)\)有解, 所以\(lnx-x^3=-x^3+ax\)有解,
所以\(lnx=ax\)在\((0,+\infty)\)有解,即方程\(a=\cfrac{lnx}{x}\)在\((0,+\infty)\)有解,
令\(h(x)=\cfrac{lnx}{x}\),由导数知识可知,\(f(x)\)在\((0,e)\)上单调递增,在\((e,+\infty)\)上单调递减,
又\(f(e)=\cfrac{1}{e}\),故函数\(h(x)\in (-\infty,\cfrac{1}{e}]\),故\(a\)的取值范围为\((-\infty,-\cfrac{1}{e}]\) ,选D。
法2:转换为方程\(lnx=ax\)在\((0,+\infty)\)有解,即函数\(y=lnx\)和函数\(y=ax\)图像在\((0,+\infty)\)上有交点,利用数形结合求解;
法3:接上转换为方程\(a=\cfrac{lnx}{x}\)在\((0,+\infty)\)有解,即函数\(y=h(x)=\cfrac{lnx}{x}\)和函数\(y=a\)的图像有交点,利用数形结合求解;
法1:转化为方程\(a=x^2-2lnx+2\)在\(x\in [\cfrac{1}{e},e]\)内有两个根,
即函数\(y=a\)和函数\(y=g(x)=x^2-2lnx+2\)在\(x\in [\cfrac{1}{e},e]\)内有两个交点,
\(g'(x)=2x-\cfrac{2}{x}=\cfrac{2(x-1)(x+1)}{x}\),则在\([\cfrac{1}{e},1]\)上单调递减,在\([1,e]\)上单调递增,
又\(g(1)=3\),\(g(\cfrac{1}{e})=4+\cfrac{1}{e^2}\),\(g(e)=e^2>4+\cfrac{1}{e^2}\),
做出示意图,可知实数\(a\)的取值范围为\(a\in (3,4+\cfrac{1}{e^2}]\)
法2:由函数\(y=a+2lnx\)与函数\(y=x^2+2\)的图像在\(x\in [\cfrac{1}{e},e]\)内有两个交点,
则可知函数\(f(x)=2lnx-x^2+a-2\)在\(x\in [\cfrac{1}{e},e]\)内有两个零点,
\(f'(x)=\cfrac{2}{x}-2x=\cfrac{-2(x^2-1)}{x}=\cfrac{-2(x+1)(x-1)}{x}\)
则当\(x\in [\cfrac{1}{e},1]\)时,\(f'(x)>0\),\(f(x)\)单调递增,
当\(x\in [1,e]\)时,\(f'(x)<0\),\(f(x)\)单调递减,
又由于\(f(1)=2ln1-1+a-2=a-3\),\(f(\cfrac{1}{e})=2ln\cfrac{1}{e}-\cfrac{1}{e^2}+a-2=-4-\cfrac{1}{e^2}+a\),
\(f(e)=2lne-e^2+a-2=-e^2+a\),\(f(\cfrac{1}{e})>f(e)\),
则要使得函数\(f(x)=2lnx-x^2+a-2\)在\(x\in [\cfrac{1}{e},e]\)内有两个零点,
必须满足条件\(\left\{\begin{array}{l}{f(1)=a-3>0}\\{f(\cfrac{1}{e})=-\cfrac{1}{e^2}-4+a\leqslant 0}\end{array}\right.\)
解得\(3<a\leqslant \cfrac{1}{e^2}+4\),即可知实数\(a\)的取值范围为\(a\in (3,4+\cfrac{1}{e^2}]\)
标签:辅导 lock des document 文字 必须 cal inf 注意
原文地址:https://www.cnblogs.com/wanghai0666/p/12249262.html