标签:不用 有一个 ret write 处理 rom 最长路径 sed 中介
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ 2 3 <---
\ 5 4 <---如果按正确的顺序访问每个节点,就可以有效地获得二叉树的右视图。
上面提到的顺序之一可以由深度优先搜索定义。在深度优先搜索中,我们总是先访问右子树。这样就保证了当我们访问树的某个特定深度时,我们正在访问的节点总是该深度的最右侧节点。于是,可以存储在每个深度访问的第一个结点,一旦我们知道了树的层数,就可以得到最终的结果数组。
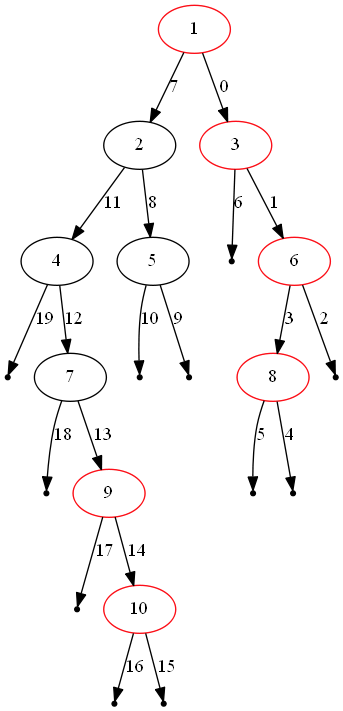
上图表示了问题的一个实例。红色结点自上而下组成答案,边缘以访问顺序标号。
class Solution(object):
def rightSideView(self, root):
rightmost_value_at_depth = dict() # depth -> node.val
max_depth = -1
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if node is not None:
# maintain knowledge of the number of levels in the tree.
max_depth = max(max_depth, depth)
# only insert into dict if depth is not already present.
rightmost_value_at_depth.setdefault(depth, node.val)
stack.append((node.left, depth+1))
stack.append((node.right, depth+1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth+1)]class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
/* These two stacks are always synchronized, providing an implicit
* association values with the same offset on each stack. */
Stack<TreeNode> nodeStack = new Stack<TreeNode>();
Stack<Integer> depthStack = new Stack<Integer>();
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
max_depth = Math.max(max_depth, depth);
/* The first node that we encounter at a particular depth contains
* the correct value. */
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth+1);
depthStack.push(depth+1);
}
}
/* Construct the solution based on the values that we end up with at the
* end. */
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}时间复杂度 : O(n)。一棵只有子指针的二叉树是一个只有一个源节点的有向无环图, 从根开始的遍历会经过每个结点一次,加上次线性数量的叶子 None。每次访问只需要 {O}(1)O(1) 的时间,故 while 循环只需要线性时间。最后,构造右视图的数组需要 {O}(O(height of the tree) = {O}(n))=O(n),因为右视图不可能包括比树本身更多的元素。
空间复杂度 : O(n)。最坏情况下,栈内会包含接近树高度的结点数量。由于采用深度优先,栈中永远不会有来自同一个父节点不同子树的两个结点。换而言之,一个结点的整个右子树将在左子树的任何节点被压栈之前访问。按此逻辑递归处理整棵树,当我们到达树的最长路径(树的高度)的末端时,栈将最大。然而,由于我们对树的结构一无所知,树的高度可能等于nn,导致空间复杂度为 {O}(n)O(n)。
就像深度优先搜索可以保证我们最先访问某个深度的最右结点那样,广度优先搜索可以保证我们 最后 访问它。
通过执行将左结点排在右结点之前的广度优先搜索,我们对每一层都从左到右访问。因此,通过只保留每个深度最后访问的结点,我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成 deque(双向队列),并去除了rightmost_value_at_depth之前的检查外,算法没有别的改动。
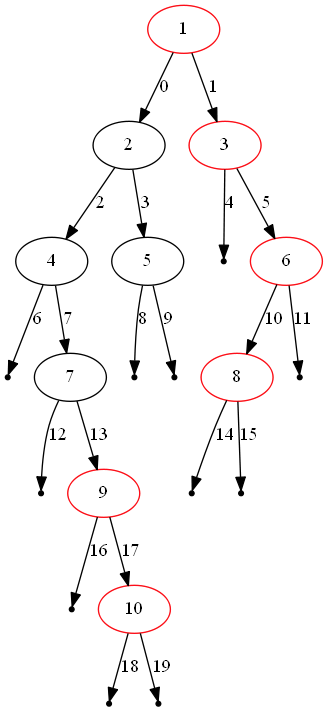
上图表示了同一个示例,只是方法改成了广度优先搜索。红色结点自上而下组成答案,边缘以访问顺序标号。
from collections import deque
class Solution(object):
def rightSideView(self, root):
rightmost_value_at_depth = dict() # depth -> node.val
max_depth = -1
queue = deque([(root, 0)])
while queue:
node, depth = queue.popleft()
if node is not None:
# maintain knowledge of the number of levels in the tree.
max_depth = max(max_depth, depth)
# overwrite rightmost value at current depth. the correct value
# will never be overwritten, as it is always visited last.
rightmost_value_at_depth[depth] = node.val
queue.append((node.left, depth+1))
queue.append((node.right, depth+1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth+1)]class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
/* These two Queues are always synchronized, providing an implicit
* association values with the same offset on each Queue. */
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<Integer> depthQueue = new LinkedList<Integer>();
nodeQueue.add(root);
depthQueue.add(0);
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.remove();
int depth = depthQueue.remove();
if (node != null) {
max_depth = Math.max(max_depth, depth);
/* The last node that we encounter at a particular depth contains
* the correct value, so the correct value is never overwritten. */
rightmostValueAtDepth.put(depth, node.val);
nodeQueue.add(node.left);
nodeQueue.add(node.right);
depthQueue.add(depth+1);
depthQueue.add(depth+1);
}
}
/* Construct the solution based on the values that we end up with at the
* end. */
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}时间复杂度 : O(n)。 算法 一节中介绍的改动不会改变时间复杂度。
空间复杂度 : O(n)。由于广度优先搜索逐层访问整棵树,在访问最大的层之前,队列将最大。该层最坏的情况下可能有 0.5n = {O}(n)0.5n=O(n) 大小(一棵完整的二叉树)。
deque
数据类型来自于
collections 模块,支持从头和尾部的常数时间a ppend/pop 操作。若使用 Python 的 list,通过 list.pop(0) 去除头部会消耗 O(n) 的时间。
递归方法是分别遍历一个节点的右节点和左节点,因为是从右边看过来,所以我们需要首先遍历右节点。这里有个疑问,当遍历左节点时候,怎么判定它右边没有其他节点了呢?这里我们用到一个变量level,对于同一层的节点,如果res数组的大小已经等于level了,说明右边已经有节点存入数组了,该节点就不用再保存。一直递归下去就可以得到结果。
代码一:
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
helper(root,0,res);
return res;
}
void helper(TreeNode* root,int level,vector<int>& res){
if(!root) return;
if(res.size()==level) res.push_back(root->val);
helper(root->right,level+1,res);
helper(root->left,level+1,res);
}
};这道题要求我们打印出二叉树每一行最右边的一个数字,实际上是求二叉树层序遍历的一种变形,我们只需要保存每一层最右边的数字即可,还是需要用到数据结构队列queue,遍历每层的节点时,把下一层的节点都存入到queue中,每当开始新一层节点的遍历之前,先把新一层最后一个节点值存到结果中,代码如下:
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
if(!root) return res;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
res.push_back(q.back()->val);
int size=q.size();
for(int i=0;i<size;++i){
TreeNode* t=q.front(); q.pop();
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
}
return res;
}
};标签:不用 有一个 ret write 处理 rom 最长路径 sed 中介
原文地址:https://www.cnblogs.com/wwj99/p/12251845.html