单调栈

标签：info   font   高度   media   整数   测试   12px   www   数据   

个人理解定义：栈中元素都是单调关系的栈数据结构。

模拟单调栈

7 2 1 4  

第一次为7 栈为空    7入栈   此时栈内 7

第二次为2  栈顶为7  7>2    2入栈  此时栈内   7  2

第三次为1  栈顶为2  2>1    1入栈  此时栈内   7  2   1

第四次为4  栈首为1  1<4    1出栈     继续往前比  栈首为2  2出栈  栈顶7  7>4  4入栈  此时栈内   7  4  

如果不是空栈入栈的数字一定会比前面所有数字小，如果一个数字大于栈内前面所有数字，则该数字入栈其余数字全部出栈。

单调栈伪代码

　　  for(遍历数组)

　　if(空栈或者当前数字比栈顶数字小或者一样)入栈

else 

{

　　while(不是空栈和找到比当前数字大的栈内元素)

{　　

当前栈顶出栈

 - -

}

　　　　当前数字入栈

}

实战环节

131. 直方图中最大的矩形

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

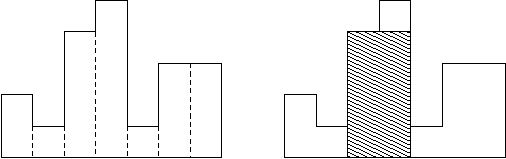
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hnh1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤1000001≤n≤100000,
0≤hi≤10000000000≤hi≤1000000000

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

纯模拟做法
7 2 1 4 5 1 3 3  确定 7 2  1  和 4 5 1  和 3 3 为三个可以组成的小矩形然后一个个求面积，其实就是遍历数组，然后寻找左右两边高于或者等于当前遍历到能组成的矩形的高度的边界也就是找到其中高最小的边界。然后一路更新矩形面积求最大。

单调栈做法

  建立一个空栈，首先入栈第一个数字确定了这个矩阵的高度，（如同例子7 2 1 4 5 1 3 3  使用肉眼观察法 可以发现可以组成7 2 1   ，4 5  1，3 3的三个区间，然后用思考法发现每个矩形区间如果确定了第一个高度的可以一直入比它小的数来确定一个区间直到当一个数大于栈顶的数 ）所以如果说我们入栈了一个数时此时栈为空或者大于栈顶时就已经确定了这个矩阵的高度的话,那么其实这个矩阵已经确定了它的左右边界，然后一路更新这个矩形区域的宽度，然后算出面积，然后因为题目求最大面积，然后一路更新。

核心代码：

        for(int i=1;i<=n+1;i++)//遍历数组
        {
            if(a[i]>s[p]) s[++p]=a[i],w[p]=1;// 当前数字大于栈首 它是一个独立的小矩形区间，w数组用来统计每个矩形区域的宽度，给他宽度赋值1
            else{
                int width=0;
                while(s[p]>a[i])           //找到该矩形区间的最高的位置为止
                {
                    width+=w[p];          //更新宽度
                    ans=max(ans,(long long)width*s[p]);//一路更新看是否是最大值
                    p--;　　　　　　　　　　　　//更新位置
                }
                s[++p]=a[i]；         //该矩形区间面积已经算完，仅需存留该矩形区间最小值和宽度
　　　　　　　　　w[p]=width+1;  　　//更新宽度
            }
        }

因为该核心代码中用了w数组来统计矩形区域的宽度

写下最后的数组即

最后最最重要的一步，定义数组a[n+1]=0

因为0肯定小于所有栈内的数字，所以能最后为所有矩形区间左右边界求面积并更新出最大值。 

单调栈

标签：info   font   高度   media   整数   测试   12px   www   数据   

原文地址：https://www.cnblogs.com/johnfllora/p/12253556.html