标签:MTA 图片 des 情况 ima inline 定义 需要 nali
Heaps and Heapsort:
堆是一种快速访问最大优先级元素的数据结构,这是快速实现选择排序的基础,但是总体来说平均速度比快排要慢一点,不过其最坏情况和平均情况是差不多的。
首先是堆的定义,每个结点比它的孩子结点都小(所以父节点最小),或者每个结点都比它的孩子结点大(父节点最大),把A[1,n]看做一个堆,i的两个孩子结点分别是2i和2i+1,这个非常方便实用。接着是删除堆的最小值(最大值同理),想法就是先删除最小值,然后把最后一个元素放到根节点并且不断sift-down,这个是一个结点下沉操作,即当前结点和两个子结点(如果有的话)中的最小者交换,继续下沉。然后是插入堆元素,想法是在最后的一个位置(i = n + 1)加入元素,然后sift-up,也就是和父节点比较,小的往上,大的下沉。同时无论是sift-down或者是sift-up都是O(logn)的。
于是我们可以提出堆排序的想法,也就是每次都删除最值,然后整理我们的堆,最后的总代价是O(nlogn)的,因为最差的代价t(n) <= t(2/3n) + t(1/3n) + O(logn),同时建堆的复杂度也是O(n)的,所以这个算法还是可以接受的。
Fibonacci Heaps:
在介绍斐波那契堆之前先来介绍二项树,高度为h的二项树由两棵高度为h-1的二项树得到,其中一棵二项树的根接到另外一棵二项树上面。h = 0的时候只有一个单一结点,由此可以递推得到其他的情况。用二项树来存结点的话需要用多棵二项树;举个例子,如果我们要存n个东西,那么我们先把n二进制表示,如果第i位是1(i >= 0),那么就构造一棵高度为i的二项树,这样一来就得到若干的二项树,结点数目之和为n。每棵树都是按照堆结构来存储,但是最小的那个元素并没有预先规定存在哪棵二项树里面,举个例子说:我们本来要存11个元素,再加入1个元素,那么就会得到下面的图:
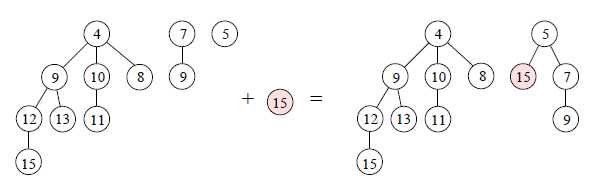
这里我们发现二项树的规模从8,2,1变成8,2,1,1变成8,2,2变成8,4。因为一种规模的二项树最多只有一棵!(结合二进制表示来理解)
讲完了二项树,我们来讲一下斐波那契堆,斐波那契堆是一些有序堆构成的树的集合,有一种想法是即为二项树的集合,但我们希望更加灵活一点,很重要的一点是知道斐波那契堆的结点是如何联系在一起的。这里面,兄弟结点用双向循环链表联系,而且每一个结点有一个指针指向自己的一个孩子节点,以及一个指针指向自己的父节点。除了指针,每一个结点有一个关键词,它的度数,以及一个逻辑位(标志marked/unmarked)。有序堆的根节点用双向循环链表连接,而且有一个特殊的指针指向最小的那个结点。
接下来介绍几个斐波那契堆的操作。给定两棵二项树,连接就是把root较大的那棵树放到root较小的那棵树下,作为它的孩子,也称为link操作;解体一个二项树或者是其子树,我们只要把对应的root从其所在的双向循环链表里面删除就可以了,也称为unlink操作;最后,要结合两个双向循环链表,我们切断所有的开端并在结尾连接,我们称为merge。图示如下:
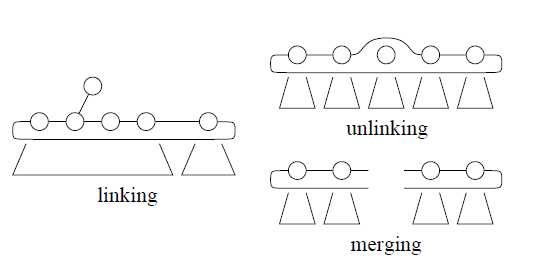
以上三个操作都是常数时间内的操作。
后来讲了用势函数来分析斐波那契堆的各种操作。首先是定义势函数,令ri为root cycle中的个数,mi为marked nodes的个数,势函数为ri + 2mi。第一个操作是getmin操作,由于不改变斐波那契堆的结构,所以ai = ci = 1;第二个是meld操作,也就是合并,也没有改变整体的数量,所以ai = ci = 1;第三个是insert插入操作,我们先创造一个斐波那契堆只有一个结点,然后把两个堆合在一起,root cycle中多了一个元素,所以势函数差值为1,ai = ci + 1 = 2。
接下来是delete min的操作,分下面四步。1)在root cycle中删除最小节点 2)把root cycle中的其他结点和删除结点的子结点merge 3)如果有root cycle中的结点的度数一样就不断合并 4)更改最小结点的指针位置,用势函数分析可以得到代价是O(logn)的;然后是decreasekey and delete,其中decreasekey是O(1)的,delete a node是O(logn)的。
总结一下见下图:

Solving Recurrence Relations:
说白了就是求解递推方程。文中用了一个比较奇葩的方法来求解,但是我觉得没什么必要,想法是用<a1,a2,....>来表示所有的项,规定一个操作L是把<a1,a2,a3,...>变成<a2,a3,...>,以及这样的形式可以构成线性空间(对加法和数乘满足八条性质),然后就去凑零化的形式。比如斐波那契数列的零化多项式是L^2 - L - 1,然后求解这个方程。比较有用的是介绍了一个主定理:
设T(n) = aT(n/b) + f(n)是关于复杂度T的一个递推关系,设c = n^(log(b)a),比较c和f(n)的大小,如果f(n)可以用n^(c-e)渐进逼近的话,那么T(n)就是n^c;如果f(n)和n^c同阶,就是n^clogn;如果f(n) >= Cn^(c+e),则为f(n)。比如归并排序中T(n) = 2T(n/2) + n,或者T(n) = 2T(n/2) + n^2等等。给三道题目吧:
1、T(N) = 2T(N/2)+NlogN,T(1)=1T(1)=1,则该算法的时间复杂度为?
2、T(N) = 2T(N/4) + sqrt(N), T(1) = 1, 求复杂度?
3、T(N) = T(N-1) + N, T(1) = 1,求复杂度?
Homework:

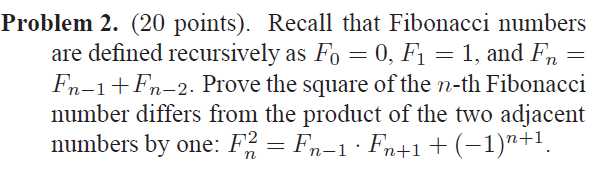



标签:MTA 图片 des 情况 ima inline 定义 需要 nali
原文地址:https://www.cnblogs.com/zyna/p/12251409.html