标签:style time graphic std review -128 不同的 examples section
Let‘s call two strings ss and tt anagrams of each other if it is possible to rearrange symbols in the string ss to get a string, equal to tt.
Let‘s consider two strings ss and tt which are anagrams of each other. We say that tt is a reducible anagram of ss if there exists an integer k≥2k≥2 and 2k2k non-empty strings s1,t1,s2,t2,…,sk,tks1,t1,s2,t2,…,sk,tk that satisfy the following conditions:
If such strings don‘t exist, then tt is said to be an irreducible anagram of ss. Note that these notions are only defined when ss and tt are anagrams of each other.
For example, consider the string s=s= "gamegame". Then the string t=t= "megamage" is a reducible anagram of ss, we may choose for example s1=s1= "game", s2=s2= "gam", s3=s3= "e" and t1=t1= "mega", t2=t2= "mag", t3=t3= "e":
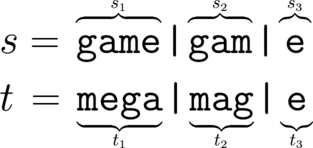
On the other hand, we can prove that t=t= "memegaga" is an irreducible anagram of ss.
You will be given a string ss and qq queries, represented by two integers 1≤l≤r≤|s|1≤l≤r≤|s| (where |s||s| is equal to the length of the string ss). For each query, you should find if the substring of ss formed by characters from the ll-th to the rr-th has at least one irreducible anagram.
The first line contains a string ss, consisting of lowercase English characters (1≤|s|≤2⋅1051≤|s|≤2⋅105).
The second line contains a single integer qq (1≤q≤1051≤q≤105) — the number of queries.
Each of the following qq lines contain two integers ll and rr (1≤l≤r≤|s|1≤l≤r≤|s|), representing a query for the substring of ss formed by characters from the ll-th to the rr-th.
For each query, print a single line containing "Yes" (without quotes) if the corresponding substring has at least one irreducible anagram, and a single line containing "No" (without quotes) otherwise.
aaaaa 3 1 1 2 4 5 5
Yes No Yes
aabbbbbbc 6 1 2 2 4 2 2 1 9 5 7 3 5
No Yes Yes Yes No No
In the first sample, in the first and third queries, the substring is "a", which has itself as an irreducible anagram since two or more non-empty strings cannot be put together to obtain "a". On the other hand, in the second query, the substring is "aaa", which has no irreducible anagrams: its only anagram is itself, and we may choose s1=s1= "a", s2=s2= "aa", t1=t1= "a", t2=t2= "aa" to show that it is a reducible anagram.
In the second query of the second sample, the substring is "abb", which has, for example, "bba" as an irreducible anagram.
/* 存在非反转组合的情况只有以下三种,看了半个小时英文解释也没弄清楚,就这样吧: 1.长度等于1 2.有至少3种不同的字母 3.首字母和尾字母不同 */ #include<iostream> #include<cstdio> #include<cstring> #define maxn 200010 using namespace std; int q,l,r,n; char s[maxn]; int sum[30][maxn]; int main(){ scanf("%s",s+1); n=strlen(s+1); for(int i=1;i<=n;i++){ int tmp=s[i]-‘a‘+1; for(int j=1;j<=26;j++)sum[j][i]=sum[j][i-1]; sum[tmp][i]++; } scanf("%d",&q); while(q--){ scanf("%d%d",&l,&r); if(l==r){ puts("Yes"); continue; } if(s[l]!=s[r]){ puts("Yes"); continue; } int cnt=0; for(int i=1;i<=26;i++){ if(sum[i][r]-sum[i][l-1]>0)cnt++; } if(cnt>=3){ puts("Yes"); continue; } puts("No"); } }
标签:style time graphic std review -128 不同的 examples section
原文地址:https://www.cnblogs.com/thmyl/p/12254744.html