标签:tps 等于 root stat 有一个 结构 ima sdn 判断
Q:输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
P.S.引用:https://blog.csdn.net/wuye999/article/details/100538399
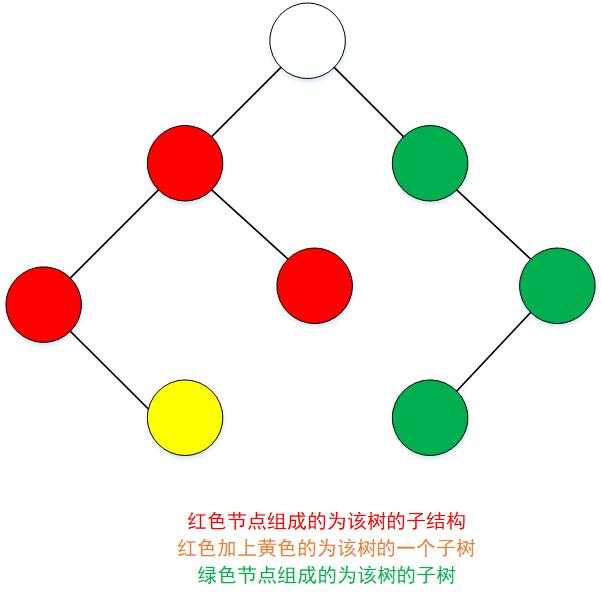
树的子结构:如果一个二叉树B是二叉树A的子结构,那么这要B这个结构在A中出现就可以。
树的子树:如果一个二叉树B是二叉树A的子树,那么二叉树B必是A的某个节点的左子树或者右子树或者就是二叉树A本身。
可以看出子树是要比子结构更加严格的,如果B是A的子树那必定是A的子结构,反之则不然。
下面有一个图说明二者的区别。
T:有三种情况,一种是根节点就是小树的根节点,那么去判断小树的子孙节点,如果都是满足,就是true,第二种和第三种就是小树在大树的左右子树中。
如果递归到大树都为空了,那么肯定是false,如果大树的根节点值不等于小树根节点值,那么说明这各节点不能做小树的根节点,返回false。如果递归到小树为空,说明此时小树的祖先节点都符合,那么就到了递归出口;如果左右子树都满足条件,那么也是true,那么就到了递归出口。
A:
static bool childlegal(TreeNode *pRoot1, TreeNode *pRoot2) {
if (!pRoot2)
return true;
if (!pRoot1)
return false;
return childlegal(pRoot1->left, pRoot2->left) && childlegal(pRoot1->right, pRoot2->right);
}
bool HasSubtree(TreeNode *pRoot1, TreeNode *pRoot2) {
if (!pRoot1 || !pRoot2)
return false;
return childlegal(pRoot1, pRoot2) || HasSubtree(pRoot1->left, pRoot2) ||
HasSubtree(pRoot1->right, pRoot2);
}P.S.一开始就考虑用先序中序确定唯一结构再确定子串,但……逻辑我没理顺。例如:
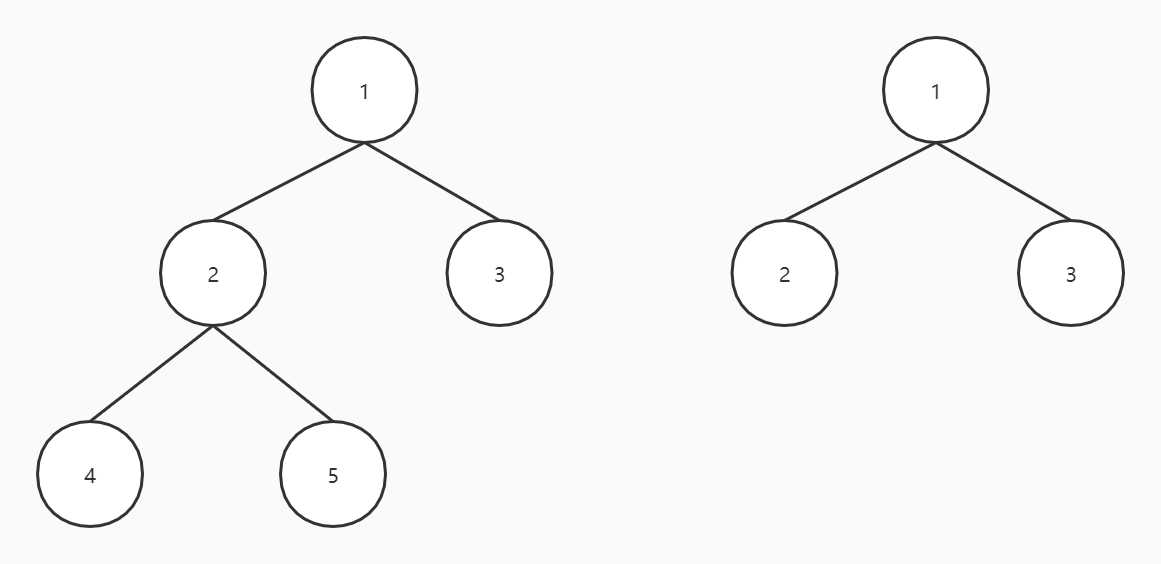
前面的先序为“12453”,后面的先序为“123”,前面的中序为“42513”,后面的中序为“213”,明显……不满足啊……遂,放弃。
标签:tps 等于 root stat 有一个 结构 ima sdn 判断
原文地址:https://www.cnblogs.com/xym4869/p/12256495.html