主席树总结

标签：int   dig   tps   names   define   git   模板题   bit   主席树   

主席树，即可持久化线段树，它是在权值线段树的基础上，记录了每个历史版本，从而可以方便快速的处理一些区间问题，最经典的应用有查询区间第 k 小。

当然，如果我们直接每次修改开一棵线段树，空间复杂度太大，肯定不行。但我们可以发现每次修改都只会改变一个结点的值，对于线段树来说，也就是只会有左儿子或者右儿子的值被改变，所以我们将没有改变的一半直接用之前的版本就好了。

用图片来解释主席树还是比较直观的。

橙色为历史结点。

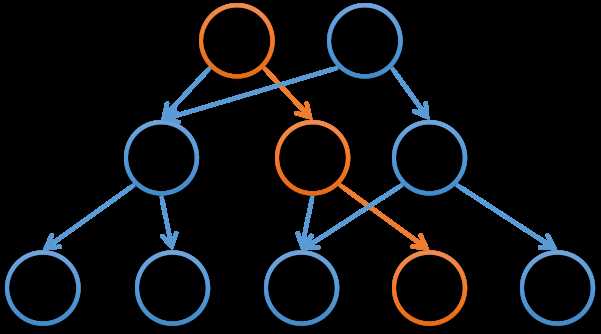
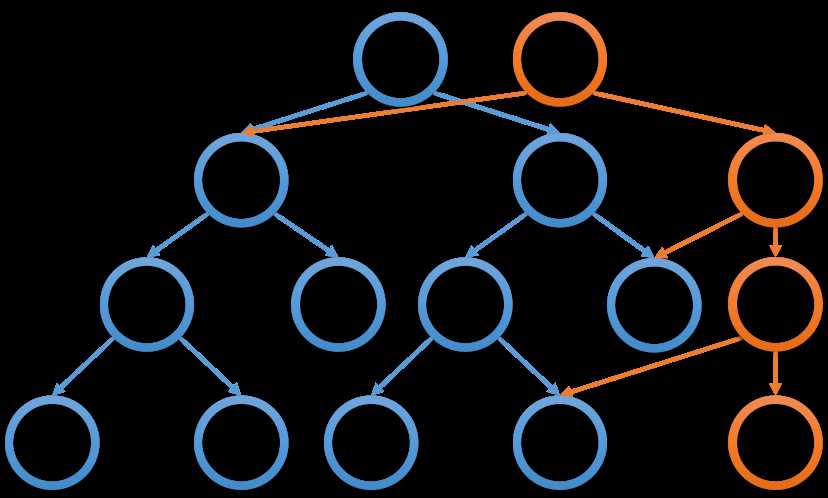
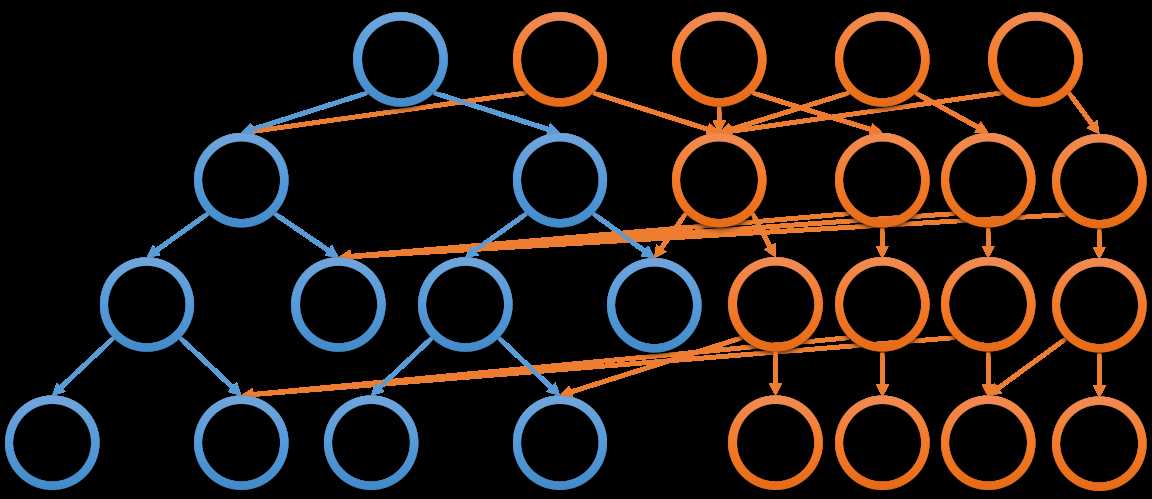
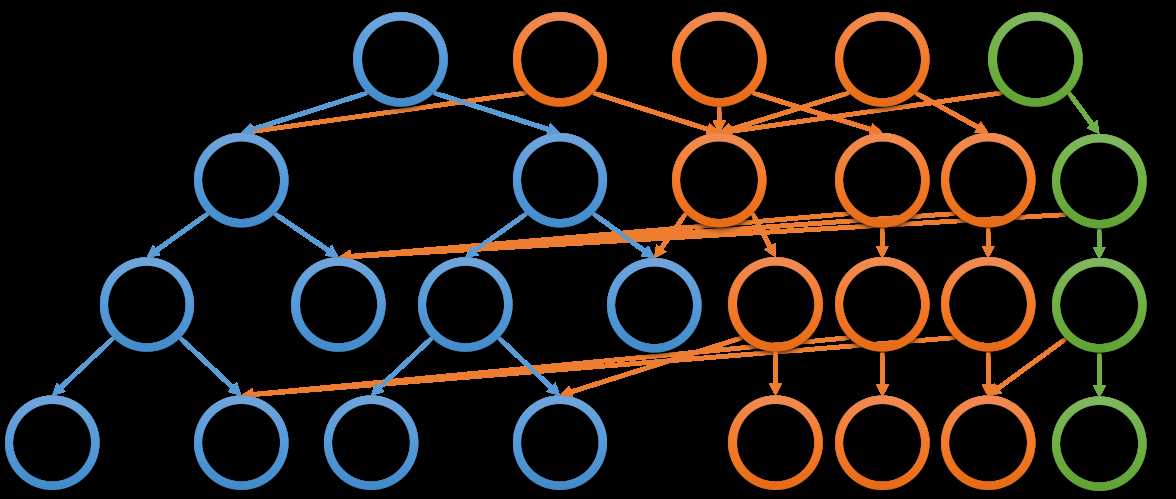
以上图片均出自 孤独·粲泽 大佬的 blog

代码

Luogu模板题

#include <bits/stdc++.h>
#define N 200005
using namespace std;

int gi() {
    int x = 0, f = 1; char c = getchar();
    for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
    for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    return x * f;
}

int n, m, tot;
int a[N], hs[N];
int cnt[N << 5], L[N << 5], R[N << 5], tr[N];

void modify(int lst, int &now, int l, int r, int k) {
    if (!now) now = ++tot;
    cnt[now] = cnt[lst] + 1;
    if (l == r) return;
    int mid = l + r >> 1;
    if (k <= mid) R[now] = R[lst], modify(L[lst], L[now], l, mid, k);
    else L[now] = L[lst], modify(R[lst], R[now], mid + 1, r, k);
}

int query(int u, int v, int l, int r, int k) {
    if (l == r) return l;
    int x = cnt[L[v]] - cnt[L[u]], mid = l + r >> 1;
    if (k <= x) return query(L[u], L[v], l, mid, k);
    else return query(R[u], R[v], mid + 1, r, k - x);
}

int main() {
    int l, r, k;
    n = gi(), m = gi();
    for (int i = 1; i <= n; ++i) a[i] = hs[i] = gi();
    sort(hs + 1, hs + 1 + n);
    int num = unique(hs + 1, hs + 1 + n) - hs - 1;
    for (int i = 1; i <= n; ++i) modify(tr[i - 1], tr[i], 1, num, lower_bound(hs + 1, hs + 1 + num, a[i]) - hs);
    for (int i = 1; i <= m; ++i) {
        l = gi(), r = gi(), k = gi();
        printf("%d\n", hs[query(tr[l - 1], tr[r], 1, num, k)]);
    }
    return 0;
}

主席树总结

标签：int   dig   tps   names   define   git   模板题   bit   主席树   

原文地址：https://www.cnblogs.com/hlw1/p/12257212.html