吴恩达深度学习课程第一课 — 神经网络与深度学习 — 第三周练习

标签：src   axis   矢量   深度   pre   偏差   image   img   会计   

第三周 - 浅层神经网络

第 21 题

以下哪项是正确的？（选出所有正确项）

A.\(a^{[2](12)}\)是第12层，第2个训练数据的激活向量

B.\(X\)是一个矩阵，其中每个列是一个训练数据

C.\(a^{[2]}_4\)是第2层，第4个训练数据的激活输出

D.\(a^{[2]}_4\)是第2层，第4个神经元的激活输出

E.\(a^{[2]}\)表示第2层的激活向量

F.\(a^{[2](12)}\)是第2层，第12个数据的激活向量

G.\(X\)是一个矩阵，其中每个行是一个训练数据

第 22 题

对于隐藏单元，tanh激活通常比sigmoid激活函数更有效，因为其输出的平均值接近于零，因此它可以更好地将数据集中到下一层。

A.对
B.不对

第 23 题

以下哪一个是\(l\)层的正向传播的正确矢量化实现，其中\(1 \le l \le L\)

A.
\(Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]}\)
\(A^{[l+1]}=g^{[l]}(Z^{[l]})\)

B.
\(Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]}\)
\(A^{[l+1]}=g^{[l+1]}(Z^{[l]})\)

C.
\(Z^{[l]}=W^{[l-1]}A^{[l]}+b^{[l]}\)
\(A^{[l]}=g^{[l]}(Z^{[l]})\)

D.
\(Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\)
\(A^{[l+1]}=g^{[l]}(Z^{[l]})\)

第 24 题

您正在构建一个用于识别黄瓜（y=1）与西瓜（y=0）的二进制分类器。对于输出层，您建议使用哪一个激活函数？

A.ReLU

B.Leaky ReLU

C.sigmoid

D.tanh

第 25 题

考虑以下代码：

A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)

B.shape是多少？

A.(4,)
B.(1, 3)
C.(, 3)
D.(4, 1)

第 26 题

假设你已经建立了一个神经网络。您决定将权重和偏差初始化为零。以下哪项陈述是正确的？（选出所有正确项）

A.第一隐藏层中的每个神经元将执行相同的计算。因此，即使在梯度下降的多次迭代之后，层中的每个神经元将执行与其他神经元相同的计算。

B.第一隐层中的每个神经元在第一次迭代中执行相同的计算。但是在梯度下降的一次迭代之后，他们将学会计算不同的东西，因为我们已经“破坏了对称性”。

C.第一个隐藏层中的每个神经元将执行相同的计算，但不同层中的神经元执行不同的计算，因此我们完成了课堂上所描述的“对称性破坏”。

D.即使在第一次迭代中，第一个隐藏层的神经元也会执行不同的计算，因此，它们的参数会以自己的方式不断演化。

第 27 题

逻辑回归的权重w应该随机初始化，而不是全部初始化为全部零，否则，逻辑回归将无法学习有用的决策边界，因为它将无法“打破对称”

A.对
B.不对

第 28 题

你已经为所有隐藏的单位建立了一个使用tanh激活的网络。使用np.random.randn(…, …)*1000将权重初始化为相对较大的值。会发生什么？

A.没关系。只要随机初始化权重，梯度下降不受权重大小的影响。

B.这将导致tanh的输入也非常大，从而导致梯度也变大。因此，你必须将\(\alpha\)设置得非常小，以防止发散；这将减慢学习速度。

C.这将导致tanh的输入也非常大，导致单元被“高度激活”。与权重从小值开始相比，加快了学习速度。

D.这将导致tanh的输入也非常大，从而导致梯度接近于零。因此，优化算法将变得缓慢。

第 29 题

考虑以下1个隐层的神经网络：

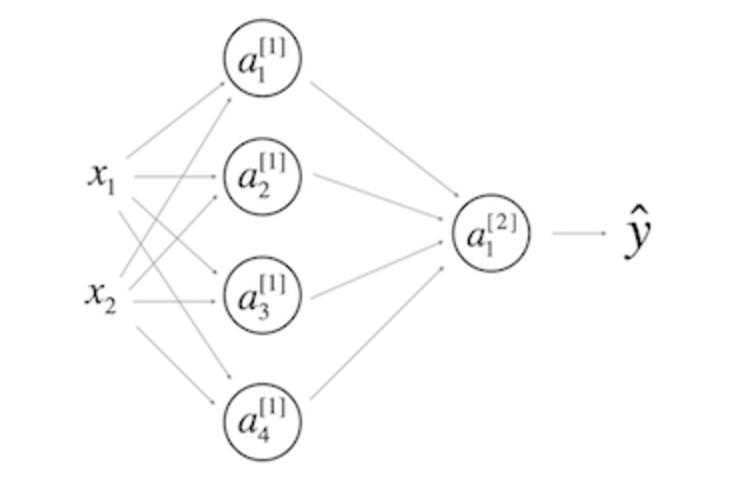
A.\(W^{[1]}\)的形状是(2, 4)

B.\(b^{[1]}\)的形状是(4, 1)

C.\(W^{[1]}\)的形状是(4, 2)

D.\(b^{[1]}\)的形状是(2, 1)

E.\(W^{[2]}\)的形状是(1, 4)

F.\(b^{[2]}\)的形状是(4, 1)

G.\(W^{[2]}\)的形状是(4, 1)

H.\(b^{[2]}\)的形状是(1, 1)

第 30 题

在和上一问相同的网络中，\(Z^{[1]}\) 和 \(A^{[1]}\)的维度是多少？

A.\(Z^{[1]}\) 和 \(A^{[1]}\)是(4, 1)
B.\(Z^{[1]}\) 和 \(A^{[1]}\)是(1, 4)
C.\(Z^{[1]}\) 和 \(A^{[1]}\)是(4, m)
D.\(Z^{[1]}\) 和 \(A^{[1]}\)是(4, 2)

21-30题 答案

21.BDEF 22.A 23.D 24.C 25.D 26.A 127.B 28.D 29.BC EH 30.C

吴恩达深度学习课程第一课 — 神经网络与深度学习 — 第三周练习

标签：src   axis   矢量   深度   pre   偏差   image   img   会计   

原文地址：https://www.cnblogs.com/YukiNote/p/12259149.html