标签:线性回归 png 理解 img span 就是 线性 样本 特征
之前我们讨论过一个线性回归的,里面是关于房屋售价和面积之间的关系,这个例子中特征只有一个,就是面积。
现在我们继续来讨论如果出现多个特征,通常情况下也是如此,人们在收售房屋时会考虑多个因素,比如新旧程度、地理位置、卧室数量、布局等等。这时特征数量不再是单一的,而是出现多个。
给出以下例子,考虑房屋面积、卧室数量、房屋年龄三个因素。
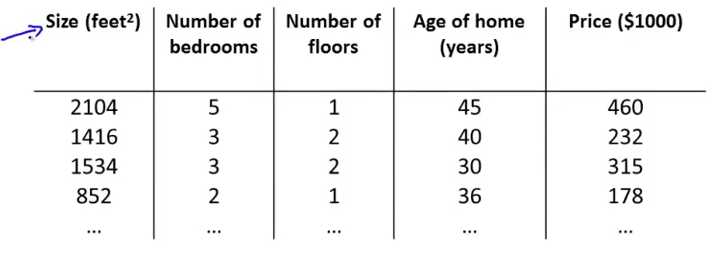
我们用 n 代表特征数量,m 代表样本数量,变量 x 此时也变为三个,即 x1 (代表面积),x2(代表卧室数量),x3(代表房屋年龄)。
定义 x(i) 代表第 i 个样本的所有特征值。例如 x(2) = [1416, 3, 2, 40, 232]
定义 xj(i) 代表第 i 个样本中第 j 个特征量。例如 x3(2) = 2
在这个例子中假设函数就为 h(θ) (x) = θ0 + θ1x1 + θ2x2 + θ3x3 ,我们令 x0 = 1, 可以得到 h(θ) (x) = θ0x0 + θ1x1 + θ2x2 + θ3x3
所以当特征有 n 个时, h(θ) (x) = ΘTX ,这就是多元线性回归的假设函数。
标签:线性回归 png 理解 img span 就是 线性 样本 特征
原文地址:https://www.cnblogs.com/feng-fengfeng/p/12261626.html