标签:算法 text mit 函数 logs 神经元 出现 alt 计算
虽然之前已经大概介绍了关于神经网络的基本结构,但是对于神经网络来说,还有很多可以提升的地方,包括不限于:参数的初始化,正则化,检测方式,除了梯度下降以外的优化算法,超参的调试,批量标准化,和TensorFlow等等。下面我们依次来介绍。
由于梯度消失/爆炸的原因,参数的初始化关系着神经网络模型性能的问题。常见的参数的初始化有以下几种:
所谓0初始化就是将所有的参数都初始化为零,但是由于初始化的值是一样的,它将不能破坏对称,以至于所有同源的参数的值将永远一样。
具有相同激活函数的两个隐藏单元连接到相同单元,那么这些单元必须具有不同的初始参数。一旦他们具有相同的初始参数,然后应用到确定性损失和模型的确定性学习算法将一直以相同的方式更新这两个单元。
为了破坏对称,我们可以用随机初始化参数。但是随机初始化同样会陷入梯度消失/爆炸的问题,使得学习速率很慢或使得模型准确率下降。
那么什么是梯度消失和梯度爆炸呢?

He初始化是在随机初始化的基础上,使得每一层的参数\(W^{[l]}\)经过缩放,使得\(A^{[l]}\)与\(X\)的均值类似,因此随机初始化的方差应为:\(\sqrt{\frac{2}{n^{l-1}}}\)
对于均值类似的原因从直观上来说:\(Z = w_1x_1 + ... + w_n x_n\)因此,当\(n\)越大的时候,\(Z\)的值越大,越容易出现梯度爆炸,因此直观上来说我们可以把\(w\)的方差\(var(w_i) = \frac{1}{n}\),事实上对于\(Relu\)激励函数来说我们常设为\(\frac{2}{n}\),\(n\)是前一层神经元的个数。
对于正则化我们主要解释两种正则化的方法:L2正则化和Dropout。那么,增加正则化项的目的是什么呢?在此之前,我们介绍一下过度拟合的问题:
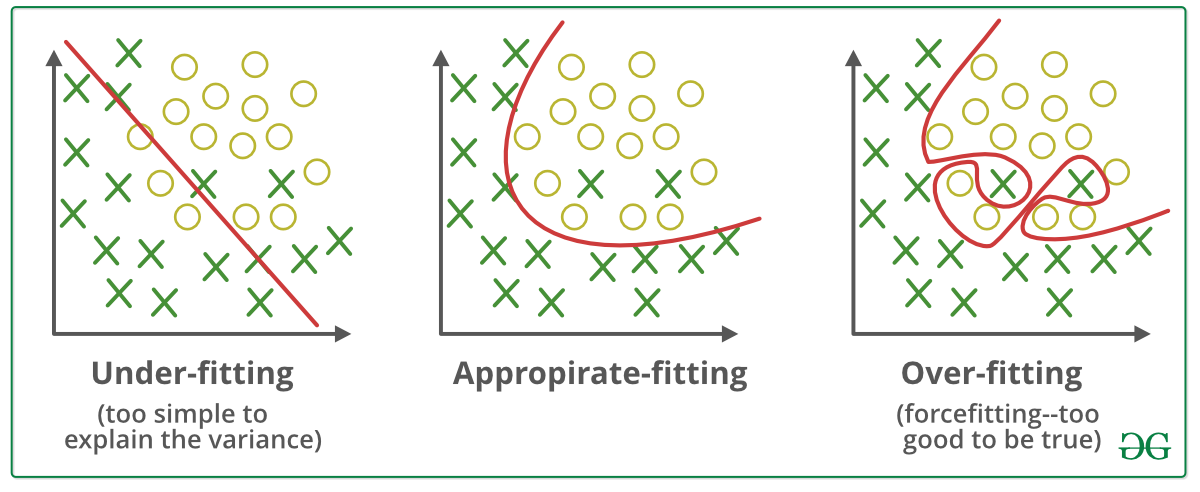
我们在Fig. 2 可以看到,拟合状态分为以下三种,分别是:欠拟合,正常拟合和过度拟合。
我们在神经网络的正向和反向传播中提及了Loss函数是:
Dropout是正则化的一种方式,由名字退出(drop out)可以看出,它是以随机除去神经元来使得减少某个神经元的依赖程度,达到可以使用正则化的方式。在应用过程中,我们设置一个新的变量\(D^{[l]} = \left[ d^{[l](1)}\, ... \,d^{[l](m)}\right]\)用以表示第\(l\)个隐藏层的\(D\),其中每一个\(d^{(i)}\)表示在第\(i\)个数据下的\(d\),而\(d\)表示的是该神经元是否隐藏。因此它将是一个由\(0\)和\(1\)组成的向量。使用\(d^{[l](i)} = np.random.rand(a^{[l](i)}.shape)<keep\_prob\)来设置\(d\)和\(D\)。之后为了使得输出结构的均值保持不变,在使用了Dropout的隐藏层在正向传播求得\(A^{[l]}\)之后还要再除以\(keep\_prob\)。并且在反向传播时也要将\(dA = \frac{dA}{keep\_prob}\)。
梯度检查是在检测Bug的过程中查看反向传播是否有错误的方法。使用公式:
\begin{equation}
\frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon}
\end{equation}
来进行梯度检查。
\begin{equation}
difference = \frac {\mid\mid grad - gradapprox \mid\mid_2}{\mid\mid grad \mid\mid_2 + \mid\mid gradapprox \mid\mid_2}
\end{equation}
\(gradapprox = \frac{J^+-J^-}{2\varepsilon}\)
当\(difference <10^{-7}\)时,我们说梯度计算是正确的。
标签:算法 text mit 函数 logs 神经元 出现 alt 计算
原文地址:https://www.cnblogs.com/x1ao/p/12261592.html