标签:内容 mamicode end 区分 大写 img class 函数 平面
以下内容没有找到任何参考资料,纯属个人想法。
如有错误,请多包含。
(这部分太过瞎搞所以另起一文
普通平面上的旋转矩阵如下:
\[
\begin{bmatrix}
cos\theta & -sin\theta\sin\theta & cos\theta\\end{bmatrix}
\]
而在复平面中,涉及到变换虚实数,三角函数会不太一样:
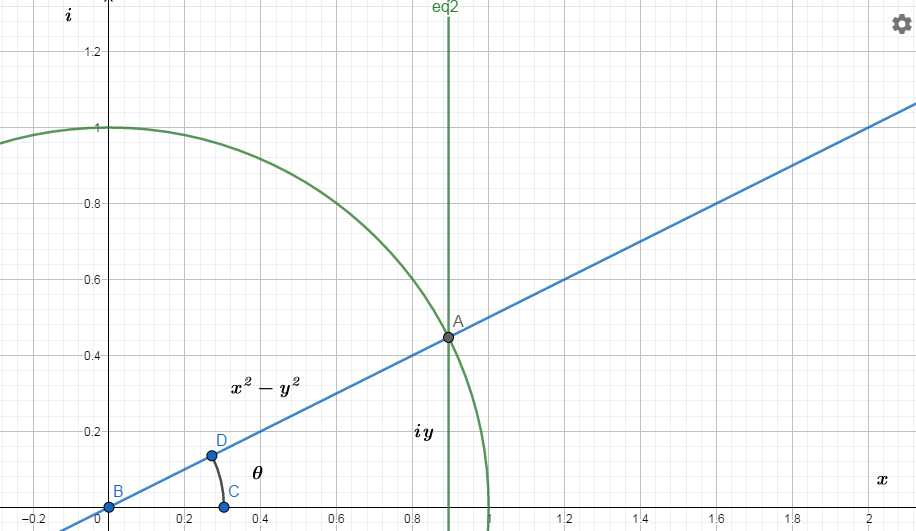
如图,复平面中,\(Cos\theta=\frac{x}{x^2-y^2}\;,\;Sin\theta=\frac{y}{x^2-y^2}i\;,\;Tan\theta=\frac{y}{x}i\) 。(为便于区分,复平面内三角函数首字母大写。)
那么复平面的旋转矩阵就是:
\[
\begin{bmatrix}
Cos\theta & -Sin\theta\Sin\theta & Cos\theta\\end{bmatrix}
\]
写成普通三角函数形式是:
\[
\begin{bmatrix}
cos\theta & -sin\theta i\sin\theta i & cos\theta\\end{bmatrix}
\]
大概差别就是复平面中的 \(sin\) 和 \(tan\) 是虚数。
(那我写这么多干什么
标签:内容 mamicode end 区分 大写 img class 函数 平面
原文地址:https://www.cnblogs.com/thornblog/p/12266186.html