标签:获得 标准 眼镜 领域 sigma 关系 视觉 ror 重要
卷积神经网络(CNN)作为深度学习的重要一支,在当前计算机视觉领域应用相当广泛。本文回顾了深度学习的发展历程,讲述CNN基本的理论概念和第一代卷积神经网络LeNet-5的建立。文章言有不当之处,还望批评指出,共同进步!

2015年,AlphaGo战败樊麾二段,"深度学习"的命运就此改变,这个曾被抛弃忘却的领域成为了数年至今无数人追求的研究方向。然而,它璀璨夺目的前世却充满了暗淡与不幸。
“深度学习”的概念正式提出是在2006年,狭义上可以看作是人工神经网络。最早的相关研究是19世纪40~60年代的控制论,已经提出了前馈层次网络摸型,也就是感知器,不过只是一种简单的线性模型。该模型功能类似于拟合$f(x,\omega )=x_0\omega_0+x_1\omega_1+...+x_n\omega_n$这样的函数,但在许多像异或问题的情形下显得无能为力。
直到80年代,Hinton等人提出了反向传播(BP)算法,使得模型具备了非线性映射的能力,解决了历史遗留下来的异或问题。但当时很多神经网络的研究者都是物理学家或者是心理学家,神经网络普遍不能被工程师和计算机科学家所接受。并且,因为受限于当时的数据规模,模型训练很容易出现“过拟合”,加上机器计算能力的不足和神经网络算法的“神秘性”,那些本就寥寥无几的研究者也逐渐对它失去了兴趣,纷纷转行钻研支持向量机(SVM)的机器学习算法。虽然如此,当时却仍有一些“固执”的探索者凭着坚定的信念在神经网络领域默默耕耘,其中就包括后来建立LeNet网络的Yann LeCun。
1998年,Yann LeCun等人在IEEE上发表了《Gradient-based learning applied to document recognization》一文,文中提出了基于梯度学习的卷积神经网络算法,并成功运用于手写数字识别中,取得了低于1%的错误率,超过了当时所有的模型,由此神经网络的研究开始回热。

第一个卷积神经网络并非是LeNet,而是1987年由Alexander Waibel等人提出的时间延迟网络(Time Delay Neural Network, TDNN)。TDNN是一个应用于语音识别问题的一维卷积神经网络,而二维网络则是由Yann LeCun提出的,并且论文中首次使用了“卷积”一词,所以以“第一人”称呼Yann LeCun不为过。
据吴恩达对LeCun的采访了解,LeCun从小就对科技兴致盎然,尤其是对“人类的智慧”、“有智慧的机器”等话题非常痴迷,最喜欢看有“现代科幻电影技术里程碑”美誉之称的《2001太空漫游》——看来幼时的兴趣着实能影响一个人的一生啊!后来在大学期间,LeCun通过一本辩论语言是否天生的哲学书间接了解到了“感知器”的概念。抱着满脑的好奇,他去了好几个大学的图书馆,想要找到有关的资料进一步学习,才发现在50年代之后就很少有人谈及到感知器了。
当LeCun拿到工程学位以后,LeCun去学习了与神经网络并不相关的芯片设计,但同时对研究神经网络仍念念不忘——在当时,还没有出现所谓的反向传播算法,如何训练多层网络依旧是困扰研究者的一大难题,LeCun因此特别想从事这方面的研究。幸运的是,老天从来不会辜负有理想并为之努力的人,LeCun在后来渐渐接触到了一些神经网络方面的研究者,这些人都多多少少对他产生过影响。例如,当时有群法国实验室的人正在研究自动机网络,给他看了一些前沿的论文,其中就有Hinton和Terrence写的关于玻尔兹曼机的文章,LeCun看后非常震惊,原来世界上有这样一群人已经找到了神经网络正确的研究方向。
后来在读博期间,LeCun有幸遇到了当年论文的作者之一Terrence,通过交流,他从Terrence那了解到了反向传播,这个概念当时还处于研究阶段,没有论文的发表。Terrence从法国回到美国后,就跟好友Hinton谈及了LeCun,几个月后Hinton的演讲会上,LeCun便认识了这位对他影响深远的导师。
LeCun最早开始研究卷积网络是在多伦多大学跟着Hinton做博士后的阶段。那时候没有像现在这样丰富完善的数据库,自然也没有现在被人“嚼烂”了的MNIST数据集,LeCun就用鼠标在个人电脑上一个一个地画出字符用作训练样本,就这样做出了早期的卷积神经网络,并且那时已经有超越传统网络的迹象了。再后来,不得不提的就是贝尔实验室了,可以说它是LeCun成功的重要平台。在实验室,LeCun拥有了自己专用的Sun4电脑(在多伦多大学一台Sun4电脑是整个学院共享的),当时实验室的主管Larry说,在贝尔实验室没有谁是能靠省钱省出名的。在刚加入实验室的三个月内,LeCun便用实验室原本建立的数据集USPS训练出了第一代LeNet,得到了实验室内最好的效果。虽然现在回过头看LeNet的架构已经相当普通了,甚至一些教程里都只是一笔带过,网上也有各种版本的复现,但对于当时环境来讲,没有Python、Matlab,没有Pytorch、TensorFlow等现成框架,网络的构建需要自己写模拟器和解释器,是相当复杂的。
再后来,被人所铭记的就是LeCun在98年的LeNet论文,论文中提及了LeNet5和自动机,标志着真正的CNN诞生了。现今任何的卷积网络你都可以看到LeNet的影子,Yann LeCun也同Geoffrey Hinton 和 Yoshua Bengio一起获得了2018年的图灵奖,并称为“深度学习三巨头”。
成功背后——在被问及深度学习的冬天时,LeCun说道,我一直坚信这些方法总有一天会回到大家的视野中,大家会学会如何用它们,解决一些实际问题。我一直有这个信念。
我个人刚接触深度学习并没有太长时间,同许多人一样,也是看着吴恩达老师的视频“长大”的。庆幸的是,我们学校有自组织的深度学习小组,所以在一定程度上讲,我并非是完全的自学,这一点我认为还是很重要的——众人的智慧总是比个人来得强大。同样,LeNet5也并非纯粹的个人成果,其中也汲取了时代的经验。此外,我认为,有些人学深度学习都是没有“根”的(有点狂妄了),这里所讲的“根”便是历史的概念。高中时候学历史总感觉兴味索然,认为历史无用,理科才是有“料”的;但反观物理学,了解物理的发展史是基本的素养。深度学习也是一样,当视频中讲到拟合、误差函数、梯度下降等概念的时候,总以为学到了一些很先进的概念,其实回顾历史,这些东西早在上世纪中期就差不多有了。
这一节主要讲的是在LeNet5提出前当时已有一些重要成果,也只是蜻蜓点水一般地描述,不会过度深入地解释,一来是自己的底子薄弱,二来也并非是文章的主旨。
神经网络的训练实质上就是网络权重的更新调整。现在的网络基本都采用计算损失函数结合梯度下降来更新参数,有趣的是,最早具备这种特征的算法在70年前差不多就存在了,该算法被称为Delta学习规则,其修正公式是$\omega_{ij}(t+1)=\omega_{ij}(t)+\alpha(d_i-y_i)x_j(t) $。其中,$\alpha$为学习速率,$d_i$和$y_i$为神经元i的期望输出和实际输出,$x_j(t)$为神经元j的状态(神经元i输入),可以发现,这跟我们现在的权重更新是很相似了,只是Delta学习规则是针对单层网络而言的,对于多层网络的权重更新,当时的人还是一头雾水。
不过从那时起到现在,人们对于如何从数据中学习的基本思想是一致的——无论什么样的网络,我们都希望,实际的输出和期望的结果间的差别最小(损失函数的内涵所在),而影响损失函数的便是网络的权重,所以可借助损失函数的梯度,来衡量参数对损失函数值的影响力大小,进而更新权重(梯度更新的内涵)。
在LeNet5论文中,作者曾谈到一个经验公式:

$E_{test}$和$E_{train}$分别表示测试集和训练集的误差;$k$和$\alpha$都是常数,$h$是网络复杂度水平,$P$表示数据集的大小。这个简单公式实际上可以当做是整个深度学习研究的潜在定律:首先,对深度学习有过了解的人都知道随着网络复杂度的增加,对训练集的拟合效果会越来越好,也就是训练集误差会下降,公式也验证了这个常识。那么这种情况下的测试集误差呢,一开始可能也是下降的,但下降的速度一般都比训练集慢,这就牵扯到网络的泛化能力了,假如复杂度再增加,如果数据集大小不变的话,很可能就会有过拟合问题冒出来。再来看数据集大小的影响,随着$P$的增大,测试集误差会无限接近训练集的误差,这往往是研究者们期望看到的结果。
在实际训练时,我们既想要训练集误差的下降,又想要测试集误差尽可能接近训练集误差,这就对硬件的性能和数据获取提出了巨大的挑战。即使在今日,我们也没办法将这两项都做到极致,力所能及的只是做到两者的平衡罢了,这也是当时研究者所能看到的状况。
神经网络发展过程出现了很多的梯度下降法,其中有很多好的算法可以加快下降、更容易找到全局最小值,比如现在普遍使用的Adam。但在90年代用的比较多的还是随机梯度下降SGD,SGD从60年代开始便有在研究了,只是到了80年代中期才被应用到网络上。总的来说,SGD每次采用个别样本来更新权重,这使得计算量减少了很多,收敛得也更快,不容易困在局部最小值里出不来,当然前提是训练集得足够大,稀释噪声带来的影响。
LeNet的出现或者CNN的发展都要感谢反向传播算法的提出。在反向传播算法提出以前,梯度下降都只能应用于线性网络中,因为人们无法很方便地求解多层网络间对参数的导数。反向传播实质上是链式法则的应用,相信一些像我一样的深度学习的初学者对反向传播的过程也不是很熟悉——现在的框架像TensorFlow具备了自动求导的功能,根本不需要手动一层层地向前求导了。之前知乎上看到胡渊鸣大神一篇文章讲述了自己曾被链式求导法则折磨了很久,于是最后将其开发的模拟器命名为ChainQueen来纪念那段经历,可知链式求导可不是说说那么简单的呀!
其实还有很多的技术可以一一说来的,但是精力和能力有限,这里不再叙述了。有兴趣的可以看看LeNet5论文,包含了很多当时的研究状况。
我们经常讨论一些很有意思的为什么,比如:“为什么自然选择人成为高等生物”、“为什么民主和法治是制度发展的趋势”、“为什么华为能成为行业的领先者”等等,这些问题似乎都遵循了物竞天择的道理。在卷积网络出现前,普遍使用的都是全连接的形式,卷积凭借什么特性能够独树一帜呢?本节将讲述卷积网络的基本概念和优越之处。
针对2D图像识别的全连接网络,首要的问题便在于参数过多。试想一下,一张32*32像素大小的手写字符图片作为第一层输入,假使第二层神经元数量只有100个,那么需要训练的数量就已经达到32*32*100=102400个了,何况一般的网络层数都要在3层以上。对于全连接网络,网络的连接数等于要训练的参数个数(不考虑偏置的话),一方面网络复杂性的提高是必须的,但是参数增加的同时所需要的训练数据也必须增加,否则就容易过拟合,因此全连接层带来的参数增长和过拟合问题在当时是著名的难题。
其次就是网络不具备特征不变性。最简单的例子就是,如果你拿一批字符都在中间的数据去训练的话,即使测试时准确率有多高,如果用一批字符都偏左边的数据去测试,那么得到的结果将大跌眼镜。其中原因就在于全连接层是顺序输入的,非常依赖于特征的位置信息,因此导致了它对平移、形变、扭曲等几何变换非常敏感。
进一步地说,因为全连接层是每个像素单独对应一个权重,而图像特征大多都是相邻像素的组合,这种做法显然忽视了图片像素的拓扑结构,就像是“管中窥豹”一般。再打个有趣的比方,我让你去识别一个数字,但规定了你一次只能看图片里的一个像素,这显然是故意为难你啊!
要了解卷积网络,就必须先了解什么是感受野。这个概念最早是在1959年的对猫的初级视皮层的一项研究中提出的,卷积网络便是受到了它的启发。
我们可以通俗地将感受野理解为眼睛所能看到的区域,比如说,眼睛可以看到整个图片的内容,那感受野就是一张图片那么大;如果也让这只眼睛来次“管中窥豹”,那感受野就可能减少为几个像素的大小了。例子的后者就可以认为是局部感受野,因为只能看见图片的一部分。现在,我们将网络的每一个神经元都看作一双双眼睛,那么情景就如下图一样,每双眼睛观察的地方都不一样,但视野大小相同,最终整个图片都会被窥看一尽。
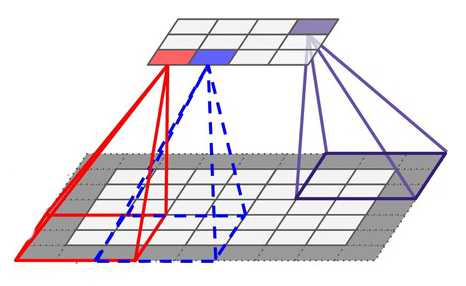
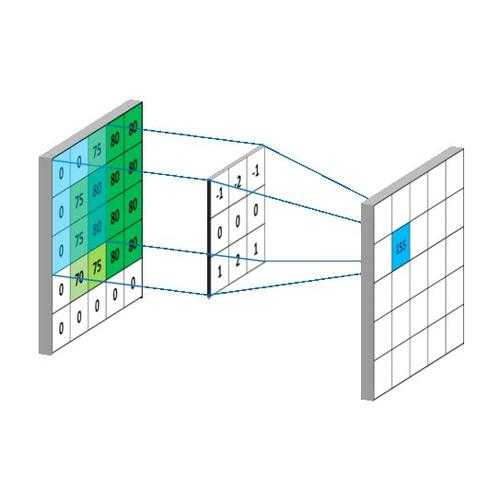
看的过程并非是漫无目地赏景,而是对视野内的像素作加权运算,感受野每个位置都有权重值,这些权重值就是网络的训练参数。加权所得的值作为这只“眼睛”的值,然后感受野会平移一定像素距离,这个距离称为步长。移动后的感受野再次加权运算,结果作为另一只“眼睛”的值。这样,前一层的图就会映射成新的图,这个图叫做特征图。
这就是局部感受野,相比于全连接,它同时考虑某个局部区域,这样更容易提取到想要的特征。
为什么叫做“特征图”呢?如果有接触过图像处理的话,会知道卷积在图像平滑、边缘等方面应用很多。一种权重的感受野(以下简称“一种感受野”)可能会“感受”到边缘特征,另一种感受野可能会“感受”到拐角特征。对于一张特征图来说,因为都是由同一种感受野观察到的,因此很可能就是一张某种特征的集合,只是这些特征分布在前一层图的不同位置。
我们将之前的模型推广一下,如下图所示,前一层图具有3个通道。在卷积的过程中,感受野不再是二维,而变成了三维形式,包含的权重参数也就有3*3*3=27个。感受野每平移一次,27个像素值线性加权,结果作为这只“眼睛”的值,卷积完毕后得到一个新特征图。在实际应用中,通常对前一层图卷积多次,每次使用不同的感受野,以获得多种特征。比如卷积4次,那么总共就用了4种三维感受野,得到4种特征。
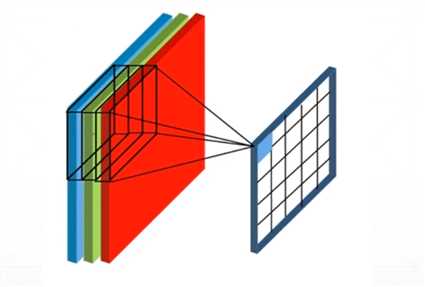
共享权重就体现在每次卷积只使用一种感受野。之所以将感受野变成三维模式,可以这么理解:在多层卷积网络中,某层网络有n通道的特征图,也就有n种特征;对该层卷积就是对这n个特征进行组合,获取更高维特征的过程,因而三维感受野的线性加权相当于特征的组合,权重不同,组合方式也不同。
再来算一下所产生的参数量,假设卷积4次,步长为1,感受野大小为3*3,前一层图大小为32*32,有3个通道。将感受野扩展为三维形式,一个感受野有3*3*3+3=30个参数(加上每个感受野有个偏置参数),于是总参数量为30*4=120个。经过卷积后生成的特征图大小为30*30(感受野不能超过图的边界,因此少了两行两列),共4个通道,那就有4*30*30个“眼睛”,每个眼睛在卷积时都有27+1根连接线,所以总连接数为4*30*30*28=100800。可以看到,在保持网络复杂性的同时,有效降低了需要训练的参数,这就是共享权重带来的好处。
向后层网络传递时,特征图的大小总是不断缩减,而通道不断增加的。这样做使得特征越来越多,越来越重要,而位置信息越来越少。事实上,物体的识别何尝不是这样的呢?例如,我们判断一个动物是不是猫,根本就不用在意它体型多大,是肥的还是瘦的;不用在意它坐在桌上,还是躺在床上。而是去看它的胡须、耳朵、鼻子等等的细节特征。再比如判断一个数字是不是7,我们会看它的三个端点的相对关系,至于它多少大、写得多少歪那只不过是审美上的事罢了。卷积网络更是这样,在最后几层的特征图里,你根本看不出是个啥玩意儿,因为太高维了!
卷积网络的这个特性在一定程度上要归功于下采样操作,它类似于卷积,不过不含权重,一般对每个通道都在感受野内选择最大值或者均值作为结果,因此下采样后特征图的大小会减小,但通道数仍不变。这种操作类似于将一张图片进行缩小,在缩小时主动丢失了一些像素信息,但是整体上看内容基本上没有发生变化。
很多教程上说,下采样有三种功效:一定程度的特征不变性、防止过拟合和减少参数量。最后一个功能是显而易见的,过拟合在参数减少情况下也相对难以出现,但是关于特征不变性我还不能很好理解(大佬如果知道,可以教教我),只能这样解释:下采样建立了一种激励机制,越有帮助的特征其值便越大,这通过网络的反馈和权重的调整应该是可以做到的,既而特征所处的位置就不再敏感,形变的输入也会因为这种机制凸显出所要的特征。
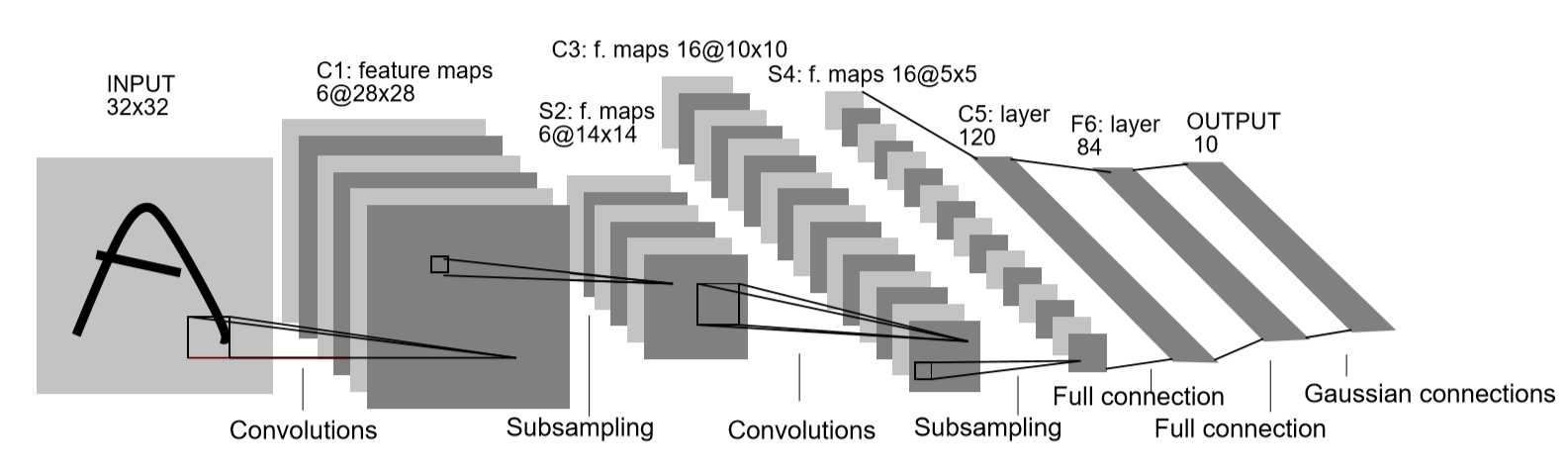
LeNet-5是为手写字符的识别专门而生的,LeCun后来也建立了MNIST数据库供人们使用,现在初学者一般都会拿这个数据集下刀。跑这个数据集的话,我还是很想建议用全连接层和LeNet-5跑一下的——用过笨办法,你才知道智慧是怎么来的。
LeNet-5当时用的图片大小是32*32的,这个跟现在的不一样,现在直接就是28*28了。其实32*32也是LeCun他们自己从28*28扩出来的,而现在的边缘处理由框架直接可以实现了。LeNet采用的是最原始的卷积下采样交替,全连接输出的结构。
输入的图像像素值都经过了严格的归一化处理,最后255对应了-0.1,0对应了1.175,归一化的过程作者并未提及,只是说这样处理后数据的均值近似0,方差近似为1,这与现在的概念差不了多少。
C1层、S2层很普通就不啰嗦了。C3层采用了很怪异的局部连接,就是每次卷积并非都对全部通道进行,而是有选择的进行,具体配置请看下图,至于这样有选择的进行特征组合是否有意义呢?很不好说,至少现在的网络都不这么做了。不过,这里有个很有趣的点——假如让LeCun在中间再加一层卷积,他还会不会这么干?表示很好奇。
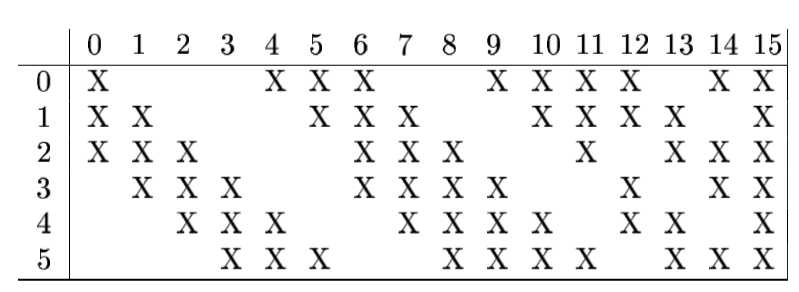
S4也略过。因为输入大小的巧合,所以C5层已经是被展平了,但是在结构上仍表示一层卷积,因此作者没有把它标成F5。图中的高斯连接涉及到了当时的RBF算法,类似于现在的softmax,这里也不深入探究了。
另外,除了输出层以外的层都采用了tanh型激活函数,在当时,sigma函数的缺点就已经被发现了。还有一个不同点就是,LeNet的下采样层也是有训练参数的,当时他采用的还是平均值采样,再乘以一个权重值。
最近正在学习卷积神经网络,打算好好琢磨一下这几年出现的经典网络。深度学习是一个很“玄学”的研究,有很多地方都值得去思考深究。之前看到有人问一个只专于图像处理算法研究的博主,为什么不去搞深度学习,博主评论道,如果你不去原理上研究深度学习,那这就是个调参的东西,没什么意思。
我前两天纠结要不要好好看一下LeNet论文,要不要写这样一篇回顾性的文章,毕竟LeNet对于现在来讲已经不怎么用了。就像前文提到的,你是倾向于紧追潮流,还是愿意先回头瞥一眼历史,这个话题在飞速发展的今天显得挺有意思。后来整理过程中,我觉得历史还是很重要的,历史能帮助我搞清楚自己研究这个的目的,是为了有一技之长,还是为了什么?
这里分享LeCun的一段话:
AI 这个领域和我刚刚进入的时候已经完全不一样了。我觉得这个领域现在有一点很棒,就是想要在一定程度上参与进来是很简单的一件事。我们现在有很多简单好用的工具,TensorFlow、PyTorch 等等一大堆,自己家里随便一个什么电脑就能运行得起来,然后训练一个卷积网络或者循环神经网络做任何想做的事情。除了这些工具,也还有很多线上的教学资源可以学习,没有什么门槛,高中生都能玩得转,我觉得这棒极了。而且现在的学生里对机器学习、AI 感兴趣的也越来越多,年轻人也能喜欢真的很好。
我的建议是,如果你想要进入这个领域的话,做出一些帮助,比如在开源项目里贡献一些代码,或者实现某个网上找不到代码的标准算法,这样别人就有得用了。你可以就找一篇你觉得重要的论文,把算法实现出来,然后做成开源的代码包,或者贡献到别的开源代码包里。如果你写的东西有趣、有用,就会有别人注意到你,你非常想去的公司可能会发 offer 给你,你很想读博的地方也可能给你回信,之类的。我觉得这是一种很好的开头方式。
最后,还是得感谢大家的阅读!
标签:获得 标准 眼镜 领域 sigma 关系 视觉 ror 重要
原文地址:https://www.cnblogs.com/kensporger/p/12267319.html