二叉堆

标签：bre   最大   图片   二叉树   12px   turn   bsp   操作   --   

什么是二叉堆

二叉堆本质是完全二叉树一种。分为最大堆和最小堆两种。

字面理解最大堆任何一个父节点的值都大于等于它左右孩子的值，最小堆则与之相反。

二叉堆的根节点叫做堆顶。最大堆的堆顶就是整个堆最大的数，最小堆则与之相反。

举个例子：最大堆

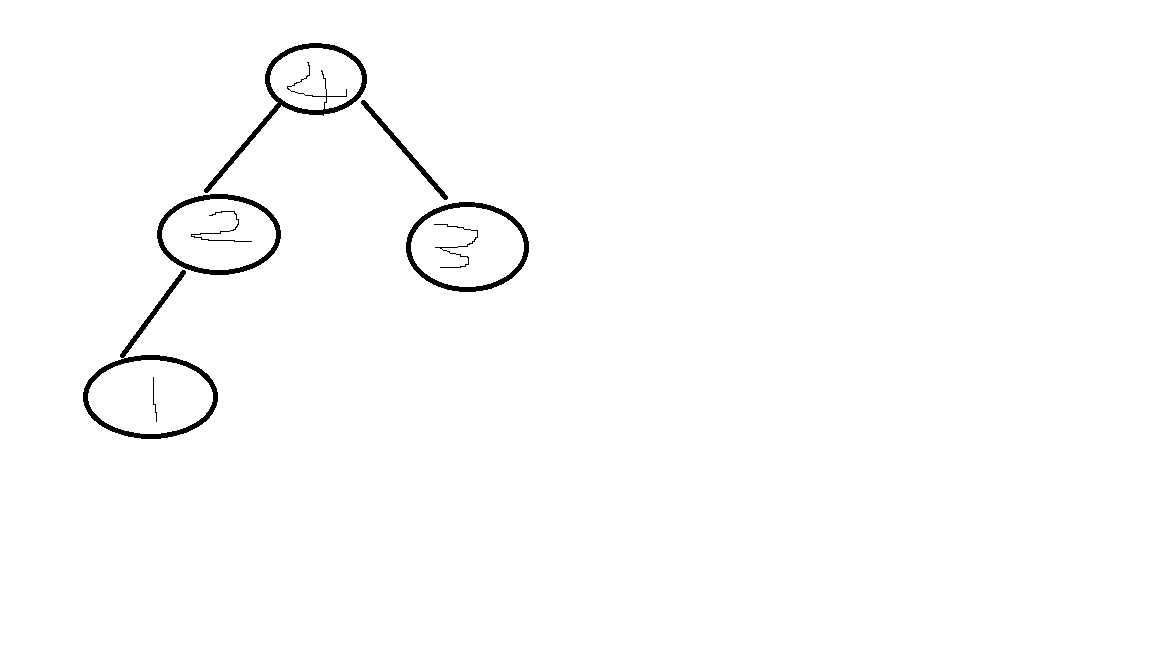
堆的操作

二叉堆的基本操作：插入，删除，查询。

1.插入

插入到根堆中首先默认插入到堆尾，

然后看上一层的父域是否比他小或者大（视情况最大堆或者最小堆而定），

用最大堆举例，如果父域大于要插入的堆，则它不需要变化，待在堆尾即可。

如果父域小于要插入的堆，则让他们两个交换继续判断，直到父域比他大或者到了堆顶。

代码

void    push(int x)    //x为要插入的数 
{
    int   now ,temp;   //now 存现在位置，temp寻找夫域
    data[++end]=x;  //将要插入的数放在堆尾
    now=end;             //当前堆的位置               
    while(now)    //判断是否是根节点
    {    
        temp=now>>1;//找到它的父域然后进行判断
        if(data[now]<data[temp])
        swap(&data[temp],&data[now]);//父域比要插入的小就交换 
        else break;//如果比它父亲小，那就代表着插入完成了 
        now=temp;//结束循环
    }
    return; 
}            

　2.删除

删除操作就是把莫个节点的位置放到堆底然后删除。

首先将需要删除的节点和堆底交换然后删除堆底，然后将互换的堆底进行判断使其符合二叉堆性质，

即交换的值，与根节点进行判断，满足要求就交换,否则结束。

代码：

void pop()
{
    swap(&data[1],&data[end]);
    end--;        //交换堆顶和堆底，然后直接删除堆底 
    int now=1，temp;
    while((now<<1)<=end)       //判断是否已经到堆底
{                                
        int temp=now<<1;      //找出当前节点的左儿子   temp+1就是右边儿子
        if(temp+1<=end&&data[temp+1]<data[temp])
        temp++;           //从左到右
        if(data[now]<data[temp])      //进行判断
        swap(&data[now],&data[temp]);
        else break;      //已经完成了 
        now=nxt;       //继续向下交换 
    }

}     

三 查询

查询就是看堆顶嗷，看一下堆顶就完事了。 heap[1].

STL实现。。。。未完待续

二叉堆

标签：bre   最大   图片   二叉树   12px   turn   bsp   操作   --   

原文地址：https://www.cnblogs.com/johnfllora/p/12270927.html