标签:需要 min src out har 处理 两种 编号 第一个
t1
初始有k个装备,每个装备n种属性,现在有q个操作(合成的装备编号为现在编号最大的装备编号+1,原装备不消失)
1 x y 将第x个和第y个装备每项属性取max合成一个新装备
2 x y 将第x,y个每项取min。
3 x y 询问第x个装备的第y项属性值。
n,q<=1e5 k<=12
题解
定义b[i][j]=1,j是一个状态,表示第i个装备可以对第j个状态中的所有装备的最小值,取max。
初始b[i]中所有包含(1<<i-1)的状态都为1。
先将每种属性里的装备从大到小排序。
1操作就将两个的b取|,表示可以这两种装备的所有可取状态都可以取。
2操作就是对两个的b取&,表示取最小值。
3操作,顺序枚举该属性的所有初始装备依次累加状态,第一个可以取得装备即为答案。
代码如下:

#include<bits/stdc++.h> using namespace std; const int N=1e5+5; int n,k,q; struct pigu { int id,val; }a[N][15]; bitset <5000> bi[N+20];//bi[i][j]=1表示可以取j状态的最小值 inline int read() { char c=getchar(); int x=0,f=1; while(!isdigit(c)) {if(c==‘-‘) f=-1;c=getchar();} while(isdigit(c)) {x=(x<<3)+(x<<1)+c-‘0‘;c=getchar();} return x*f; } inline bool cmp(pigu x,pigu y) { return x.val>y.val; } int main() { freopen("compose1.in","r",stdin); freopen("compose.out","w",stdout); n=read();k=read();q=read(); for(int i=1;i<=k;i++) bi[i].reset(); for(int i=1;i<1<<k;i++) for(int j=1;j<=k;j++) if(i&(1<<j-1)) bi[j][i]=1; for(int i=1;i<=k;i++) for(int j=1;j<=n;j++) { a[j][i].val=read(); a[j][i].id=i; } for(int i=1;i<=n;i++) sort(a[i]+1,a[i]+k+1,cmp); int tot=k; for(int i=1,x,y,z;i<=q;i++) { x=read();y=read();z=read(); if(x==1) { tot++; bi[tot]=bi[y]|bi[z]; } if(x==2) { tot++; bi[tot]=bi[z]&bi[y]; } if(x==3) { int now=0,ans=0; for(int j=1;j<=k;j++) { now|=(1<<a[z][j].id-1); ans=max(ans,a[z][j].val*bi[y][now]); } cout<<ans<<"\n"; } } }
t2
给出n*n 01矩阵A和n维向量b,每次读入x询问 A^{x} *b
50分做法。
先预处理出2^{n} 的矩阵乘积,查询时就只需要向量乘矩阵,每次只需要n方即可。
复杂度预处理n^{3} log_2{k}+q*n*n*log_2{k}。
100分做法。
好像可以用bitset优化再翻转矩阵行列,还要先判断每一位是否为1在乘行列。
不知道能不能过
莫得代码
t3
最后答案显然就是 \sum 全部变为某种颜色的期望步数乘以变为该种颜色的概率,设p[i]表示现在有i个这样的颜色到得手的概率,f[i]为现在有i个的期望步数。
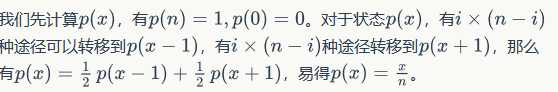

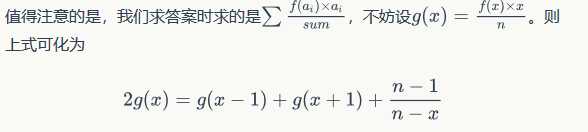
知道了g[n]和g[0],如果知道了g[1]就舒服了,
然后就求g[1],然后反手就被发现了一个性质

然后线性递推即可。
代码如下:

#include <algorithm> #include <cstdio> typedef long long ll; inline int read(){ char c=getchar(); int x=0,ft=1; for(;c<‘0‘||c>‘9‘;c=getchar()) if(c==‘-‘) ft=-1; for(;c>=‘0‘&&c<=‘9‘;c=getchar()) x=x*10+c-‘0‘; return x*ft; } const int mod=1e9+7; inline int fpow(int x,int k){ int res=1; for(;k;k>>=1,x=(ll)x*x%mod) if(k&1) res=(ll)res*x%mod; return res; } const int N=1e5+5; int n,a[2005],sum,lim,f[N],ans; int main(){ freopen("hard.in","r",stdin); freopen("hard.out","w",stdout); n=read(); for(int i=1;i<=n;++i){ lim=std::max(lim,a[i]=read()); sum=(sum+a[i])%mod; } f[1]=(ll)(sum-1)*(sum-1)%mod*fpow(sum,mod-2)%mod; for(int i=1;i<lim;++i){ int g=(ll)(sum-1)*fpow(sum-i,mod-2)%mod; f[i+1]=(((ll)2*f[i]-f[i-1]-g)%mod+mod)%mod; } for(int i=1;i<=n;++i) ans=(ans+f[a[i]])%mod; printf("%d\n",ans); fclose(stdin); fclose(stdout); return 0; } /* 4 2 1 5 7 */
标签:需要 min src out har 处理 两种 编号 第一个
原文地址:https://www.cnblogs.com/betablewaloot/p/12271236.html