标签:结果 参数 line 一个 重要 sof 初始化 splay 隔离
概率传播
简单的模型:
第一波:一个携带病毒的人进入人群,与他接触的人有概率q被感染,他接触了d个人,d中一部分将会被干扰
第二波:d人活动,会见d个人,开始传播
后续:上述重复
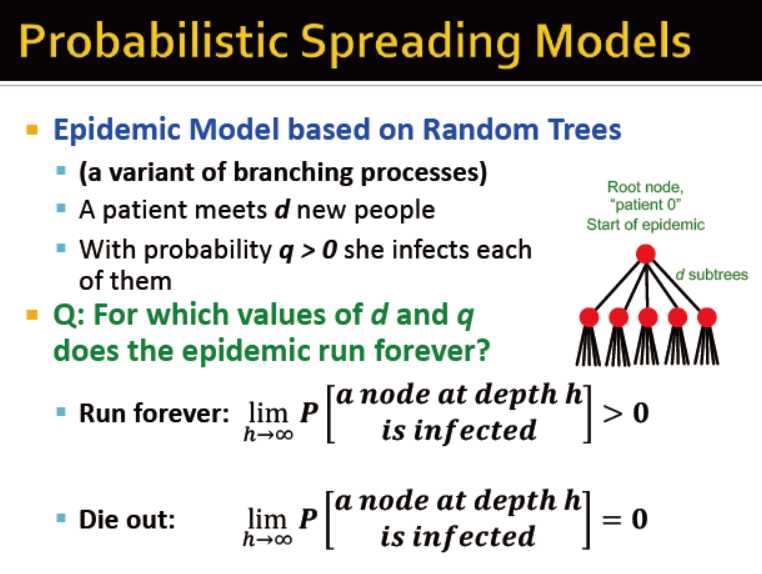
基于随机树的传播
那么,当d和q等于什么值的时候,传染病会永久传播?
Ph 节点a在第h层被感染的概率
具体公式如下:
x 节点a在第h-1层被感染的概率,从x=1开始,因为p1=1
f(x) 节点a在第h层被感染的概率
q 感染概率
d 度
若想传染病灭绝,那个f(x)的曲线必须在y=x之下
R0=q*d=受感染人数的期望 在传染人数
当R0>=1时,成为传染病
当R0>=1时,成为传染病
当<1时,疾病灭绝
抑制扩散的措施
改变q或d
减少d:隔离人
减少q:鼓励更好的卫生习惯用于较少疾病传播
HIV的R0在2到5之间
Measles的在12到18
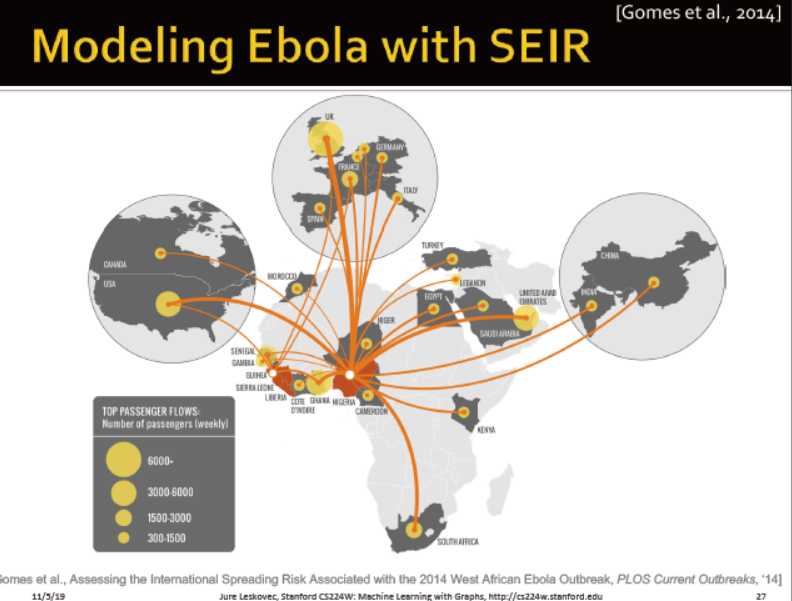
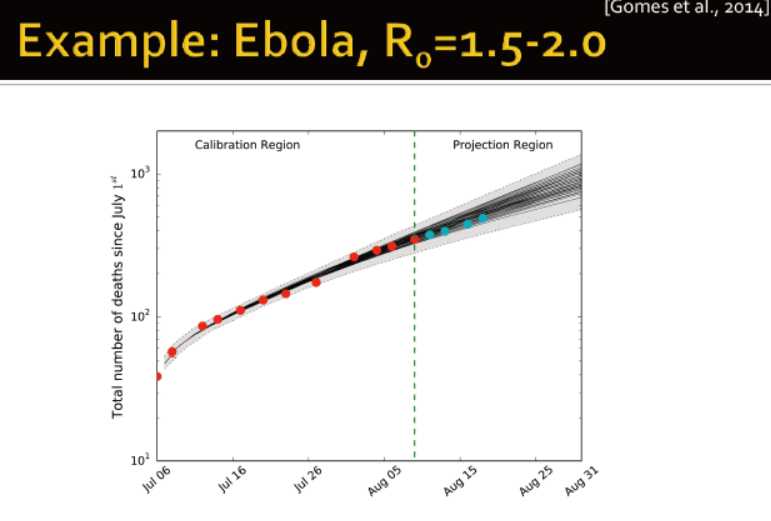
Ebola的在1.5到2
应用:Flickr的级联 和 真实疾病的R0评估
首先来看Flickr的
在Flickr的社交网络中,用户与其他用户通过成为好友相连,一个用户可以点赞一个图片
数据:
100天的照片点赞
用户数量:两百万
点赞数:34734221
照片数:11267320
Flickr中的级联
一个用户在他至少一个好友点赞一个照片后也点赞该照片
从真实数据中计算R0
首先计算q
然后根据公式计算R0
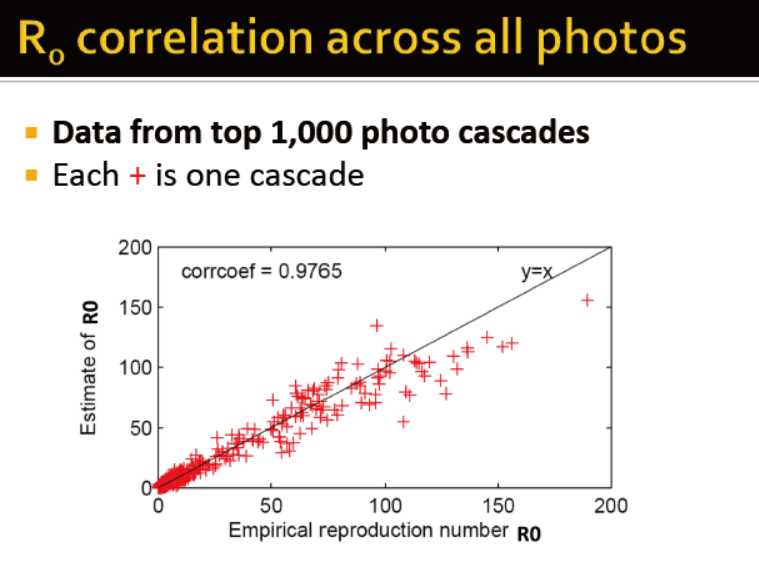
此处有两个R0,评估的R0通过公式计算而得,经验主义的R0通过数直接相连的节点的被传染的数量
在Flickr中,R0在1到190,比很多传染病的都要高,这说明,信息在社交网络中的传播非常迅速
传染病模型
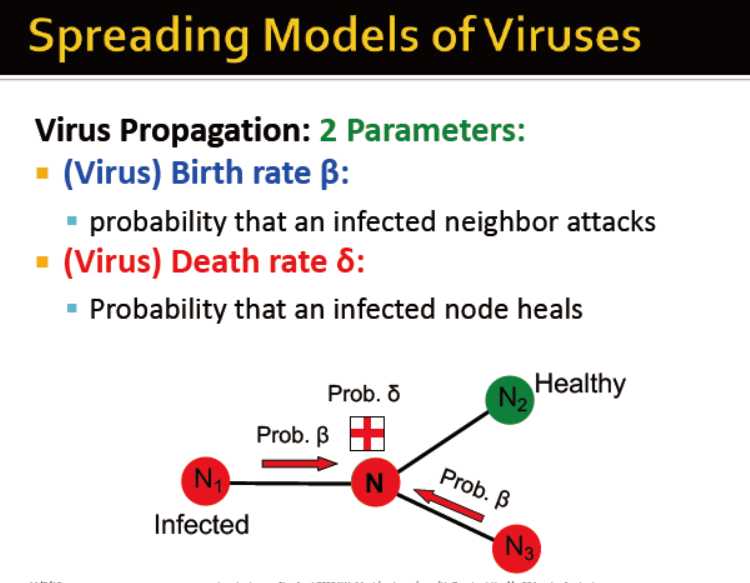
病毒传播设计的两个参数:
被感染概率:β
被治愈概率:δ
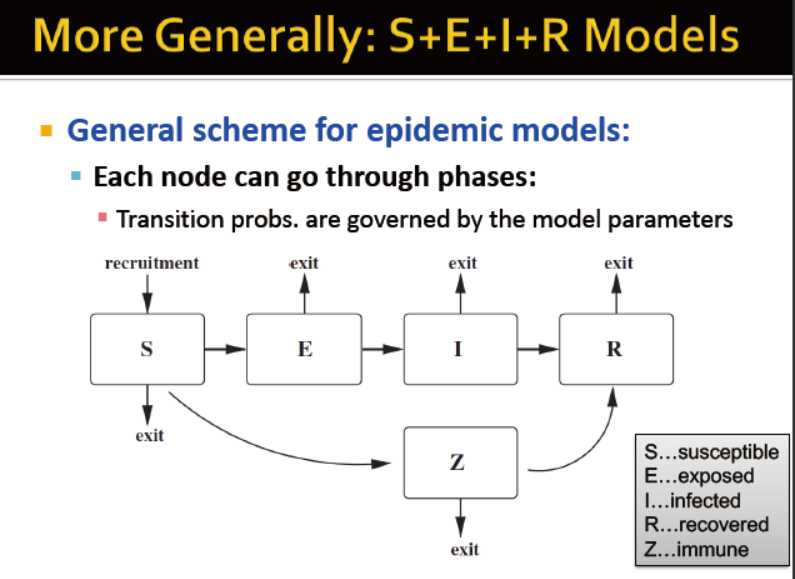
更普遍的:S+E+I+R模型
传播模型受以下参数控制
S:易感人群
E:暴露人群
I:受感染
R:痊愈
Z:免疫者
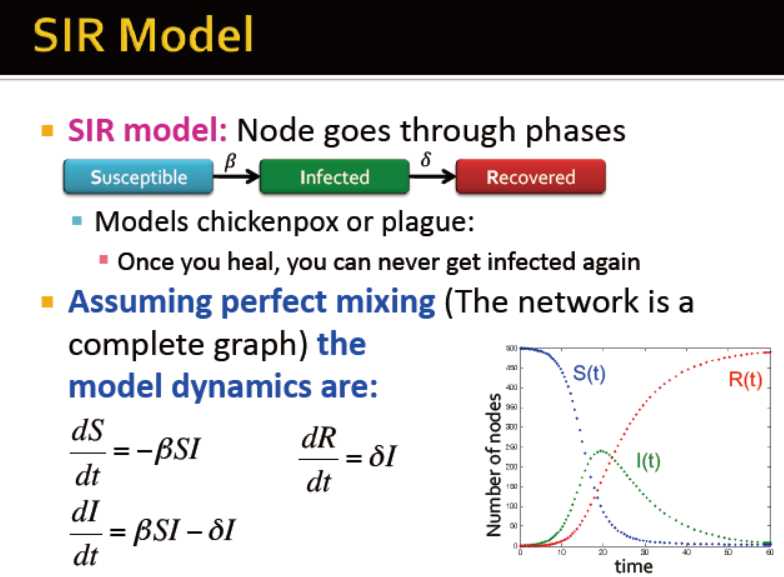
SIR模型
需要注意的一点:当一个感染者被治愈后,就不会再被感染
假设网络是一个完全图,模型的动力学相关的公式如下:
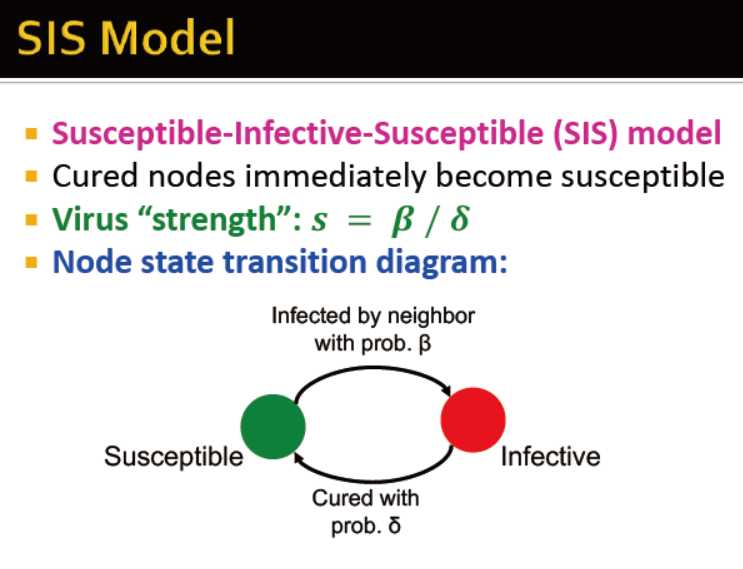
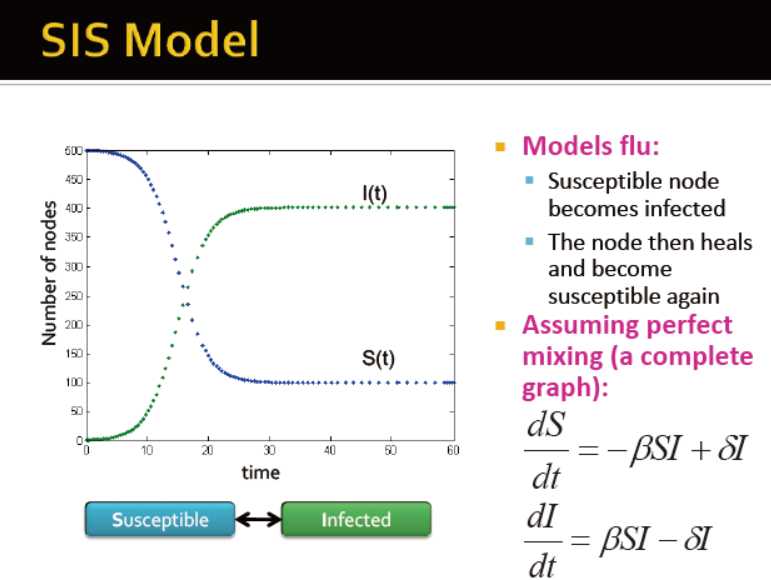
SIS模型
治愈的节点会被重复感染
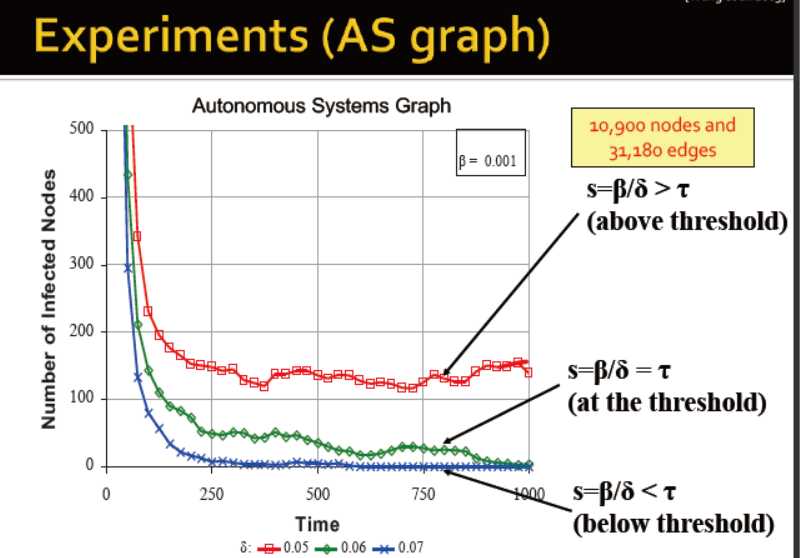
参数:病毒力量 s=β/δ
传播阈值t 当s<t时,病毒可以灭绝
给定一个网络,那么,他的阈值是?
阈值为邻接矩阵的最大特征值
初始感染人数对于最终的传播结果重要吗?
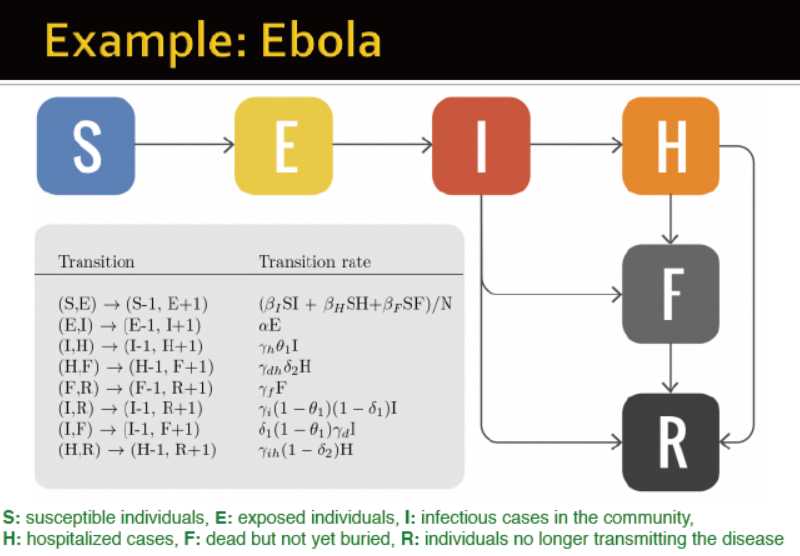
埃博拉的模型:
S:易感人群
E:暴露人群
I:受感染
Z:免疫者
H:住院病例
F:死亡但没有被掩埋
R:不传播该疾病的个体
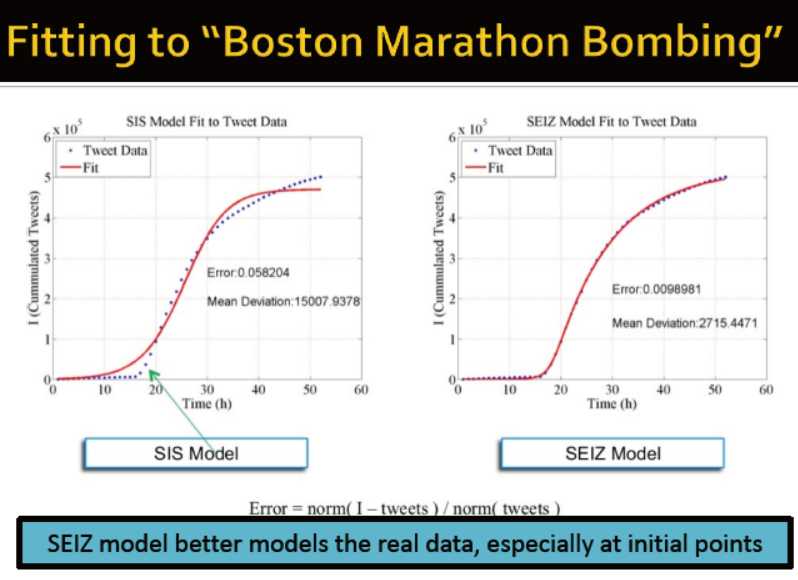
使用SEIZ模型模拟谣言传播
S: 易感人群→twitter的用户
I: 受感染者→相信谣言的人,发了相关的tweet
E:暴露者→看到谣言但未相信的人群
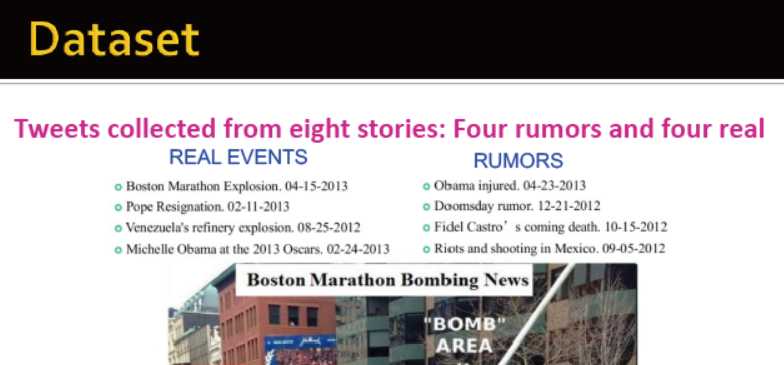
数据集:收集了4个故事,其中4真4假
将数据应用到SEIZ模型
tweet(t)=谣言的tweet数
I(t)=模型评估的谣言tweet
使用网格搜索发现最优参数
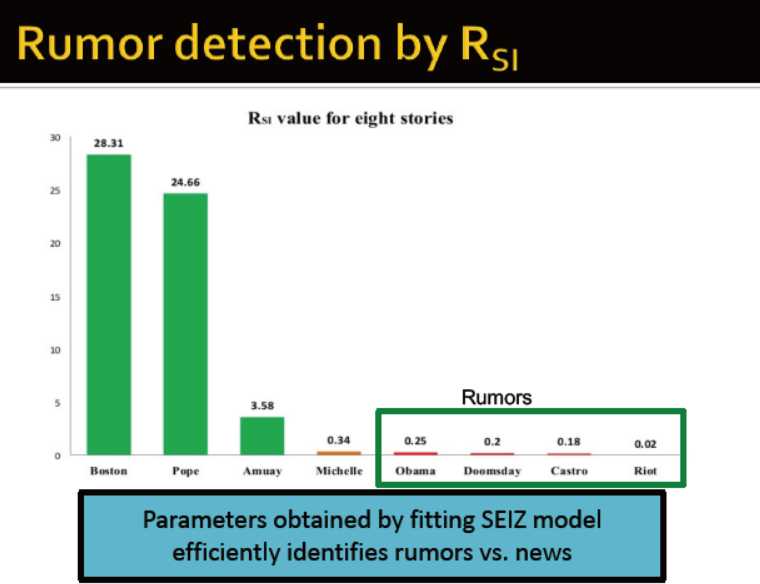
谣言的Rsi值较小
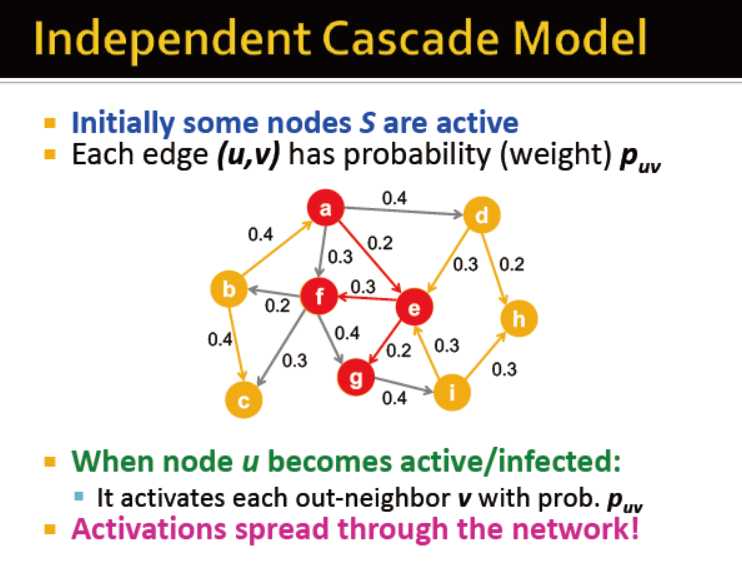
独立的级联网络初始化一些节点是毁约的,每条边有一个概率权重
当一个节点被感染的时候,传染给邻居的概率为p_uv
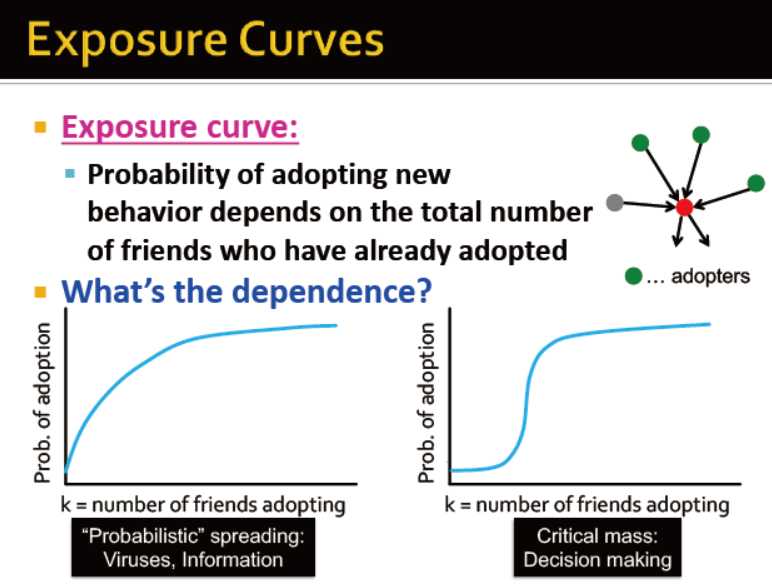
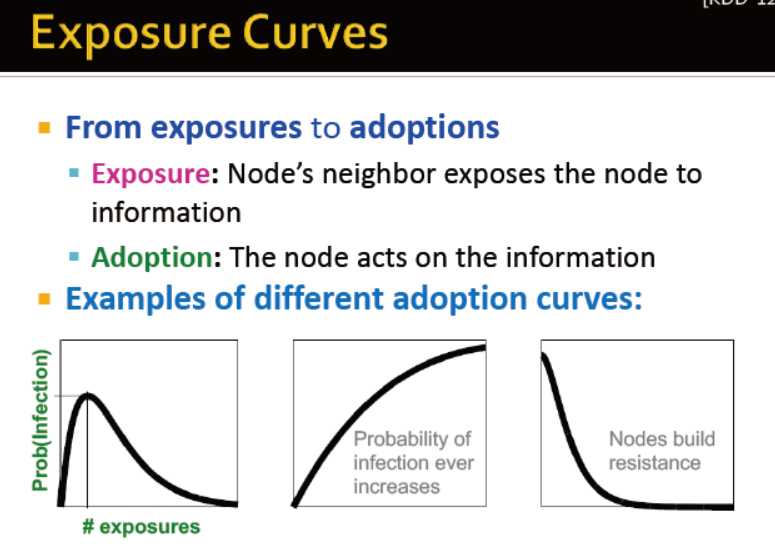
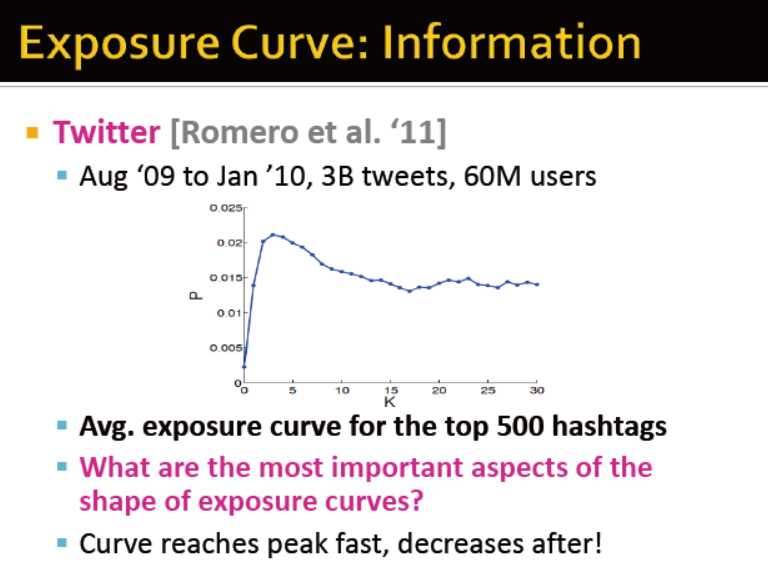
从暴露到采用
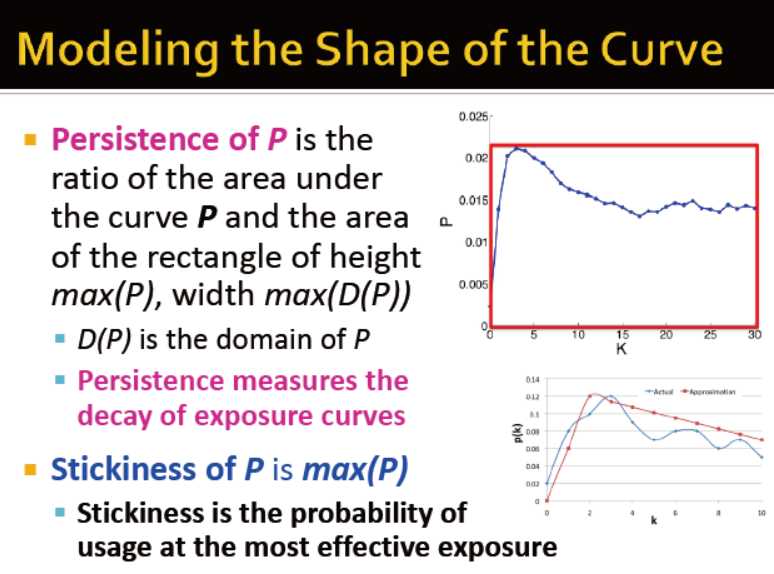
从两个曲线图中可以看出,受影响做决策与疾病传输的区别:
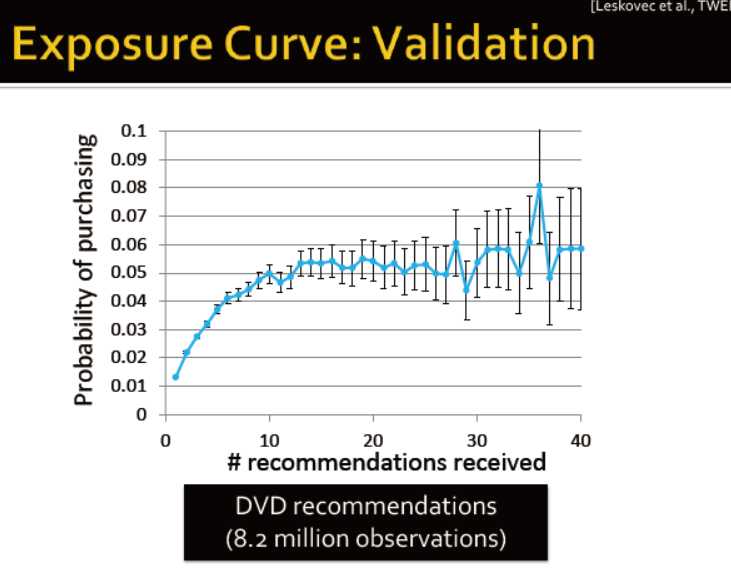
在病毒式营销中的扩散
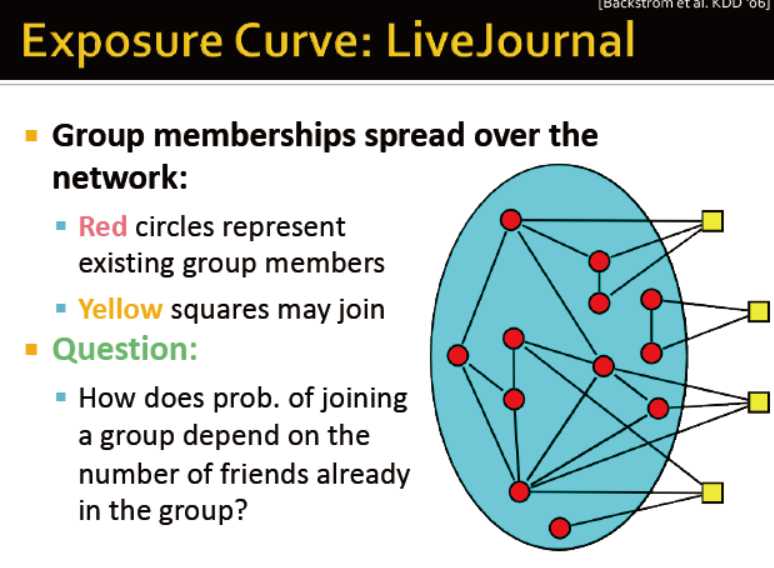
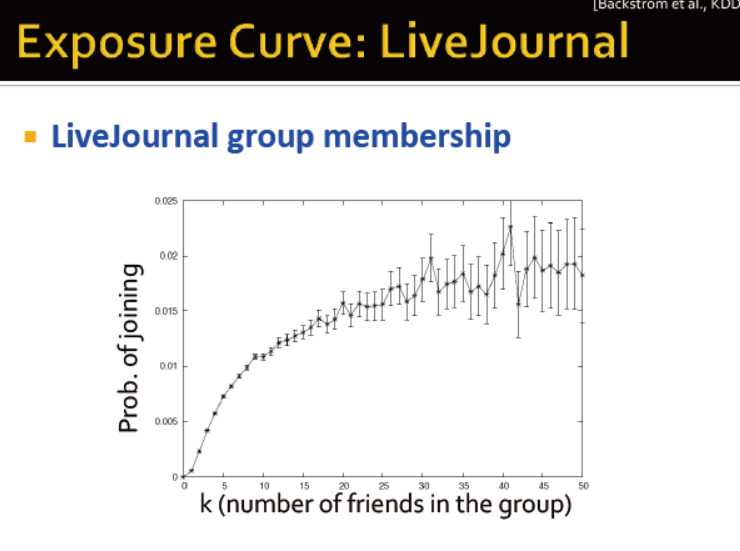
交友网的例子:朋友在一个圈子的概率是如何决定一个人是否加入某个圈子的?
13-contagion 图机器学习之疾病的概率传染
标签:结果 参数 line 一个 重要 sof 初始化 splay 隔离
原文地址:https://www.cnblogs.com/combfish/p/12271503.html