标签:one title range 最优 最大 时间复杂度 img 营销 vertica
网络的影响力最大化
与陌生人相比,我们更容易受到朋友的影响
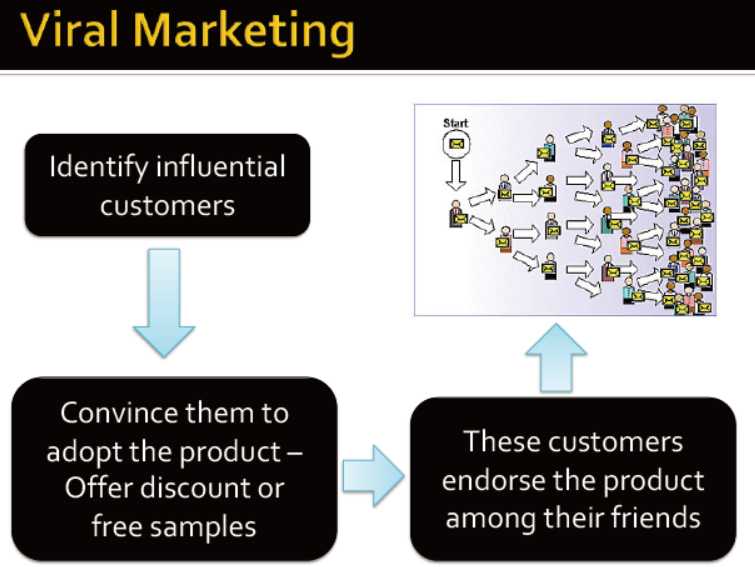
病毒性营销
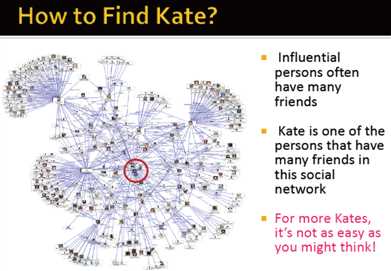
凯特王妃的影响力
凯特穿过的衣服容易脱销
那么,如何发现类似于凯特这一号人物的类似节点?
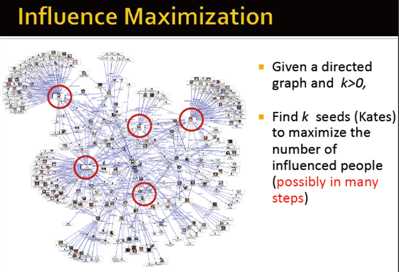
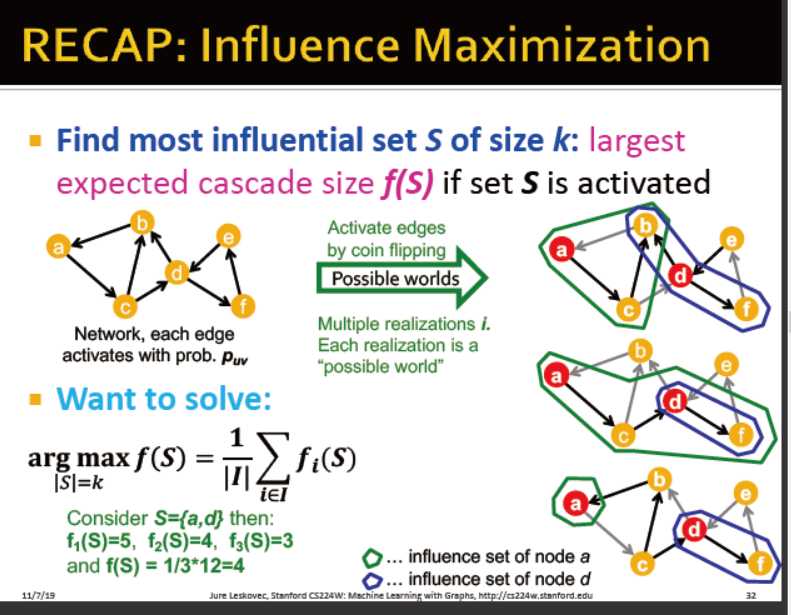
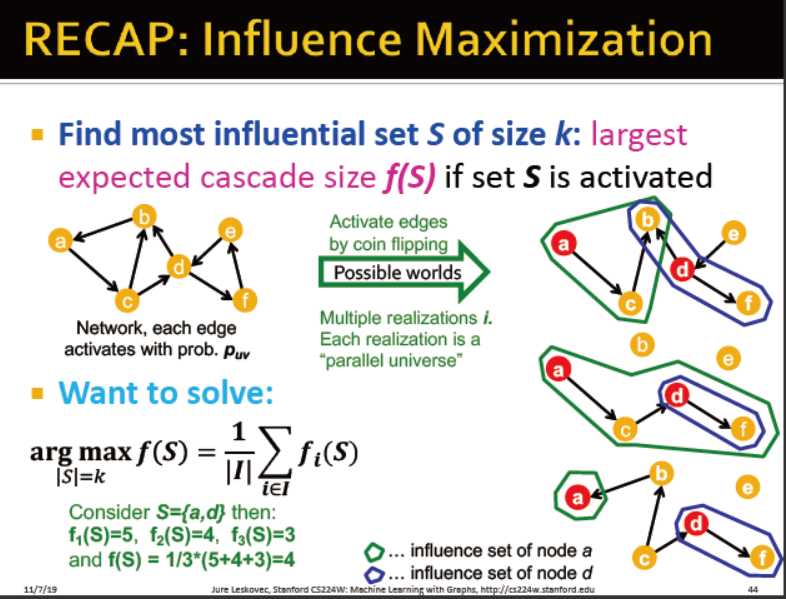
影响力最大化
给定一个有向图,找到k个影响力最大的种子
两个经典的传播模型
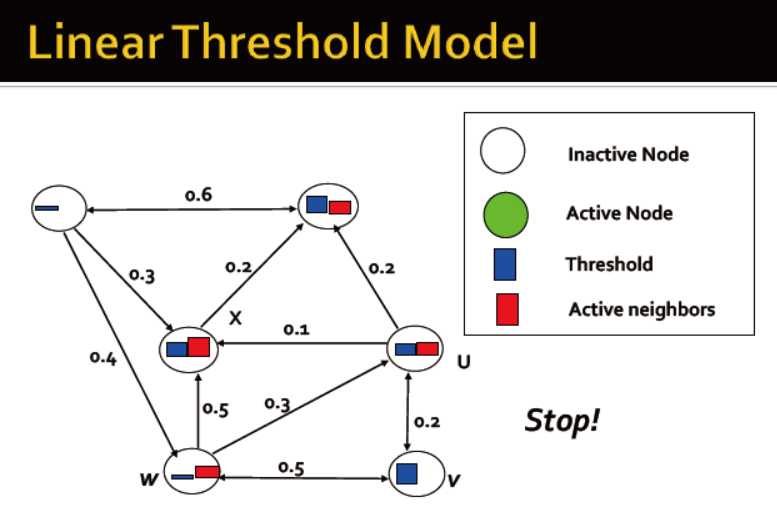
线性阈值模型
独立级联模型
首先来看线性阈值模型
节点v有随机的阈值 0到1
节点v受邻居w的影响,影响范围为b_v,w
当节点受影响的权重和大于某个阈值时,被激活
概率传播
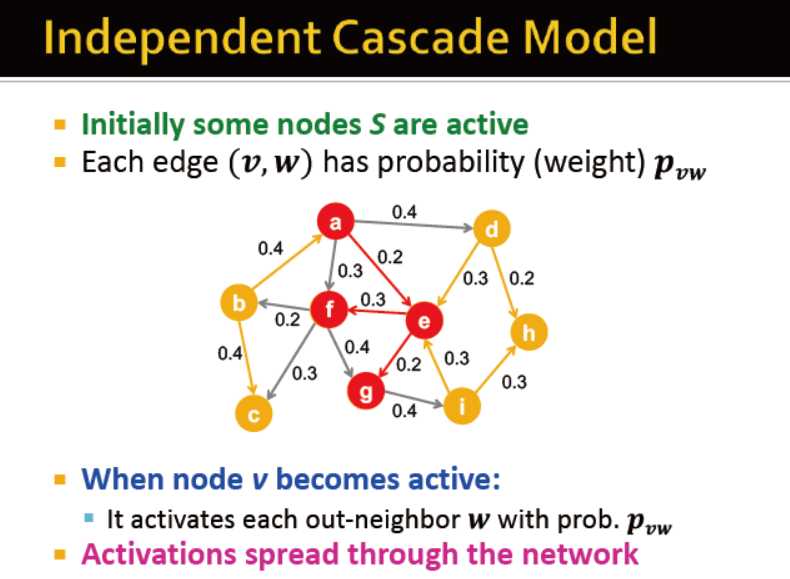
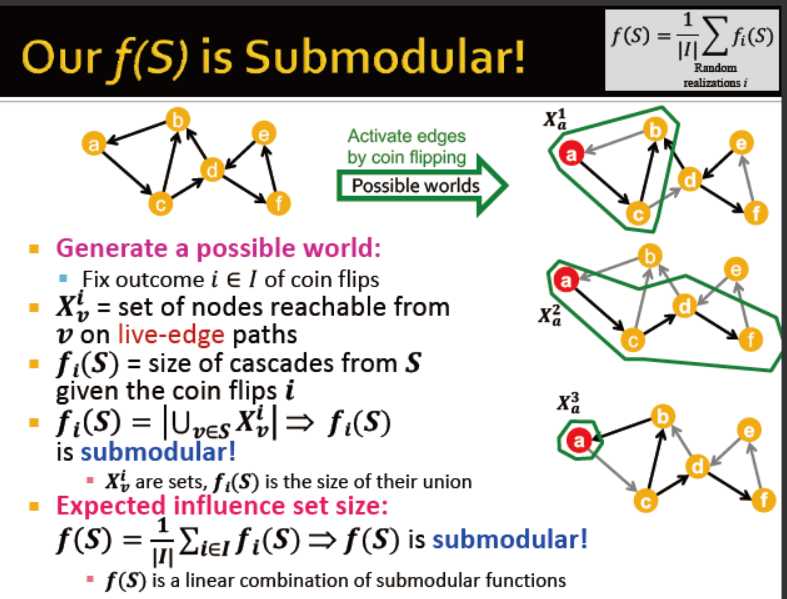
独立级联模型
有向图
每条边(v,w)有一个属性是概率p_vw,表示,若v是激活的,那么,他使w激活的概率为p_vw
每条边最多只能触发一次
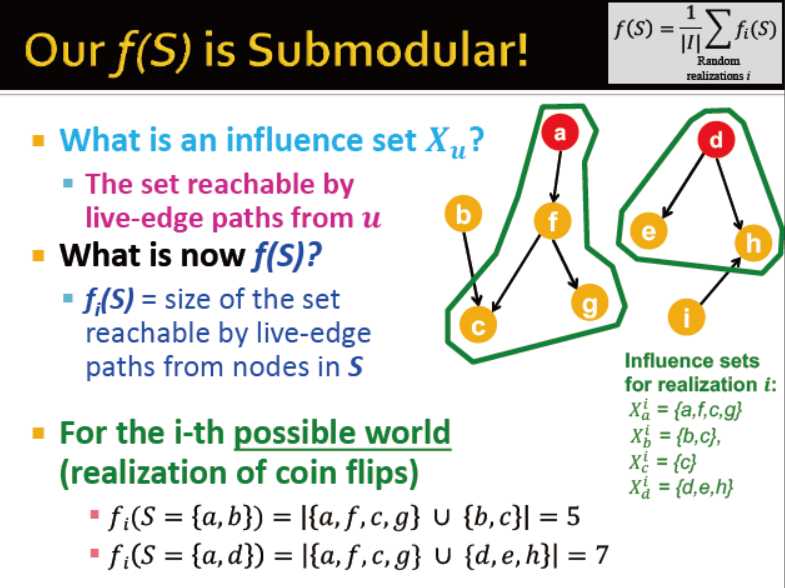
f(s): 最终活跃的集合
f(s)越大,S越具影响力
影响力最大化的难题
近似算法:
不需要找到全局最优的解决方案
近似算法:贪心爬升算法
输入:收到影响的集合Xu,内含若干节点{v1,v2,..}
算法:每一次迭代,激活节点u后,带来的最大激活增益
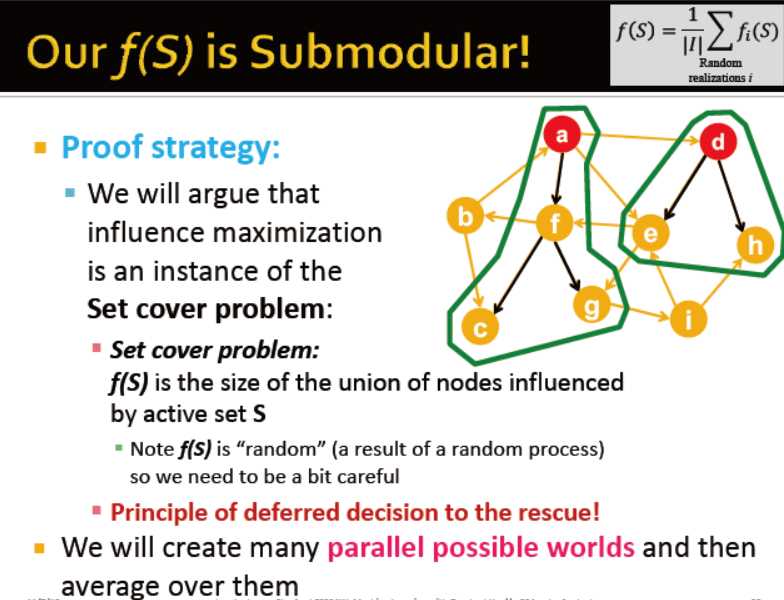
计划:证明两件事情:f(s)是子模块? ;算法给了一个近似优化的解决方案
实验数据:共同协作写论文的网络,来源 arXiv
级联过程示例:新科技方法/研究领域的传播
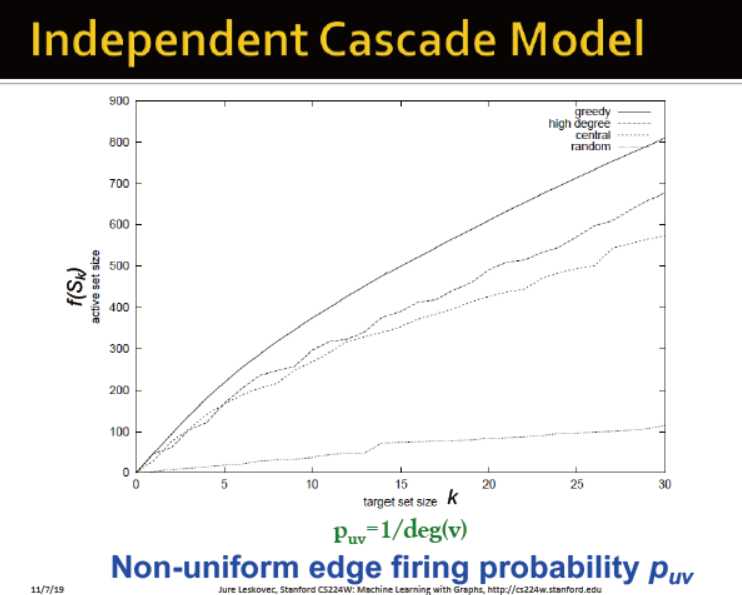
独立级联模型
每个用户的阈值归一化到[0,1]
case1:每个边都一个统一的概率p
case2:每个边(v,w)激活w的概率p等于1/deg(w)
与3个结果进行比较:度中心性;紧密中心性;随机节点
加速:基于骨架的算法
为了计算影响力最大化,我们需要
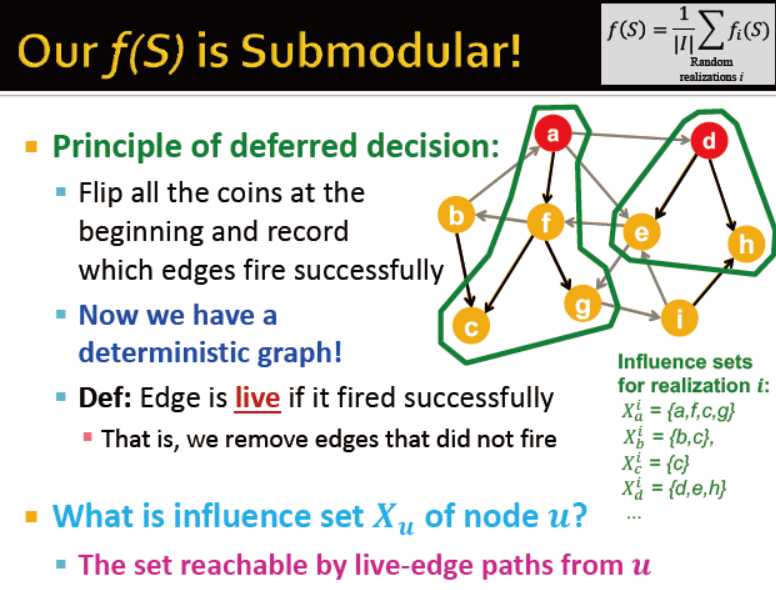
1) 生成R个可能的世界
2) 识别K个具有影响力的节点
时间复杂度为O(m) m为边的数目
基于骨架的算法,可将复杂度缩至O(1)
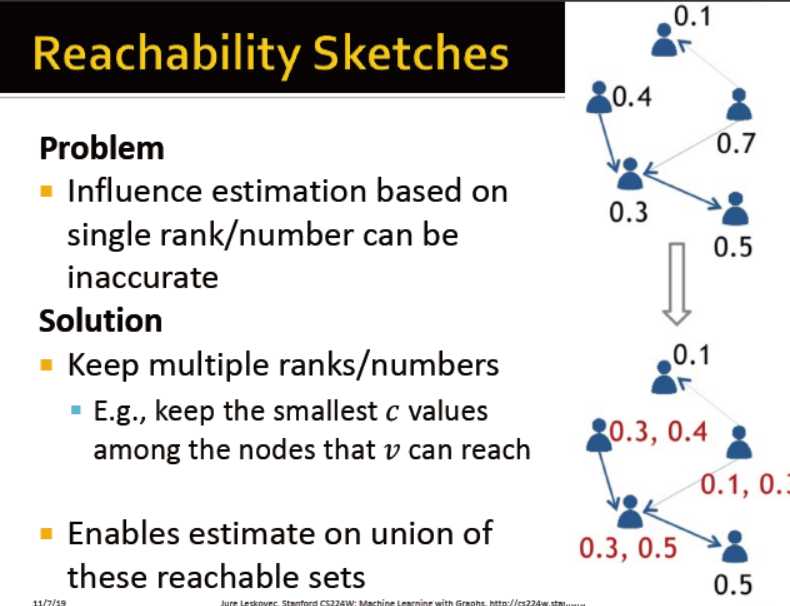
计算每个节点的小架构来评估影响力
再使用计算结果计算影响力最大化
14-influence 图机器学习之网络的影响力最大化
标签:one title range 最优 最大 时间复杂度 img 营销 vertica
原文地址:https://www.cnblogs.com/combfish/p/12271507.html