标签:历史 未来 证券 sse 好的 图片 包含 api 存在
一、CAPM与确定一致预期收益率
风险和预期收益率是主动投资管理中最重要的两个部分,讨论预期收益率最好从认识资本资产定价模型(Capital Asset Pricing Model,CAPM) 开始。CAPM模型由Sharpe(1964)建立,Treynor(1961)、Lintner(1965)和Mossin(1966)在同期也做了相关的研究,在CAPM看来,主动投资管理是存在质疑的,但是它有一个重要的意义就是一套用来确定一致预期收益率的步骤从而为我们设定了比较基准,同时CAPM发展出来的很多分析方法可以转用于主动量化投资。
CAPM不是确定一致预期收益率的唯一方法,还有两种可以替代的方法:第一种方法是使用历史平均收益率,但是它的问题在于太过于静态以至于包含了大量了样本误差以及忽视了股票空间(退市、合并、上市等)和股票本身(盈利、资本结构、波动等)随着时间的变化;第二种方法是APT模型,但是后面会提到,APT模型是主动投资经理的一个有效工具但是不能作为一致预期收益率的来源。而CAPM则可以被认为是确定一致预期收益率最好的方法,自提出以来经受住了学界和业界的无数考验。
二、均值方差分析:有效前沿和市场组合
(一)两个特征组合:最小风险组合和最大夏普比率组合
上一篇系列笔记中的特征组合,首先构建一个关于e的特征组合,它就是最小风险组合。


然后构建另外的一个特征组合(最大夏普比率组合)。

(二)有效前沿与特征组合

(三)市场组合——也是最大夏普比率组合

三、收益率和风险分解
CAPM基于两个构想:
第一个是市场组合。理论上市场组合是我们均值方差分析的内容,且应该包含所有的资产(除了股债汇金期币等,还应该包括一些实业投资),在实践中一般选取覆盖面广的指数(这种指数一般就是通过均值方差分析做出来的);
第二个是将所有资产或组合与市场相联系的β系数。一个组合P的贝塔是:组合P和市场组合M的超额收益率的协方差,除以市场组合的方差;市场组合的β为1,无风险资产组合的β为0;虽然β是一个先验的概念,但是其来自于对同期的组合超额收益率和市场超额收益率做线性回归,是我们对未来一期的贝塔所作出的预测,当然我们有更好的做法,比如Rosenberg(1985)发现贝塔具有均值回归的特点(类似于反转效应),也可以通过资产贝塔法(使用公司的基本面数据,参考行业数据来对权益贝塔进行更加普适化的估计)来对β进行估计,除此之外也可以通过对历史贝塔进行贝叶斯调整。

基于此,我们可以将一个组合超额收益率分解为一个与市场完全相关的部分和一个与市场不相关的部分,甚至不需要对市场组合M作任何假设,它在这里可以是任意一个其他组合。CAPM认为任何组票或者组合的预期残差收益率等于0(非常严格),这意味着组合P的预期超额收益率完全由市场组合的预期超额收益率和组合的β决定。
CAPM认为,市场风险是每个投资者都会承担的风险(系统性风险),投资者会因为承担市场风险而获得收益上的补偿,但是残差风险则是投资者自主承担的,所有投资者都可以通过组合的分散化来规避残差风险,但是如果有投资者承担了残差风险,例如两类投资者在做多和做空的对象不一致,那么一方残差收益率为正,另一方残差收益率必然为负。也就说,如果你不具备信息优势,那么你应该持有市场组合选择被投投资方法,这也是为什么市场上指数投资的规模发展快速的原因。
四、预期收益率与投资组合
在均值方差分析框架下,我们可以通过优化求解得到市场组合,并选择市场组合和无风险资产的再组合,如果我们限定在全额投资中优化,那么我们将得到市场组合和最小方差组合的再组合。如果在我们得到市场组合(一致组合)后假定它是最优的,那么我们可以得到它的预期收益率(也是CAPM产生的预期收益率),我们称之为一致预期收益率。
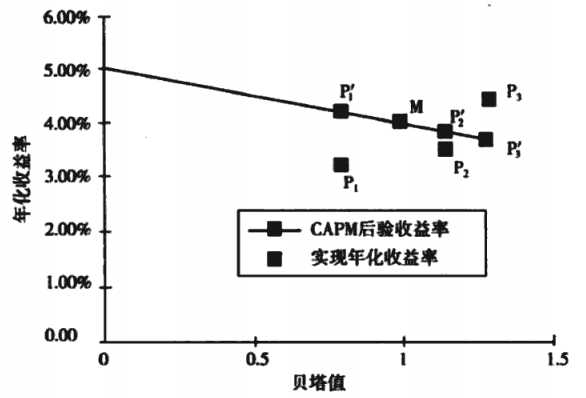
我们可以得到证券市场线(Security Market Line,SML),可以通过判断组合的实际收益(后验)与组合的预期收益率(先验)的差来判断一个投资经理是否创造了附加值。
标签:历史 未来 证券 sse 好的 图片 包含 api 存在
原文地址:https://www.cnblogs.com/amosding/p/12274359.html