标签：problem tco nal 路径搜索 each top ott different value
In an N by N square grid, each cell is either empty (0) or blocked (1).
A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:
C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)C_1 is at location (0, 0) (ie. has value grid[0][0])C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.
Example 1:
Input: [[0,1],[1,0]]
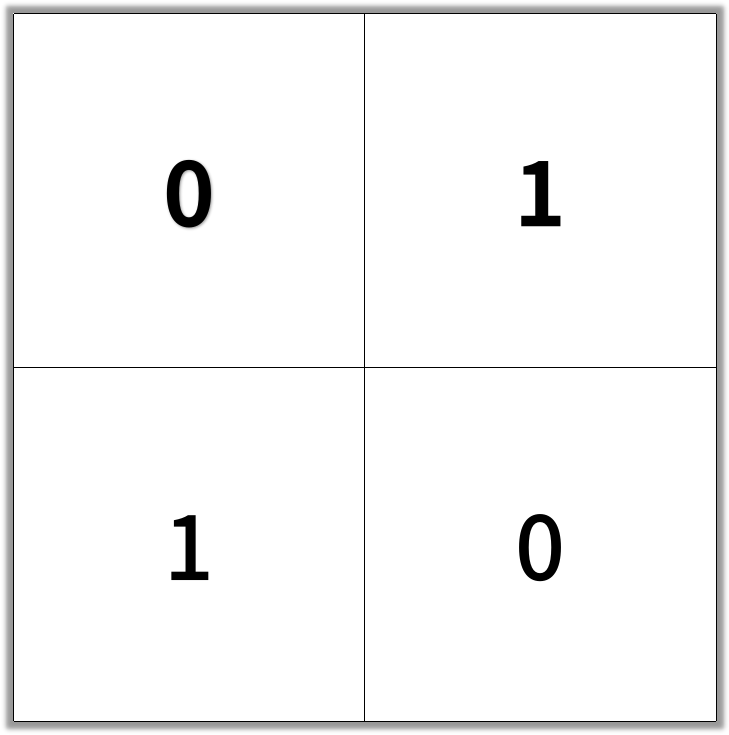Output: 2
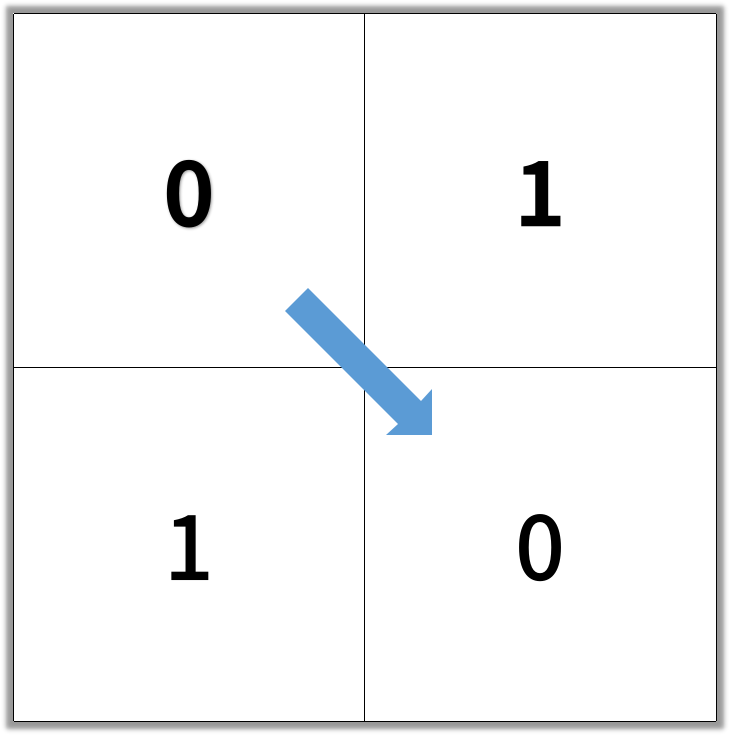
Example 2:
Input: [[0,0,0],[1,1,0],[1,1,0]]
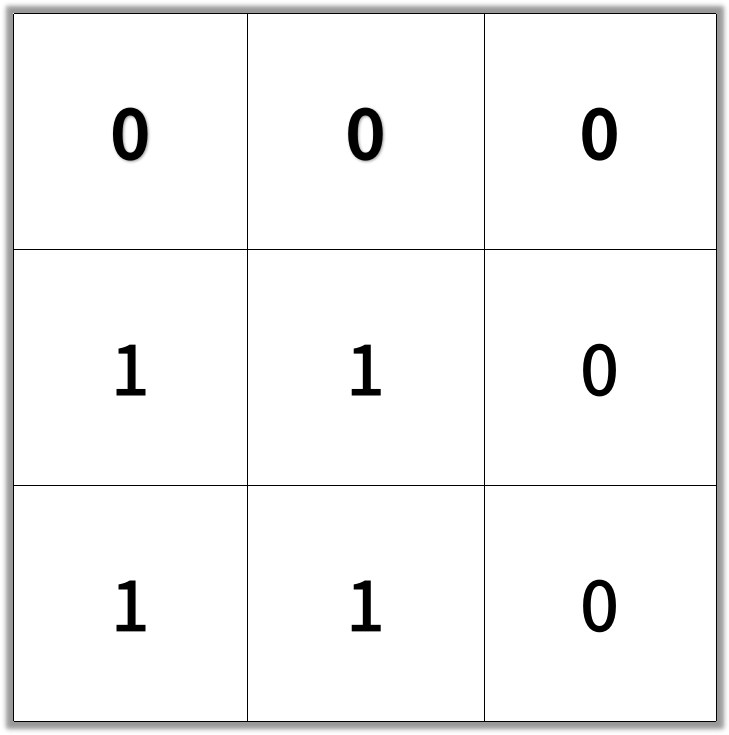Output: 4
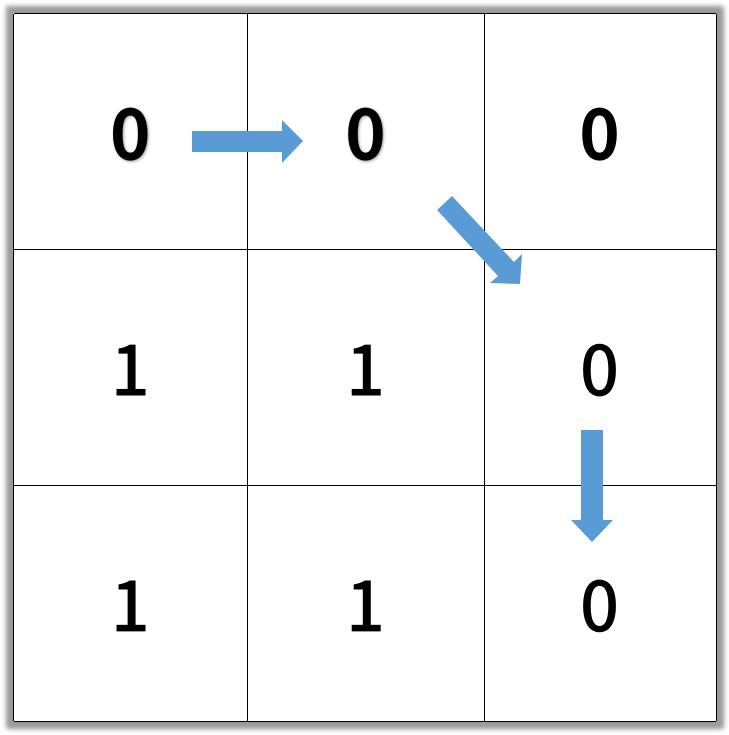
Note:
1 <= grid.length == grid[0].length <= 100grid[r][c] is 0 or 1简单来说就是经典的BFS路径搜索，从左上角走到右下角，0是通路，1是障碍。
先给出最简洁的写法：
class Solution: def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int: n = len(grid) if grid[0][0] or grid[n-1][n-1]: return -1 record = [(0,0,1)] for i, j, d in record: if i == n-1 and j == n-1: return d for x, y in ((i-1,j-1),(i-1,j),(i-1,j+1),(i,j-1),(i,j+1),(i+1,j-1),(i+1,j),(i+1,j+1)): if 0 <= x < n and 0 <= y < n and not grid[x][y]: record.append((x, y, d+1)) grid[x][y] = 1 return -1
用 record 这个list来记录状态，然后直接一边在后面不停加上下一层的记录，一边iterate
注意到 由于是BFS，采用将已经过的grid置为1来避免重复访问（BFS才能这样做）
即便如此简洁，此方法还是有一些问题，因此更好的方法为：
class Solution: def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int: if not grid or grid[0][0] or grid[-1][-1]: return -1 m, n = len(grid), len(grid[0]) front, end, level = set([(0, 0)]), set([(m-1,n-1)]), 1 while front: # intersection if front & end: return level for x, y in front: grid[x][y] = 1 front = set((x+dx, y+dy) for x, y in front for dx, dy in [(1,1),(1,-1),(-1,1),(-1,-1),(0,1),(0,-1),(-1,0),(1,0)] if 0<=x+dx<m and 0<=y+dy<n and grid[x+dx][y+dy]==0) level += 1 if len(front) > len(end): front, end = end, front return -1
此方法解决了两个问题：
1. 更新每一层存的状态，减小内存空间
2. level只需一个变量存就够了（因为是BFS）
注意其采用了set而不用list，可以减少重复情况带来的重复计算
参考：
https://leetcode.com/problems/shortest-path-in-binary-matrix/discuss/312827/Python-Concise-BFS
BFS 基础写法 —— 以 LeetCode #1091 Shortest Path in Binary Matrix 为例
标签：problem tco nal 路径搜索 each top ott different value
原文地址：https://www.cnblogs.com/sbj123456789/p/12275446.html
