标签:ups map ring mat == bin scanf span div
前置知识
(1)如果将 aa 自乘一次,就会变成 a^2a2 。再把 a^2a2 自乘一次就会变成 a^4a4 。然后是 a^8a8…… 自乘 nn 次的结果是 a^{2^{n}}a2n 。对吧……
(2)a^xa^y = a^{x+y}axay=ax+y,这个容易。
(3)将 bb 转化为二进制观看一下:
比如 b = (11)_{10}b=(11)10? 就是 (1011)_{2}(1011)2? 。从左到右,这些 11 分别代表十进制的 8,2,18,2,1。可以说 a^{11} = a^8 × a^2 × a^1a11=a8×a2×a1。
为什么要这样表示?因为在快速幂的过程中,我们会把 aa 自乘为 a^2a2,然后 a^2a2 自乘为 a^4a4……像上面第一条说的。
取余运算有一些好用的性质,包括:
(A+B) \mod b = (A \mod b + B \mod b) \mod b(A+B)modb=(Amodb+Bmodb)modb
(A×B) \mod b = ((A \mod b) × (B \mod b)) \mod b(A×B)modb=((Amodb)×(Bmodb))modb
#include<iostream> #include<cstdio> #include<string> #include<algorithm> #include<queue> #include<set> #include<map> #include<cmath> const double PI = acos(-1.0); #define INF 0x3f3f3f3f typedef long long ll; using namespace std; ll quickPower(ll a, ll b,ll m) { //计算a的b次方 ll ans = 1; ll base = a; while (b) { if (b & 1) { ans *= base; ans %= m; } base *= base; base %= m; b >>= 1; //注意是b>>=1 not b>>1 } return ans; } int main() { ll b, p, k; scanf("%lld%lld%lld", &b, &p, &k); printf("%lld^%lld mod %lld=%lld",b,p,k,quickPower(b, p, k) % k); return 0; }
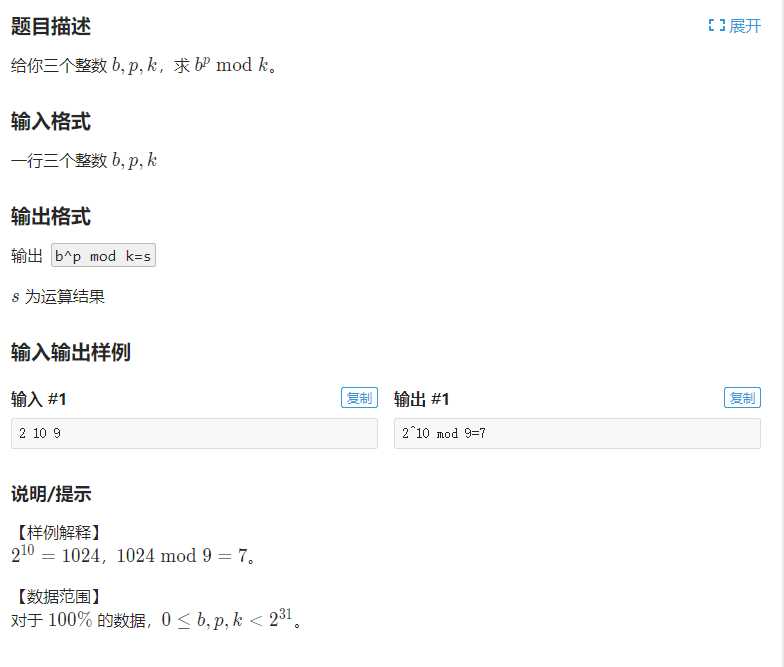
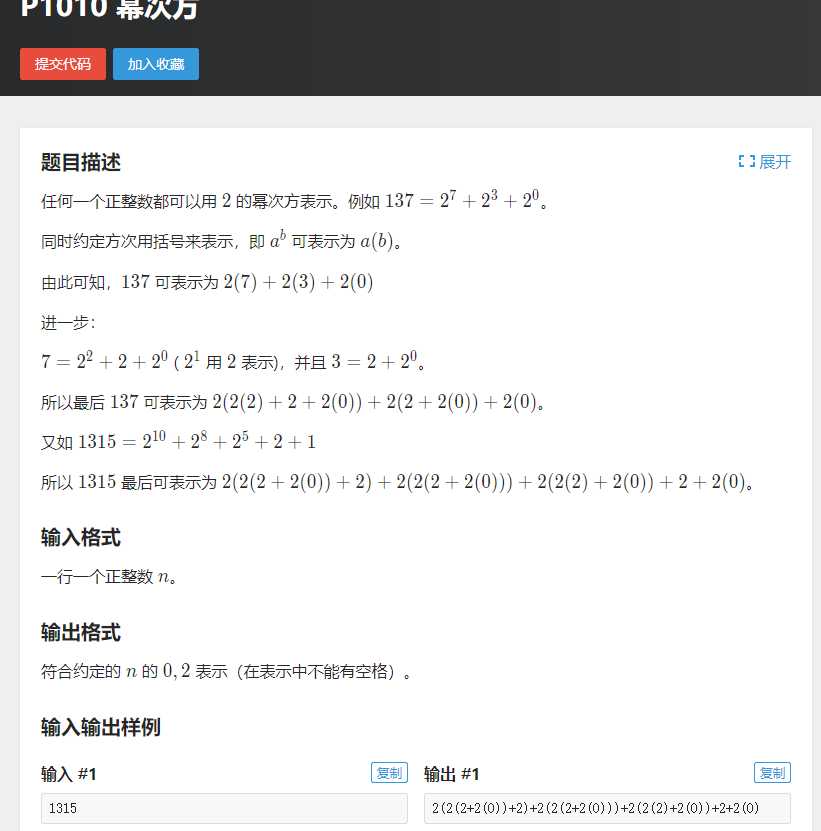
洛谷 1010 幂次方
string run(int x, int i = 0, string s = string("")) { if (!x) return string("0"); do if (x & 1) s = (i == 1 ? "2" : "2(" + run(i) + ")") + (s == "" ?"": "+") + s; while (++i, x >>= 1); return s; } int main() { int x; scanf("%d", &x); printf("%d", run(x)); return 0; }
太酷了
标签:ups map ring mat == bin scanf span div
原文地址:https://www.cnblogs.com/hznumqf/p/12283516.html