分治FFT

时间：2020-02-09 18:10:58 阅读：57 评论：0 收藏：0 [点我收藏+]

标签：shu make 复杂度 uil memcpy ash count http int

概述

分治FFT不是一个算法而是一种思想，一般指两种套路$CDQ$分治解决函数问题，分治+$FFT/NTT$合并背包

分治背包

问题

问题形如给出$n$种物品，第$i$种物品有$a_i$个，大小为$w_i$

答案的生成函数即为$\displaystyle{\prod_{i=1}^n(1+a_i x^{w_i})}$

解决方案也很简单，分治$Solve(l,mid),Solve(mid+1,r)$乘起来即可

复杂度$O(n\log^2 n)$

例题

CDQ分治+FFT

特殊化问题

$\mathtt{BSOJ5294}$:$\displaystyle{f(i)=\begin{cases}1&i=0\\\sum_{j=1}^if(i-j)g(j)&i\ne 0\end{cases}}$,其中$g$为给定数列,求$f(n)$

下面是$n=7$的一个举例

技术图片

首先这个卷积自己调用自己无法直接卷

考虑$CDQ$分治打包贡献

即对于$[l,r]$,首先计算$[l,mid]$并且算出从左到右的贡献

对于这道题，每到叶子结点，他的贡献就算完了

具体实现上有左闭右闭，左开右闭两种

这里用左开右闭,卡常版本

inline void CDQ(re int l,re int r,re int lg){
    if(l>=n||!lg)return ;re int i,mid=(l+r)>>1;
    CDQ(l,mid,lg-1);Getrev(1<<lg);
    memset(a+(r-l)/2,0,((r-l)/2)<<2);
    memcpy(a,f+l,((r-l)/2)<<2),memcpy(b,g,(r-l)<<2);
    NTT(a,1<<lg,1),NTT(b,1<<lg,1);for(i=0;i<r-l;++i)a[i]=1ll*a[i]*b[i]%mod;NTT(a,1<<lg,-1);
    for(i=(r-l)/2;i<r-l;i++)f[l+i]=Mod(f[l+i]+a[i]);
    CDQ(mid,r,lg-1);
}

一般化问题

考虑$[l,mid]$对$[mid+1,r]$的贡献无法及时算出情况

$\mathtt{BSOJ5295}$:$\displaystyle{g(i)=\begin{cases}?&i=1\\\sum_{j=1}^{i-1}f(i-j)f(j)&i\ne 1\end{cases}}$,其中$f(1)$给定,求$g(2)\cdots g(n)$

自己卷自己有什么区别呢

技术图片

那就是$[l,mid]$的$f$会卷上$[mid+1,r]$再贡献到$[mid+1,r]$上

考虑尽量算贡献,设$F_0(x)$为$[0,l)$这些内部贡献算完的部分,$F_1(x)则为$[l,r]$没算的部分

技术图片

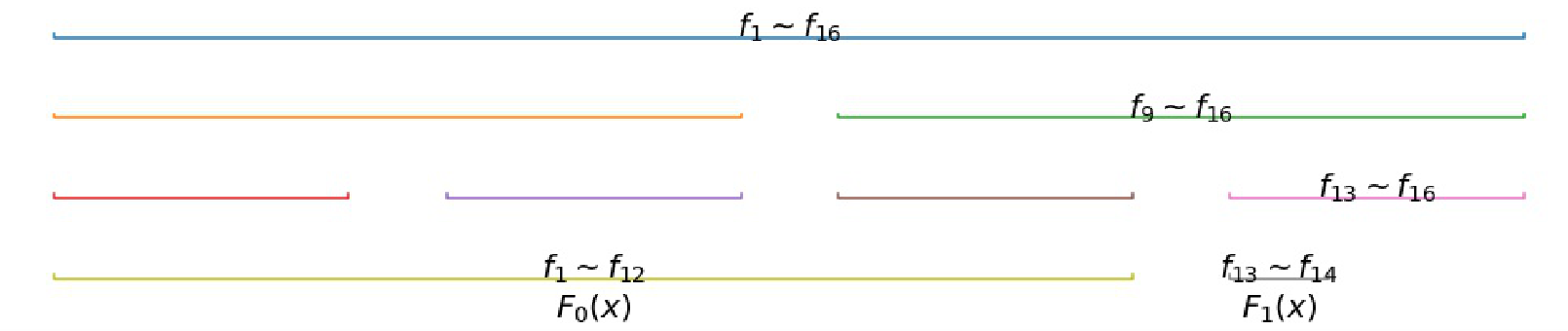
则$g=(F_0+F_1)^2=F_0^2+2F_0F_1+F_1^2$

考虑$F_0^2$前面已经被算过

我们要的项数是$[mid+1,r]$,考虑平移$F_1$,设平移$l$位后为$F_1'$

问题变为求$g'=2F_1'F_0$的$[mid+1-l,r-l]$位

和$g''=F_1'^2$的$[mid+1-2l,r-2l]$位(没有的舍掉即可)

inline void CDQ(re int l,re int r){
    if(l==r){if(l>1)f[l]=__builtin_popcount(g[l]);return ;}
    re int i,mid=(l+r)>>1,len;
    CDQ(l,mid);
    memcpy(a,f+l,(mid-l+1)<<2);memcpy(b,f,(std::min(r-l+1,l))<<2);
    len=Make(std::min(r-l+1,l),mid-l+1);
    NTT(a,len,1);NTT(b,len,1);
    memcpy(tmp,a,len<<2);for(i=0;i<len;++i)a[i]=1ll
    *a[i]*a[i]%mod;NTT(a,len,-1);
    for(i=0;i<len;++i)if(l*2+i<=r&&l*2+i>mid)g[l*2+i]=Mod(g[l*2+i]+a[i]);//F1^2(x)
    memcpy(a,tmp,len<<2);
    for(i=0;i<len;++i)a[i]=1ll*a[i]*b[i]%mod;NTT(a,len,-1);
    for(i=mid+1-l;i<=r-l;++i)g[l+i]=(g[l+i]+2ll*a[i])%mod;//F0(x)*F1(x)
    memset(a,0,len<<2),memset(b,0,len<<2);
    CDQ(mid+1,r);
}