标签:Once 讲解 分析 nbsp min order def 二叉树 clu
封装基于 BinaryTreeOperations 的 AVL 树(一种自平衡的二叉查找树)。
除了提供 BinaryTreeOperations 中的部分基础接口外,增加按键或节点指针的添加、删除操作。
在阅读本文前,您应该先了解 AVL 树中的旋转是怎么回事(相关文章很多且简单,笔者不再赘述)。
节点定义:
struct Node { _Ty key; int bf = 0; Node* left = nullptr; Node* right = nullptr; Node* parent = nullptr; Node(const _Ty& _key) :key(_key) {} };
AVL 树的规则:
任何节点的两个子树最大高度差为 1。
根据 AVL 树的规则,可见在插入和删除节点后,可能会打破 AVL 树的平衡,因此在插入和删除时应进行调整,使得 AVL 树能够自平衡。
因此在节点定义中加入平衡因子 bf 用于记录节点的平衡状态。
注:bf == 0 时,节点左右子树等高;bf == -1 时,左子树高一层;bf == 1 时,右子树高一层。bf 绝对值大于 1 时应该进行调整。
调整时需要进行旋转,旋转规则(令失衡节点为 cur):
① 左左_右旋:cur 左子树比右子树高两层(bf == -2)且 cur 的左子树 bf == -1 时:以 cur 右旋。
② 右右_左旋:cur 右子树比左子树高两层(bf == 2)且 cur 的左子树 bf == 1时:以 cur 左旋。
③ 左右_左右旋:cur 左子树比右子树高两层(bf == -2)且 cur 的左子树 bf == 1时:先以 cur 的左孩子左旋,再以 cur 右旋。
④ 右左_右左旋:cur 右子树比左子树高两层(bf == 2)且 cur 的左子树 bf == -1时:先以 cur 的右孩子右旋,再以 cur 左旋。
注意 bf 值的含义,左子树高还是右子树高或者等高。
单旋转方法已经在 BinaryTreeOperations.h 中给出。
现对旋转(单旋转和双旋转)后相关节点的平衡因子 bf 的变化进行说明(很多教程并未明确提出导致读者不能明确 bf 的变化)。
一、以左旋为例(单旋),右旋与左旋类似。
二、以 右左旋为例(双旋),左右旋与右左旋类似。
先看 一,与下图结合看(假设应该调整的节点是 X):
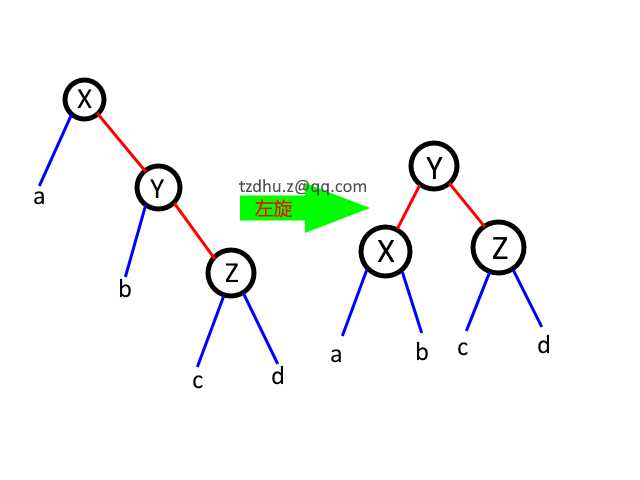
发现:
① Z 节点孩子未发生变动,因此 Z 节点的平衡因子不需要改变。
② 若 a 为空,则 b,c,d 必定为空(看 AVL 树的规则),因此,X,Y 的平衡因子均应该置零。(此时插入的节点为 Z)。
③ 若 a 不为空,则 b 一定不为空,c,d 一定其一为空,另一个不为空。(此时插入的节点为 c,d 之一,另一个为空)。可见,X,Y 节点任然平衡,平衡因子应置零。
再看 二,与下图结合看(假设应该调整的节点是 X):
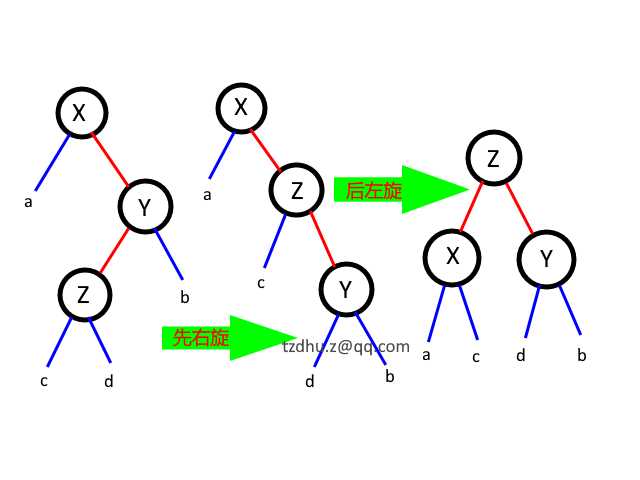
发现:
① Z 一定平衡(见下分析),其平衡因子 bf 应置零。
② 若 a 为空,则 b,c,d 必定为空(看 AVL 树的规则),X,Y,Z 的平衡因子均应该置零。(此时插入的节点为 Z)。
③ 若 a 不为空,则 b 一定不为空,c,d 一定其一为空,另一个不为空。(此时插入的节点为 c,d 之一,另一个为空)。
1)若插入为 c,则 X 平衡,其 bf 应置零,Y 右子树高,其 bf 应置 1。
2)若插入为 d,则 X 左子树高,其 bf 应置 -1,Y 平衡,其 bf 应置零。
至此,单旋双旋 旋转后旋转因子的变化说明清楚(调用 BinaryTreeOperations.h 中的旋转方法后应修改相关节点的 bf)。
插入操作:
可知,新插入的节点(令为 cur)必定是空位置,令插入后其父亲节点为 par(考虑成功插入的情况,只有成功插入才可能打破平衡)。
插入后的自平衡很简单,首先要知道,插入后 par 一定不会失去平衡(不用解释吧)。
插入后分为两种情况讨论即可(令 par 的父亲节点为 gpa,也就是新加节点的祖父节点):
一、par 有两个孩子。
二、par 只有一个孩子。
先看 一:par 有两个孩子,说明 cur 的插入没有给 par 或者 par 的祖先带来高度变化(没有新加层),此时直接返回即可。
再看二:par 只有一个孩子,说明 cur 的插入带来了高度变化,可能需要调整,此时应该怎能做呢?
① 先根据 par 和 gpa 的关系(即 par 是 gpa 的左孩子还是右孩子)来更新 gpa 的 bf。(默认插入时已经对 par 的平衡因子进行更新)
注:如何更新 par 和 gpa 的平衡因子不用说吧?(看是左孩子还是右孩子,右孩子 则 bf 自增,左孩子 则 bf 自减)。
② 根据 gpa 的平衡因子判断是否需要调整(即是否需要旋转)。
1)gpa 不需要旋转,则 par,gpa 分别指向各自父节点,继续 ① 操作,直到 2)或者 gpa 为空。
2)gpa 要旋转,则根据 par,gpa 的 bf 判断旋转方法进行调整,然后返回即可(请看上文 旋转规则)。
注:2)之后需要继续向上操作吗?(当然不需要!gpa 旋转后,对 gpa 的祖先而言没有高度的增加和减小)。
注意插入空树的情况。
至此,插入操作讲解完成,后序进行删除操作讲解,这会比插入操作稍加困难。
删除操作:
删除操作会比插入操作稍加复杂,下面先分析其原因所在(这里令 待删除节点为 cur,其父节点为 par)。
注:红黑树亦是如此,RBTree 的 删除比 AVLTree 的删除更加复杂,所以对于 AVLTree 的删除不用慌。
① 插入时, 新插入节点的 父亲节点 在插入前 一定:没有孩子 或 有一个孩子(该孩子一定没有孩子),而删除时 cur 可能没有孩子或有一个或两个孩子。
② 有无孩子都需要判断是否 cur 是根节点。
③ 应该如何删除 cur 且如何判断是否调整。
针对上述问题,我们可将其简化(假设删除 cur 时便对 par 的 bf 进行了刷新)。
① 删除节点是否为根节点的问题比较简单,只需做一下判断即可,后文不讨论该情况。
② 删除节点有两个孩子时:如二叉查找树一般,用后继节点代替并调用函数自身去删除后继结点(也可用前驱节点代替)。
③ 删除节点没有孩子。
④ 删除节点只有一个孩子。
注:② 中的后继结点(或前驱节点)一定属于 ③ 或 ④ 情况。
因此,将重点讨论 ② ③ 情况。
即:
一、删除节点没有孩子(是叶子节点)。
二、删除节点只有一个孩子。
注:令 cur 为待删除节点,par 为其父亲节点,gpa 为 par 的父亲节点。
先看 一(cur 是叶子节点):
① 若 cur 不存在兄弟节点,则删除 cur 会造成高度变化,gpa 是第一个可能失衡的节点(不用图也能想清楚吧)。
② 若 cur 存在兄弟节点,则 par 可能失衡(比如 par 右子树深度为2,左子树深度为一,删除左子树会失衡)。
OK,既然知道第一个可能失去平衡的节点,那只需要检测并调整就好了。
注意:什么情况需要继续向根节点回溯呢?即:通过旋转操作后 需要继续向上 还是。。。
当然是:par 经过旋转后才需要继续向上,若 par 不需要旋转,则 gpa 没有发生左右子树高度差变化,反之,par 经过旋转后 gpa 对应 par 子树的高度减小,则可能失衡。
所以 par 为经旋转是退出循环的条件。
继续回溯时,注意改变父节点的 bf。
再看 二(cur 只有一个孩子):
① cur 只有一个孩子,则该孩子一定没有孩子(否则 cur 不是平衡的)。
② 删除 cur,par 在 cur 的子树上高度一定减小,par 则有可能失衡,即 par 是第一个可能失衡点。
③ 删除 cur 时,用 cur 的孩子替代 cur 并删除 cur 的孩子,然后从 par 开始回溯判断是否需要调整,退出循环条件与前文一致。
至此,删除说明到此为止,AVL 树的说明也到此为止,最后给出示例代码。
测试代码 main.cpp:
#include <iostream> #include "AVLTree.h" using std::cout; using std::endl; int main() { AVLTree<int> avl; auto Add = [&avl](int _key) { cout << "Add " << _key << ":" << endl; avl.insert(_key); avl.levelTraversal(); cout << endl << "size: " << avl.size() << " level: " << avl.level() << endl << endl; }; auto il = { 3, 2, 6, 5, 8, 4, 9 }; for (auto& x : il) Add(x); auto Del = [&avl](int _key) { cout << "Del " << _key << ":" << endl; avl.erase(_key); avl.levelTraversal(); cout << endl << "size: " << avl.size() << " level: " << avl.level() << endl << endl; }; Del(2); Del(3); Del(8); return 0; }
头文件 AVLTree.h:
#pragma once #ifndef __AVLTREE_H__ #define __AVLTREE_H__ #include"BinaryTreeOperations.h" template<typename _Ty> class AVLTree { private: struct Node { _Ty key; int bf = 0; Node* left = nullptr; Node* right = nullptr; Node* parent = nullptr; Node(const _Ty& _key) :key(_key) {} }; public: AVLTree() = default; ~AVLTree() { BTO::clear(root); size_n = 0; } void clear() noexcept { BTO::clear(root); size_n = 0; } void preorderTraversal() { BTO::preorderTraversal(root, drawData); } void inorderTraversal() { BTO::inorderTraversal(root, drawData); } void postorderTraversal() { BTO::postorderTraversal(root, drawData); } void iterativePreorderTraversal() { BTO::iterativePreorderTraversal(root, drawData); } void iterativeInorderTraversal() { BTO::iterativeInorderTraversal(root, drawData); } void iterativePostorderTraversal() { BTO::iterativePostorderTraversal(root, drawData); } void levelTraversal() { BTO::levelTraversal(root, drawData); } Node* find(const _Ty& _key) { return BTO::find(root, _key); } Node* iterativeFind(const _Ty& _key) { return BTO::iterativeFind(root, _key); } Node* findMaximum() { return BTO::findMaximum(root); } Node* findMinimum() { return BTO::findMinimum(root); } size_t level() { return BTO::getLevel(root); } size_t size() const { return size_n; } void insert(const _Ty&); bool erase(const _Ty&); void erase(Node*); private: void LL_R(Node*); void RR_L(Node*); void LR_LR(Node*); void RL_RL(Node*); static void drawData(const Node* _node) { std::cout << _node->key << " "; } private: size_t size_n = 0; Node* root = nullptr; }; template<typename _Ty> void AVLTree<_Ty>::LL_R(Node* _node) { _node = BTO::rightRotate(_node); _node->bf = _node->right->bf = 0; if (_node->parent == nullptr) root = _node; } template<typename _Ty> void AVLTree<_Ty>::RR_L(Node* _node) { _node = BTO::leftRotate(_node); _node->bf = _node->left->bf = 0; if (_node->parent == nullptr) root = _node; } template<typename _Ty> void AVLTree<_Ty>::LR_LR(Node* _node) { BTO::leftRotate(_node->left); _node = BTO::rightRotate(_node); if (_node->right->right == nullptr) _node->left->bf = _node->right->bf = 0; else { if (_node->right->left == nullptr) { _node->right->bf = 1; _node->left->bf = 0; } else { _node->left->bf = 0; _node->right->bf = -1; } } _node->bf = 0; if (_node->parent == nullptr) root = _node; } template<typename _Ty> void AVLTree<_Ty>::RL_RL(Node* _node) { BTO::rightRotate(_node->right); _node = BTO::leftRotate(_node); if (_node->left->left == nullptr) _node->left->bf = _node->right->bf = 0; else { if (_node->left->right == nullptr) { _node->left->bf = -1; _node->right->bf = 0; } else { _node->left->bf = 0; _node->right->bf = 1; } } _node->bf = 0; if (_node->parent == nullptr) root = _node; } template<typename _Ty> void AVLTree<_Ty>::insert(const _Ty& _key) { auto ret = BTO::insert(root, _key); if (ret.second) ++size_n; else return; auto temp = ret.first; if (temp->parent == nullptr) return; if (temp == temp->parent->left) temp->parent->bf += -1; else temp->parent->bf += 1; temp = temp->parent; if (temp->left != nullptr && temp->right != nullptr) return; Node* pa = temp->parent; while (pa != nullptr) { if (temp == pa->left) pa->bf += -1; else pa->bf += 1; if (pa->bf == -2) { if (temp->bf == -1) LL_R(pa); else LR_LR(pa); break; } else if (pa->bf == 2) { if (temp->bf == -1) RL_RL(pa); else RR_L(pa); break; } temp = pa; pa = pa->parent; } } template<typename _Ty> bool AVLTree<_Ty>::erase(const _Ty& _key) { bool succeed = false; Node* del = BTO::find(root, _key); if (del != nullptr) { erase(del); succeed = true; } return succeed; } template<typename _Ty> void AVLTree<_Ty>::erase(Node* _node) { if (_node == nullptr) return; --size_n; Node* pa = nullptr; Node* temp = nullptr; if (_node->left == nullptr && _node->right == nullptr) { if (_node == root) { root = nullptr; delete _node; return; } if (_node == _node->parent->left) { _node->parent->left = nullptr; _node->parent->bf += 1; temp = _node->parent->right; } else { _node->parent->right = nullptr; _node->parent->bf += -1; temp = _node->parent->left; } pa = _node->parent; delete _node; } else if (!(_node->left != nullptr && _node->right != nullptr)) { if (_node->parent == nullptr) { if (_node->left != nullptr) root = _node->left; else root = _node->right; root->parent = nullptr; delete _node; return; } if (_node == _node->parent->left) { _node->parent->left = _node->left == nullptr ? _node->right : _node->left; if (_node->left != nullptr) _node->left->parent = _node->parent; else _node->right->parent = _node->parent; _node->parent->bf += 1; temp = _node->parent->right; } else { _node->parent->right = _node->left == nullptr ? _node->right : _node->left; if (_node->left != nullptr) _node->left->parent = _node->parent; else _node->right->parent = _node->parent; _node->parent->bf += -1; temp = _node->parent->left; } pa = _node->parent; delete _node; } else { Node* de = BTO::findMinimum(_node->right); _node->key = de->key; ++size_n; erase(de); } if (pa != nullptr && pa->bf == 0) { temp = pa; pa = pa->parent; if (pa != nullptr) { if (temp == pa->left) { temp = pa->right; pa->bf += 1; } else { temp = pa->left; pa->bf += -1; } } } while (pa != nullptr) { if (pa->bf == -2) { if (temp->bf == -1 || temp->bf == 0) LL_R(pa); else LR_LR(pa); } else if (pa->bf == 2) { if (temp->bf == -1) RL_RL(pa); else RR_L(pa); } else break; bool isLeft = temp == pa->left ? 1 : 0; pa = temp->parent; if (pa != nullptr) { if (isLeft) { temp = pa->left; pa->bf += -1; } else { temp = pa->right; pa->bf += 1; } } } } #endif // !__AVLTREE_H__
标签:Once 讲解 分析 nbsp min order def 二叉树 clu
原文地址:https://www.cnblogs.com/teternity/p/AVLTree.html