为什么逻辑回归损失函数不用均方损失/二元逻辑回归的损失函数适合采用对数损失函数

标签：为什么   因此   width   梯度下降法   height   sof   多个   解决   预测   

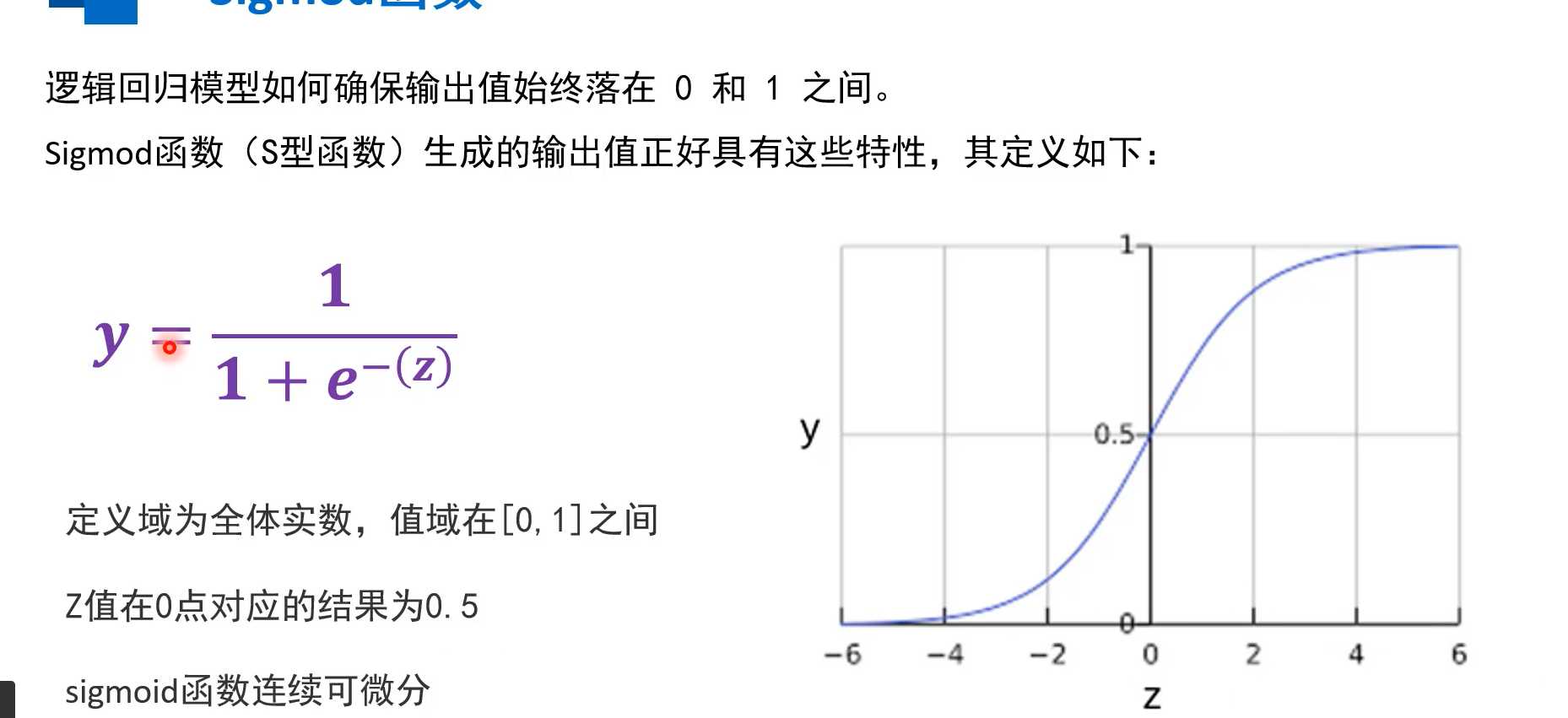
逻辑回归可以用于处理二元分类问题，将输出值控制在[0，1]区间内，为确保输出值时钟若在0到1之间，采用sigmoid函数，其具有该特性，将线性回归训练得到的模型输出数据作z = x1*w1+x2*w2+...+xn*wn+b代入得到y,保证了y在0~1之间

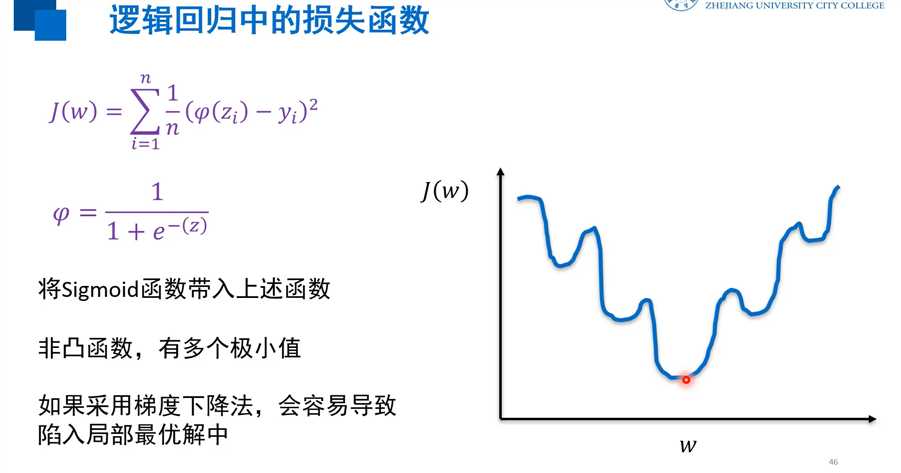
逻辑回归中用到sigmoid函数，若用均方误差则为非凸函数，有多个极小值，采用梯度下降法容易现如局部最优解中

因此在二元逻辑回归的损失函数一般采用对数损失函数

y‘是x代入得到的预测值，介于0~1之间的；

若标签值为1，我们希望预测的结果也是越接近1越好，越接近说明损失越小 =》》后项1 - y为 0 直接消掉，则-y log(y‘)中y‘越接近1，则式子越接近0 ，损失和越小

同理，若标签值为0，则前项消掉，后项-log(1 - y‘)预测值越接近0，式子越小

softmax可以解决多元分类问题

为什么逻辑回归损失函数不用均方损失/二元逻辑回归的损失函数适合采用对数损失函数

标签：为什么   因此   width   梯度下降法   height   sof   多个   解决   预测   

原文地址：https://www.cnblogs.com/Theo-sblogs/p/12291527.html