在线|二轮辅导[06][三角函数+解三角形02]

标签：download   uri   思路   软件下载   变形   png   使用   百度网   适应   

视频地址

百度云盘地址：待上传

使用方法：下载观看，能保证高清清晰度，针对百度网盘限速，请使用PanDownload软件下载，该软件的下载地址：https://www.lanzous.com/i8ua9na；

思维导图

• 三角函数+解三角形思维导图；

典例剖析

例1求值\(\cfrac{1+cos20^{\circ}}{2sin20^{\circ}}-sin10^{\circ}(\cfrac{1}{tan5^{\circ}}-tan5^{\circ})\)

分析：原式\(=\cfrac{2cos^210^{\circ}}{2\cdot 2sin10^{\circ}cos10^{\circ}}-sin10^{\circ}(\cfrac{cos5^{\circ}}{sin5^{\circ}}-\cfrac{sin5^{\circ}}{cos5^{\circ}})\)

\(=\cfrac{cos10^{\circ}}{2sin10^{\circ}}-sin10^{\circ}(\cfrac{cos^25^{\circ}-sin^25^{\circ}}{sin5^{\circ}cos5^{\circ}})\)

\(=\cfrac{cos10^{\circ}}{2sin10^{\circ}}-sin10^{\circ}\cfrac{2cos10^{\circ}}{2sin5^{\circ}cos5^{\circ}})\)

\(=\cfrac{cos10^{\circ}}{2sin10^{\circ}}-2cos10^{\circ}\)

\(==\cfrac{cos10^{\circ}}{2sin10^{\circ}}-\cfrac{2cos10^{\circ}\cdot 2sin10^{\circ}}{2sin10^{\circ}}\)

\(=\cfrac{cos10^{\circ}-2sin20^{\circ}}{2sin10^{\circ}}\)

\(=\cfrac{cos10^{\circ}-2sin(30^{\circ}-10^{\circ})}{2sin10^{\circ}}\)

\(=\cfrac{cos10^{\circ}-cos10^{\circ}+2\cdot \cfrac{\sqrt{3}}{2}sin10^{\circ}}{2sin10^{\circ}}\)

\(=\cfrac{\sqrt{3}}{2}\)。

例2求值\(\cfrac{cos10^{\circ}-\sqrt{3}cos(-100^{\circ})}{\sqrt{1-sin10^{\circ}}}\)

分析：原式\(=\cfrac{cos10^{\circ}-\sqrt{3}cos(100^{\circ})}{\sqrt{1-sin10^{\circ}}}\)

\(=\cfrac{cos10^{\circ}+\sqrt{3}sin10^{\circ}}{\sqrt{1-sin10^{\circ}}}\)

\(=\cfrac{cos10^{\circ}+\sqrt{3}sin10^{\circ}}{\sqrt{(cos5^{\circ}-sin5^{\circ})^2}}\)

\(=\cfrac{cos10^{\circ}+\sqrt{3}sin10^{\circ}}{(cos5^{\circ}-sin5^{\circ})^2}\)

\(=\cfrac{2sin(10^{\circ}+30^{\circ})}{-\sqrt{2}sin(5^{\circ}-45^{\circ})}\)

\(=\cfrac{2sin40^{\circ}}{\sqrt{2}sin40^{\circ}}=\sqrt{2}\)。

例3化简求值\(\cfrac{cos40^{\circ}}{cos25^{\circ}\cdot \sqrt{1-sin40^{\circ}}}\)

分析：原式\(=\cfrac{cos40^{\circ}}{cos25^{\circ}\cdot \sqrt{(sin20^{\circ}-cos20^{\circ})^2}}\)

\(=\cfrac{cos40^{\circ}}{cos25^{\circ}\cdot |sin20^{\circ}-cos20^{\circ}|}\)

\(=\cfrac{cos^220^{\circ}-sin^220^{\circ}}{cos25^{\circ}(cos20^{\circ}-sin20^{\circ})}\)

\(=\cfrac{cos20^{\circ}+sin20^{\circ}}{cos25^{\circ}}\)

\(=\cfrac{\sqrt{2}sin(20^{\circ}+45^{\circ})}{cos25^{\circ}}\)

\(=\cfrac{\sqrt{2}sin65^{\circ}}{cos25^{\circ}}=\sqrt{2}\).

例4化简求值\(\cfrac{\sqrt{3}tan12^{\circ}-3}{(4cos^212^{\circ}-2)sin12^{\circ}}\)

分析：原式=\(\cfrac{\sqrt{3}\cfrac{sin12^{\circ}}{cos12^{\circ}}-3\cfrac{cos12^{\circ}}{cos12^{\circ}}}{2(2cos^212^{\circ}-1)sin12^{\circ}}\)

\(=\cfrac{\sqrt{3}\cdot \cfrac{sin12^{\circ}-\sqrt{3}cos12^{\circ}}{cos12^{\circ}}}{2cos24^{\circ}sin12^{\circ}}\)

\(=\cfrac{\sqrt{3}\cdot 2sin(12^{\circ}-60^{\circ})}{2cos24^{\circ}sin12^{\circ}cos12^{\circ}}\)

\(=\cfrac{2\sqrt{3}sin(-48^{\circ})}{sin24^{\circ}cos24^{\circ}}=-4\sqrt{3}\)。

练-1化简求值\(\cfrac{\sqrt{3}-tan12^{\circ}}{(2cos^212^{\circ}-1)sin12^{\circ}}=8\)

练-2化简求值\(sin50^{\circ}(1+\sqrt{3}tan10^{\circ})=1\)

例5函数\(f(x)=2cos(\omega x+\phi)(\omega\neq 0)\)对任意\(x\)都有\(f(\cfrac{\pi}{4}+x)=f(\cfrac{\pi}{4}-x)\)成立，则\(f(\cfrac{\pi}{4})\)的值为【】

分析：由任意\(x\)都有\(f(\cfrac{\pi}{4}+x)=f(\cfrac{\pi}{4}-x)\)成立，可知\(x=\cfrac{\pi}{4}\)为函数的一条对称轴，

而正弦型或余弦型函数在对称轴处必然会取到最值，故\(f(\cfrac{\pi}{4})=\pm 2\)，选B。

解后反思：此题目如果不注意函数的性质，往往会想到求\(\omega\)和\(\phi\)，这样思路就跑偏了。

例6【2018云南玉溪一模】函数\(f(x)=\sqrt{3}sin2x+2cos^2x\)的一条对称轴为直线【】

分析：\(f(x)=2sin(2x+\cfrac{\pi}{6})+1\)，

法1：比较繁琐，令\(2x+\cfrac{\pi}{6}=k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，则\(x=\cfrac{k\pi}{2}+\cfrac{\pi}{6}\)，\(k\in Z\)，即对称轴有无数条，

令\(k=0\)，得到其中的一条对称轴为\(x=\cfrac{\pi}{6}\)，当\(k\)取其他的值时，都不能得到其他的选项，故选\(B\)。

法2：比较简单，利用函数在对称轴处的函数值能取到最值，故只需验证即可，

比如，将\(x=\cfrac{\pi}{12}\)代入\(sin(2x+\cfrac{\pi}{6})\)，即\(sin\cfrac{\pi}{3}\)，并不能使得其取到最值\(\pm 1\)，故舍去\(A\)；

将\(x=\cfrac{\pi}{6}\)代入\(sin(2x+\cfrac{\pi}{6})\)，即\(sin\cfrac{\pi}{2}\)，能使得其取到最值\(+1\)，故\(B\)必然满足；用同样的方法可以验证其余的选项错误；

例7【2018江西赣州5月适应性考试】若函数\(f(x)=3cos(2x+\cfrac{\pi}{6})-a\)在\([0，\cfrac{\pi}{2}]\)上有两个零点\(x_1\)，\(x_2\)，则\(x_1+x_2\)=【】

分析：只需要考虑函数\(y=cos(2x+\cfrac{\pi}{6})\)的对称性即可，由\(2x+\cfrac{\pi}{6}=k\pi\)，\(k\in Z\)，

得到对称轴\(x=\cfrac{k\pi}{2}-\cfrac{\pi}{12}\)，由题可知，对称轴必须在\([0，\cfrac{\pi}{2}]\)内，令\(k=1\)，得到对称轴为\(x=\cfrac{5}{12}\)，

又两个零点\(x_1\)和\(x_2\)关于对称轴\(x=\cfrac{5}{12}\)对称，故\(x_1+x_2=\cfrac{5}{6}\)。

例8【2019届高三理科数学三轮模拟试题】若函数\(f(x)=asinx+cosx\)(\(a\)为常数，\(a\in R\))的图像关于直线\(x=\cfrac{\pi}{6}\)对称，则函数\(g(x)=sinx+acosx\)的图像【】

分析：\(y=f(x)=\sqrt{a^2+1}sin(x+\phi)\)，其中\(tan\phi=\cfrac{1}{a}\)，

由函数\(f(x)=asinx+cosx\)的图像关于直线\(x=\cfrac{\pi}{6}\)对称，可知\(\phi=\cfrac{\pi}{3}\)，

则\(a=\cfrac{\sqrt{3}}{3}\)，又\(g(x)=sinx+\cfrac{\sqrt{3}}{3}cosx=\cfrac{2\sqrt{3}}{3}sin(x+\cfrac{\pi}{6})\)，

逐项验证，可知选\(D\)。

例9【2018广东茂名一模】【有图情形】已知函数\(f(x)＝Asin(\omega x+\phi)(A＞0，\omega> 0，0＜\phi＜\pi)\)，其导函数的图象\(f'(x)\)如图所示，则\(f(\cfrac{\pi}{2})\)＝【】

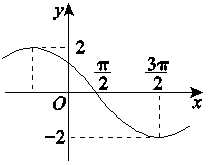
分析：由于\(f'(x)=\omega Acos(\omega x+\phi)\)，由\(\cfrac{T}{4}=\cfrac{3\pi}{2}-\cfrac{\pi}{2}=\pi\)，故\(T=4\pi\)，故\(\omega=\cfrac{2\pi}{4\pi}=\cfrac{1}{2}\)，

又由图可知，\(\omega A=\cfrac{1}{2}A=2\)，故\(A=4\)，又由图\(f'(\cfrac{\pi}{2})=0=2cos(\cfrac{1}{2}\times \cfrac{\pi}{2}+\phi)\)，即\(\cfrac{\pi}{4}+\phi=k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，故\(\phi=k\pi+\cfrac{\pi}{4}\)，令\(k=0\)，即\(\phi=\cfrac{\pi}{4}\in (0,\pi)\)，

故函数\(f(x)=4sin(\cfrac{1}{2}x+\cfrac{\pi}{4})\)，则\(f(\cfrac{\pi}{2})=4\)，故选\(D\)。

例10【2019高三理科数学二轮资料用题】【有图情形】已知函数\(f(x)＝Atan(\omega x＋\phi)\)，其中\(\omega ＞0\)，\(|\phi|＜\cfrac{\pi}{2}\)，\(y＝f(x)\)的部分图象如图，则\(f(\cfrac{\pi}{24})\)＝__________.

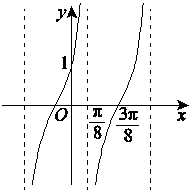
分析：由图可知，\(\cfrac{T}{2}=\cfrac{3\pi}{8}-\cfrac{\pi}{8}=\cfrac{\pi}{4}\)，则\(T=\cfrac{\pi}{2}\)，故\(\omega=\cfrac{\pi}{T}=2\)，

又当\(x=\cfrac{3\pi}{8}\)时，\(2\times \cfrac{3\pi}{8}+\phi=k\pi\)，\(k\in Z\)，则\(\phi=k\pi-\cfrac{3\pi}{4}\)，

令\(k=1\)，则\(\phi=\pi-\cfrac{3\pi}{4}=\cfrac{\pi}{4}\in (-\cfrac{\pi}{2}，\cfrac{\pi}{2})\)，又\(x=0\)时，\(y=1\)，

即\(Atan(2\times 0+\cfrac{\pi}{4})=1\)，故\(A=1\)，即\(f(x)=tan(2x+\cfrac{\pi}{4})\)，

故\(f(\cfrac{\pi}{24})=tan(2\times \cfrac{\pi}{24}+\cfrac{\pi}{4})=\sqrt{3}\)。

例11【无图情形】【2018届湖南衡阳八中第二次月考】已知函数\(y＝sin(ωx＋φ)\) \((ω>0，0<φ<π)\)的最小正周期为\(π\)，且函数图象关于点\((-\cfrac{3\pi}{8}，0)\)对称，则该函数的解析式为________．

分析：由于函数\(y＝sin(ωx＋φ)\)的最小正周期为\(π\)，故\(\omega=2\)，又图象关于点\((-\cfrac{3\pi}{8}，0)\)对称，

则\(2\times (-\cfrac{3\pi}{8})+\phi=k\pi\)，故\(\phi=k\pi+\cfrac{3\pi}{4}\)，\(k\in Z\) ,

当\(k=0\)时，\(\phi=\cfrac{3\pi}{4}\in (0,\pi)\)，故解析式为\(y=sin(2x+\cfrac{3\pi}{4})\).

例12【三轮模拟考试理科用题】已知\(\alpha\)为第二象限角，\(sin(\alpha+\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{10}\)，则\(tan\cfrac{\alpha}{2}\)的值为多少？

法1：变形得到\(\cfrac{\sqrt{2}}{2}(sin\alpha+cos\alpha)=\cfrac{\sqrt{2}}{10}\)，

解得\(sin\alpha+cos\alpha=\cfrac{1}{5}\)，又因为\(\alpha\)为第二象限角，

再结合勾股数可得\(sin\alpha=\cfrac{4}{5}，cos\alpha=-\cfrac{3}{5}\)；

故\(tan\alpha=-\cfrac{4}{3}\)，又由八卦图法可知\(\cfrac{\alpha}{2}\)在第一、三象限，

故\(tan\cfrac{\alpha}{2}>0\)，再由\(tan\alpha=-\cfrac{4}{3}=\cfrac{2tan\cfrac{\alpha}{2}}{1-(tan\cfrac{\alpha}{2})^2}\)，

解方程得到\(tan\cfrac{\alpha}{2}=2\)；

法2：同上法，得到\(sin\alpha=\cfrac{4}{5}，cos\alpha=-\cfrac{3}{5}\)；

\(tan\cfrac{\alpha}{2}=\cfrac{sin\cfrac{\alpha}{2}}{cos\cfrac{\alpha}{2}}\)

\(=\cfrac{2sin\cfrac{\alpha}{2}cos\cfrac{\alpha}{2}}{2cos\cfrac{\alpha}{2}cos\cfrac{\alpha}{2}}\)

\(=\cfrac{sin\alpha}{1+cos\alpha}=\cfrac{\cfrac{4}{5}}{1-\cfrac{3}{5}}=2\)；

例13(三轮模拟考试理科用题)已知\(f(x)=2Acos^2(\omega x+\phi)(A>0,\omega>0,0<\phi<\cfrac{\pi}{2})\)，直线\(x=\cfrac{\pi}{3}\)和点\((\cfrac{\pi}{12},0)\)分别是函数\(f(x)\)图象上相邻的一条对称轴和一个对称中心，则函数\(f(x)\)的单调增区间为（ ）.

分析：这类题目一般需要先将\(f(x)\)转化为正弦型或者余弦型，再利用给定的条件分别求\(\omega\)和\(\phi\)，由

\(f(x)=2Acos^2(\omega x+\phi)=A[cos2(\omega x+\phi)+1]-A=Acos(2\omega x+2\phi)\)，

故其周期为\(T=\cfrac{2\pi}{2\omega}=\cfrac{\pi}{\omega}\)，

又由题目可知\(\cfrac{T}{4}=\cfrac{\pi}{3}-\cfrac{\pi}{12}=\cfrac{\pi}{4}\)，则\(T=\pi=\cfrac{\pi}{\omega}\)，

故\(\omega=1\)，则函数简化为\(f(x)=Acos(2x+2\phi)\)，再利用直线\(x=\cfrac{\pi}{3}\)是函数\(f(x)\)图象上的一条对称轴，

故\(2\times \cfrac{\pi}{3}+2\phi=k\pi,(k\in Z)\),解得\(\phi=\cfrac{k\pi}{2}-\cfrac{\pi}{3}\)，

令\(k=1\)，则\(\phi=\cfrac{\pi}{6}\in (0,\cfrac{\pi}{2})\)，满足题意，故\(f(x)=Acos(2x+2\phi)=Acos(2x+\cfrac{\pi}{3})\).

令\(2k\pi-\pi\leq 2x+\cfrac{\pi}{3}\leq 2k\pi(k\in Z)\)，解得\(k\pi-\cfrac{2\pi}{3}\leq x \leq k\pi-\cfrac{\pi}{6}\)，即单调递增区间为\(A．[k\pi-\cfrac{2\pi}{3} ，k\pi-\cfrac{\pi}{6}](k\in Z)\);

例14【2014\(\cdot\)新课标全国卷Ⅰ】设\(\alpha，\beta \in (0，\cfrac{\pi}{2})\)，且\(tan\alpha=\cfrac{1+sin\beta}{cos\beta}\)，则【】

分析：切化弦得到，\(\cfrac{sin\alpha}{cos\alpha}=\cfrac{1+sin\beta}{cos\beta}\)，

即\(sin\alpha cos\beta-cos\alpha sin\beta=cos\alpha\)，即\(sin(\alpha-\beta)=cos\alpha\)；

又由已知可得，\(-\cfrac{\pi}{2}<\alpha-\beta<-\cfrac{\pi}{2}\)，

再结合\(sin(\alpha-\beta)=cos\alpha\)，\(\alpha \in (0，\cfrac{\pi}{2})\)，\(cos\alpha>0\)，

故可将\(-\cfrac{\pi}{2}<\alpha-\beta<-\cfrac{\pi}{2}\)压缩为\(0<\alpha-\beta<-\cfrac{\pi}{2}\)，，

这样\(sin(\alpha-\beta)=cos\alpha\)；且\(\alpha，\alpha-\beta \in (0，\cfrac{\pi}{2})\)，

故有\((\alpha-\beta)+\alpha=\cfrac{\pi}{2}\)，即\(2\alpha-\beta=\cfrac{\pi}{2}\)，选C.

例15【2016\(\cdot\)上海卷】【解三角方程】方程\(3sinx=1+cos2x\)在区间\([0，2\pi]\)上的解为_______________。

分析：采用升幂降角公式，得到\(3sinx=1+1-2sin^2x\)，

整理为\(2sin^2x+3sinx-2=0\)，即\((sinx+2)(2sinx-1)=0\)

解得\(sinx=-2(舍去)\)或\(sinx=\cfrac{1}{2}\)，

再由\(sinx=\cfrac{1}{2}\)，\(x\in[0，2\pi]\)，

采用图像可得，\(x=\cfrac{\pi}{6}\)或\(x=\cfrac{5\pi}{6}\)。

例16【连比形式，巧设比例因子】在\(\Delta ABC\)中，\(tanA:tanB:tanC=1:2:3\)，求\(\cfrac{AC}{AB}\)的值；

分析：(巧设比例因子)设\(tanA=k,tanB=2k,tanC=3k,(k>0)\),

则由\(tanA\times tanB\times tanC=tanA+tanB+tanC\)可知，\(6k=6k^3\),解得\(k=1\).则有\(tanA=1,tanB=2,tanC=3\),

再设比例因子，比如设\(sinB=2m,cosB=m,(m>0)\),由平方关系可得，\(5m^2=1,m=\cfrac{1}{\sqrt{5}}\),

故\(sinB=\cfrac{2}{\sqrt{5}},sinC=\cfrac{3}{\sqrt{10}}\),则\(\cfrac{AC}{AB}=\cfrac{sinB}{sinC}=\cfrac{\cfrac{2}{\sqrt{5}}}{\cfrac{3}{\sqrt{10}}}=\cfrac{2\sqrt{2}}{3}\).

例17已知\(tan\alpha=\cfrac{1}{2}\)，求\(sin^4\alpha-cos^4\alpha\)的值。

【法1】：方程组法，由\(\left\{\begin{array}{l}{\cfrac{sin\alpha}{cos\alpha}=\cfrac{1}{2}}\\{sin^2\alpha+cos^2\alpha=1}\end{array}\right.\)，

解得\(sin^2\alpha=\cfrac{1}{5}\)，\(cos^2\alpha=\cfrac{4}{5}\)，

代入得到\(sin^4\alpha-cos^4\alpha=-\cfrac{3}{5}\)；

【法2】：齐次式法，\(sin^4\alpha-cos^4\alpha=(sin^2\alpha-cos^2\alpha)(sin^2\alpha+cos^2\alpha)=sin^2\alpha-cos^2\alpha\)

\(=-cos2\alpha=-\cfrac{cos^2\alpha-sin^2\alpha}{sin^2\alpha+cos^2\alpha}=\cfrac{1-tan^2\alpha}{1+tan^2\alpha}=-\cfrac{3}{5}\)；

【法3】：由\(\cfrac{sin\alpha}{cos\alpha}=\cfrac{1}{2}\)，引入比例因子，可设\(sin\alpha=k\)，\(cos\alpha=2k(k\neq 0)\)，

由\(k^2+(2k)^2=1\)，可得\(k^2=\cfrac{1}{5}\)，故\(k^4=\cfrac{1}{25}\)，

则\(sin^4\alpha-cos^4\alpha=k^4-(2k)^4=-15k^4=-\cfrac{3}{5}\)；

例18求值：\(sin^21^{\circ}+sin^22^{\circ}+sin^23^{\circ}+\cdots+sin^288^{\circ}+sin^289^{\circ}=\)

分析：\(sin^21^{\circ}+sin^289^{\circ}=1\)，\(sin^22^{\circ}+sin^288^{\circ}=1\)，\(\cdots\)，\(sin^244^{\circ}+sin^246^{\circ}=1\)，\(sin^245^{\circ}=\cfrac{1}{2}\)，

故原式=\(44+\cfrac{1}{2}=44.5\)。

在线|二轮辅导[06][三角函数+解三角形02]

标签：download   uri   思路   软件下载   变形   png   使用   百度网   适应   

原文地址：https://www.cnblogs.com/wanghai0666/p/12289956.html