标签：class   com   ast   include   github   不用   struct   node   seq   

codeforces 1272 F. Two Bracket Sequences（三维dp + bfs）

题目大意

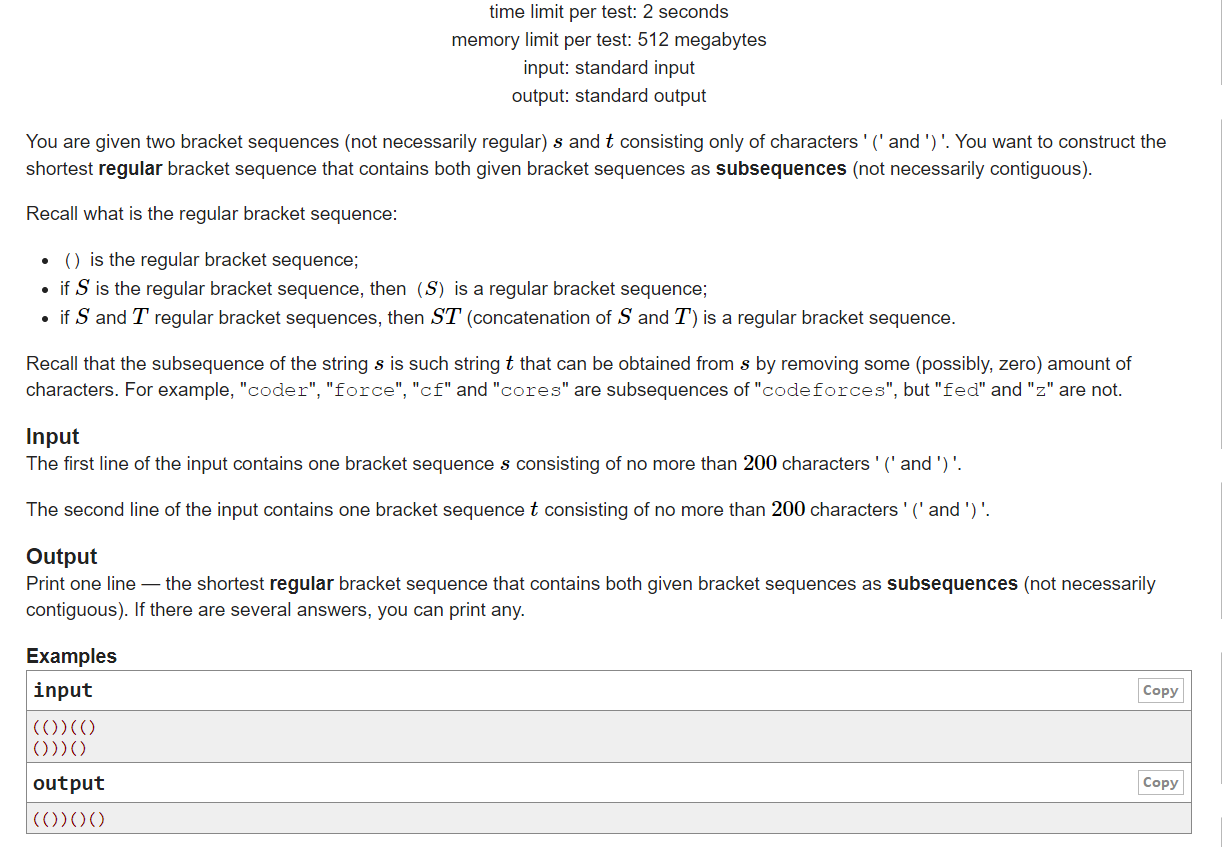
输入两个括号序列 s,t（不一定合法），你需要构造一个尽可能短的合法括号序列使得s,t 都是这个序列的子序列（子序列意味着不用连续）

解题思路

dp[i][j][k]表示匹配到s的第i个字符，匹配到t的第j个字符，并且此时(的个数比)多k个的时候的最小合法序列长度，k的上限是200（s和t中最多200个（或者)）。

状态转移：

枚举答案合法序列的每一位是放置(或者)

? 放置(，如果s[i]==‘(‘ -> ni=i+1,t[j]==‘(‘ -> nj=j+1, dp[ni][nj][z+1]=dp[i][j][z]+1

? 放置)，如果s[i]==‘)‘ -> ni=i+1,t[j]==‘)‘ -> nj=j+1, dp[ni][nj][z-1]=dp[i][j][z]+1

整个过程需要满足0<=z<=200 下界是因为z<0时左括号个数小于右括号个数将无法形成合法序列。每一个步转移需要记录父节点坐标和父节点通过什么字符转移到当前状态，最终状态为dp[s.size()][t.size()][0]，从这个状态沿着父节点回退到dp[0][0][0]。

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int maxn=210;
const int inf=0x3f3f3f3f;
int dp[maxn][maxn][maxn];
struct node{int x,y,z;char c;}st[maxn][maxn][maxn];
string s,t;
int sz,tz;
int nx,ny,nz;
inline void bfs(){
    sz=s.size(),tz=t.size();
    memset(dp,0x3f,sizeof dp);
    dp[0][0][0]=0;
    queue<node> q;q.push(node{0,0,0});
    while(!q.empty()){
        node tp=q.front();q.pop();
        //'('
        nx=tp.x+(tp.x<sz&&s[tp.x]=='(');
        ny=tp.y+(tp.y<tz&&t[tp.y]=='(');
        nz=tp.z+1;
        if(nz<=200&&dp[nx][ny][nz]==inf){
            dp[nx][ny][nz]=dp[tp.x][tp.y][tp.z]+1;
            q.push(node{nx,ny,nz});
            st[nx][ny][nz]=node{tp.x,tp.y,tp.z,'('};

        }
        
        //)
        nx=tp.x+(tp.x<sz&&s[tp.x]==')');
        ny=tp.y+(tp.y<tz&&t[tp.y]==')');
        nz=tp.z-1;
        if(nz>=0&&dp[nx][ny][nz]==inf){
            dp[nx][ny][nz]=dp[tp.x][tp.y][tp.z]+1;
            q.push(node{nx,ny,nz});
            st[nx][ny][nz]=node{tp.x,tp.y,tp.z,')'};
        }
    }
}

int main(){
    cin>>s>>t;
    bfs();

    string res="";
    int x=sz,y=tz,z=0;

    int px,py,pz;
    while(x||y||z){
        res+=st[x][y][z].c;
        px=st[x][y][z].x;
        py=st[x][y][z].y;
        pz=st[x][y][z].z;
        x=px,y=py,z=pz;
    }

    sz=res.size();
    for(int i=sz-1;i>=0;--i)cout<<res[i];
    cout<<endl;
    return 0;
}

# codeforces 1272 F. Two Bracket Sequences（三维dp + bfs）

标签：class   com   ast   include   github   不用   struct   node   seq   

原文地址：https://www.cnblogs.com/sstealer/p/12300988.html