lingo解决整数线性规划（小题）

标签：组成   span   ebe   覆盖   决策   整数   代码   for   model   

------------恢复内容开始------------

　　小编最近在看解决整数线性规划。

　　对于一维的决策变量，使用matlab和lingo均可。

　　matlab可以用intlinprog(f,incont,a,b,aeq,beq,ln.hn)

　　f对应的所求式子的列向量，incont对应着 为整数的相关索引，a为不等式的限定矩阵，b为不等式的资源矩向量，同理aeqhebeq为等式的对应矩阵和向量。

　　下面用lingo求解整数线性规划问题：

　　两种方法：

　　第一种，按照每个备选校址，写出对应的覆盖小区的向量，组成一个矩阵。

　　列向量分别代表每一个校址对应所覆盖的小区，分别为0，1（二进制变量）

model:
sets:
col/1..6/:x;
row/1..8/;
link(row,col):a;
endsets
data:
a = 1 1 1 0 0 0
    0 1 0 1 0 0
    0 0 1 0 1 0
    0 0 0 1 0 1
    1 1 1 0 0 0
    0 0 0 0 1 1
    1 0 0 0 0 0 
    0 1 0 1 0 1;
enddata
min = @ sum(col(i):x(i));
@for(row(i):@sum(col(j):a(i,j)*x(j))>1);
@for(col(j):@bin(x(j)));
end

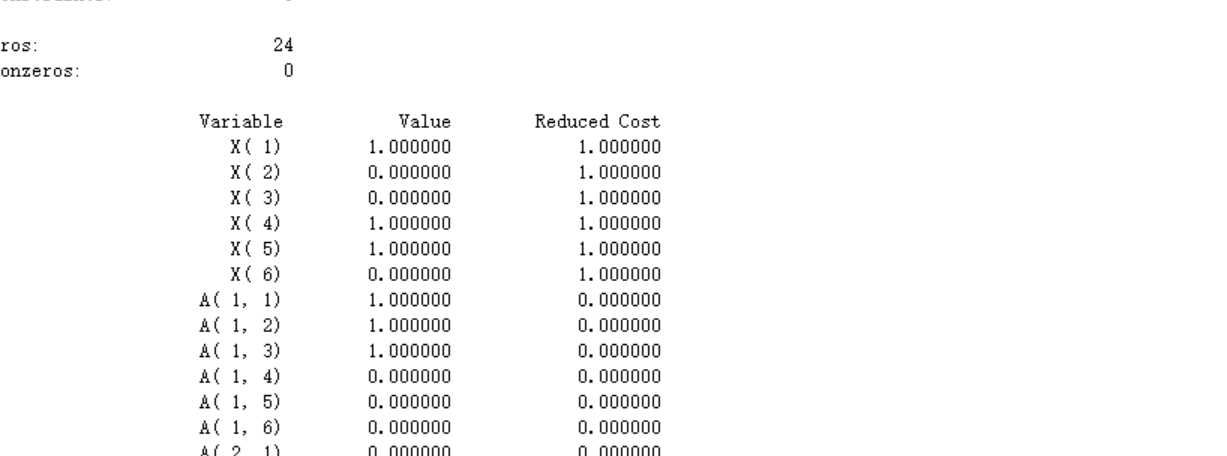
如图所示，显示答案为1，4，5.

　　第二种方法：

　　xi{1： 在备选校址Bi建学校， 0： 在备选校址Bi不建学校}

　　由于小区A1可以被备选校址B1，B2，B3所间的学校所覆盖，所以有约束条件：

　　x1 + x2 + x3 >=1

　　类似的其他的也一样：

         min  求和（xi）（小编求和符号复制不过来）

　　s.t:

　　　　x1 + x2 + x3 >=1

　　　　x2 + x4 >=1

　　　　x3 + x5 >=1

　　　　x4 + x6 >=1

　　　　x5 + x6 >=1

　　　　x1 >=1

　　　　x1 + x4 + x6 >=1

　　lingo程序如下：

　　代码更加简洁

model：
sets:
var/1..6/:x;
endsets
min=@sum(var:x);
x(1)+x(2)+x(3)>1
x(2)+x(4)>1
x(3)+x(5)>1
x(4)+x(6)>1
x(1)>1
x(2)+x(4)+x(6)>1
end

------------恢复内容结束------------

lingo解决整数线性规划（小题）

标签：组成   span   ebe   覆盖   决策   整数   代码   for   model   

原文地址：https://www.cnblogs.com/a-runner/p/12301021.html