标签:input min 输入输出 assert bit 通过 oat isp rap
如题,给出一个 NNN 次函数,保证在范围 [l,r][l, r][l,r] 内存在一点 xxx,使得 [l,x][l, x][l,x] 上单调增,[x,r][x, r][x,r] 上单调减。试求出 xxx 的值。
第一行一次包含一个正整数 NNN 和两个实数 l,rl, rl,r,含义如题目描述所示。
第二行包含 N+1N + 1N+1 个实数,从高到低依次表示该 NNN 次函数各项的系数。
输出为一行,包含一个实数,即为 xxx 的值。四舍五入保留 555 位小数。
3 -0.9981 0.5 1 -3 -3 1
-0.41421
对于 100%100\%100% 的数据,7≤N≤137 \le N \le 137≤N≤13。
【样例解释】
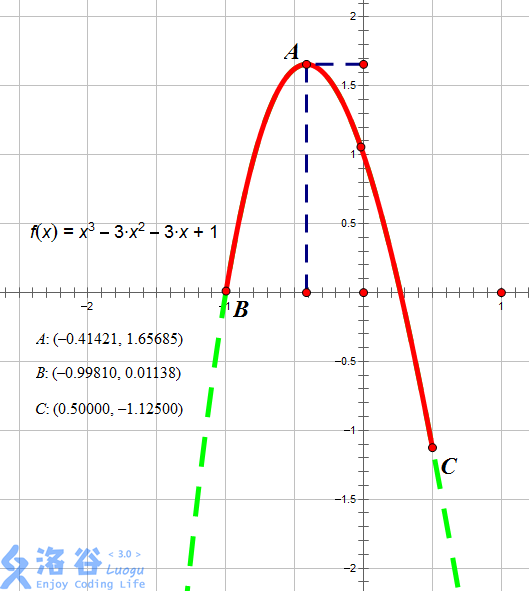
如图所示,红色段即为该函数 f(x)=x3−3x2−3x+1f(x) = x^3 - 3 x^2 - 3x + 1f(x)=x3−3x2−3x+1 在区间 [−0.9981,0.5][-0.9981, 0.5][−0.9981,0.5] 上的图像。
当 x=−0.41421x = -0.41421x=−0.41421 时图像位于最高点,故此时函数在 [l,x][l, x][l,x] 上单调增,[x,r][x, r][x,r] 上单调减,故 x=−0.41421x = -0.41421x=−0.41421,输出 −0.41421-0.41421−0.41421。
(Tip.l&r的范围并不是非常大ww不会超过一位数)
思路:
求单峰极值可以想到模拟退火三分,和二分类比一下,二分需要一个中间点,三分需要两个中间点,就是三等分点然后根据求的是极大值还是极小值比较三分点并转移
CODE

1 #include <bits/stdc++.h> 2 #define dbg(x) cout << #x << "=" << x << endl 3 #define eps 1e-8 4 5 using namespace std; 6 typedef long long LL; 7 8 template<class T>inline void read(T &res) 9 { 10 char c;T flag=1; 11 while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;res=c-‘0‘; 12 while((c=getchar())>=‘0‘&&c<=‘9‘)res=res*10+c-‘0‘;res*=flag; 13 } 14 15 namespace _buff { 16 const size_t BUFF = 1 << 19; 17 char ibuf[BUFF], *ib = ibuf, *ie = ibuf; 18 char getc() { 19 if (ib == ie) { 20 ib = ibuf; 21 ie = ibuf + fread(ibuf, 1, BUFF, stdin); 22 } 23 return ib == ie ? -1 : *ib++; 24 } 25 } 26 27 int qread() { 28 using namespace _buff; 29 int ret = 0; 30 bool pos = true; 31 char c = getc(); 32 for (; (c < ‘0‘ || c > ‘9‘) && c != ‘-‘; c = getc()) { 33 assert(~c); 34 } 35 if (c == ‘-‘) { 36 pos = false; 37 c = getc(); 38 } 39 for (; c >= ‘0‘ && c <= ‘9‘; c = getc()) { 40 ret = (ret << 3) + (ret << 1) + (c ^ 48); 41 } 42 return pos ? ret : -ret; 43 } 44 45 int n; 46 double l,r; 47 double a[20]; 48 49 double f(double x) {///多项式求值秦九韶算法把2n+1次乘法n次加法简化为n次乘法和n次加法 50 double u = 1, p = 0; 51 for(int i = n; i >= 0; --i) { 52 p += u*a[i]; 53 u *= x; 54 } 55 return p; 56 } 57 58 double ts(double l, double r) { 59 while(l + eps < r) { 60 double lmid = l + (r-l)/3, rmid = r - (r-l)/3; 61 if(f(lmid) <= f(rmid)) { 62 l = lmid; 63 } 64 else { 65 r = rmid; 66 } 67 } 68 return r; 69 } 70 71 int main() 72 { 73 memset(a, 0, sizeof(a)); 74 scanf("%d",&n); 75 scanf("%lf%lf",&l, &r); 76 77 for(int i = 0; i <= n; ++i) { 78 scanf("%lf", &a[i]); 79 } 80 printf("%.5f\n",ts(l,r)); 81 return 0; 82 }
标签:input min 输入输出 assert bit 通过 oat isp rap
原文地址:https://www.cnblogs.com/orangeko/p/12305905.html