标签:online math 相交关系 推理 关系 证明 inf code 技术
我是谁? 鸽子王。
\(T1:\)
不会
\(T2:\)
不会
\(T3:\)
首先联想到这道题:bzoj2965保护古迹
想到能不能转成对偶图跑最小割
然后发现并不能做。。。
但根据这个想到:对偶图的最小割\(<=>\)平面图的最短路
(以下坐标均指代交点)
继续推理容易发现只有一个关键点的时候,显然不会跨过(1,1)到关键点左上角的最短路
而当有多个关键点时一定不会跨过这些(1,1)到这些关键点的左上角的最短路树。
证明:
如图,因为画的路径是一个环,考虑环和树的相交关系
由于树的根位于环上,假设环与树还有其他交点,则存在两个交点
那么对于交点间的路径,一定是沿着树走更优
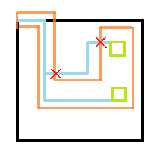
所以我们现在要求的便是不跨越最短路树的最小的从(1,1)开始的环
那么如何控制某些边不被跨越?
我们可以将每个交点拆成4个点

在可以跨越边两侧的点之间连边
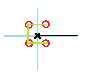
再将关键点覆盖的点删去

然后从(1,1)拆出的点跑最短路即可
复杂度\(O(n^2log^2n)\)
标签:online math 相交关系 推理 关系 证明 inf code 技术
原文地址:https://www.cnblogs.com/Gkeng/p/12307572.html