标签:force ++ ret main 黄色 http nbsp cos nan
题目: 传送门
题意:
定义Nanosoft的 logo 为 四个大小相同的正方形合并成一个大正方形。左上角是红色的,右上角是绿色的,左下角是黄色的,右下角是蓝色的。
例如以下这些都是
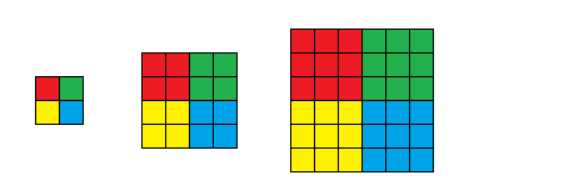
以下这些都不是
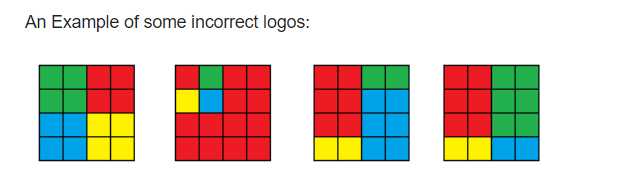
给你一个n * m的矩阵,这个矩阵由 4 个大写字母 “R” , "G", “Y”, “B” 构成,这四个大写字母分别代表红色,绿色,黄色,蓝色。
有Q次询问,每次询问, 输入两个坐标,(x1, y1), (x2, y2) 代表 以 (x1, y1) 为矩阵左上角的坐标,(x2, y2)为矩阵右下角的坐标的矩阵中,能作为Nanosoft的 logo的 子矩阵面积最大是多少。
题解:
首先,定义 pre[ i ][ j ][ col ] 代表矩阵 (1, 1) , (i, j) 中 颜色为 col 的格有多少个, 也就是二维前缀和, 这个可以很简单预处理出来。
显然, 能作为Nanosoft的 logo 的都必须是正方形, 且边长必须是偶数。
然后定义 dp[ i ][ j ][ k ] 为 以(i, j) 为右下角, 边长为 k 的正方形中, 能作为Nanosoft的logo的子正方形的边长的最大值, 也就是以 (i - k + 1, j - k + 1) 为左上角, (i, j)为右下角的正方形中,能作为Nanosoft的 logo的子正方形边长的最大值。
转移方程就是: dp[ i ][ j ][ k ] = max({ dp[ i ][ j ][ k ], dp[ i ][ j ][k - 1], dp[i - 1][ j ][k - 1], dp[ i ][j - 1][k - 1], dp[i - 1][j - 1][k - 1] });
我们还可以在o(1)的时间里判断 以 (i,j)为右下角坐标,边长为 k 的正方形是否能整个作为Nanosoft的 logo,能的话,那dp[ i ][ j ][ k ] 就是 k 了。
然后对于每个询问, 我们知道, 最大的正方形的边长就是 min(x2 - x1 + 1, y2 - y1 + 1);
那我们可以枚举这样的正方形。 最多每次询问都枚举 max(n, m) 次, 那复杂度就是 n * q 不至于超时。

#include <bits/stdc++.h> #define LL long long #define mem(i, j) memset(i, j, sizeof(i)) #define rep(i, j, k) for(int i = j; i <= k; i++) #define dep(i, j, k) for(int i = k; i >= j; i--) #define pb push_back #define make make_pair #define INF INT_MAX #define inf LLONG_MAX #define PI acos(-1) using namespace std; const int N = 510; char a[N][N]; char s[] = "RGYB"; int n, m, q; int pre[N][N][4]; ///第三维,0代表红色,1代表绿色,2代表黄色,3代表蓝色 int dp[N][N][N]; int check(int lux, int luy, int rdx, int rdy, int col) { return pre[rdx][rdy][col] - pre[rdx][luy - 1][col] - pre[lux - 1][rdy][col] + pre[lux - 1][luy - 1][col]; } void init() { rep(k, 0, 3) rep(i, 1, n) rep(j, 1, m) pre[i][j][k] = pre[i - 1][j][k] + pre[i][j - 1][k] - pre[i - 1][j - 1][k] + (a[i][j] == s[k]); rep(i, 1, n) rep(j, 1, m) { for(int k = 1; k <= min(i, j); k++) { if(k % 2 == 0) { int len = k / 2; if(check(i - len + 1, j - len + 1, i, j, 3) == len * len &&check(i - len + 1, j - k + 1, i, j - len, 2) == len * len &&check(i - k + 1, j - len + 1, i - len, j, 1) == len * len &&check(i - k + 1, j - k + 1, i - len, j - len, 0) == len * len) dp[i][j][k] = k; } dp[i][j][k] = max({ dp[i][j][k], dp[i][j][k - 1], dp[i - 1][j][k - 1], dp[i][j - 1][k - 1], dp[i - 1][j - 1][k - 1] }); } } } int main() { scanf("%d %d %d", &n, &m, &q); rep(i, 1, n) scanf("%s", a[i] + 1); init(); while(q--) { int x1, x2, y1, y2; scanf("%d %d %d %d", &x1, &y1, &x2, &y2); int len = min(x2 - x1 + 1, y2 - y1 + 1); int ans = 0; if(x2 - x1 > y2 - y1) { int dis = (x2 - x1) - (y2 - y1); rep(i, 0, dis) ans = max(ans, dp[x2 - i][y2][len]); } else { int dis = (y2 - y1) - (x2 - x1); rep(i, 0, dis) ans = max(ans, dp[x2][y2 - i][len]); } printf("%d\n", ans * ans); } return 0; }
标签:force ++ ret main 黄色 http nbsp cos nan
原文地址:https://www.cnblogs.com/Willems/p/12307668.html