标签:现在 turn 四种 void 均值 swa 子串 lld 图片
A. Three Strings【思维】

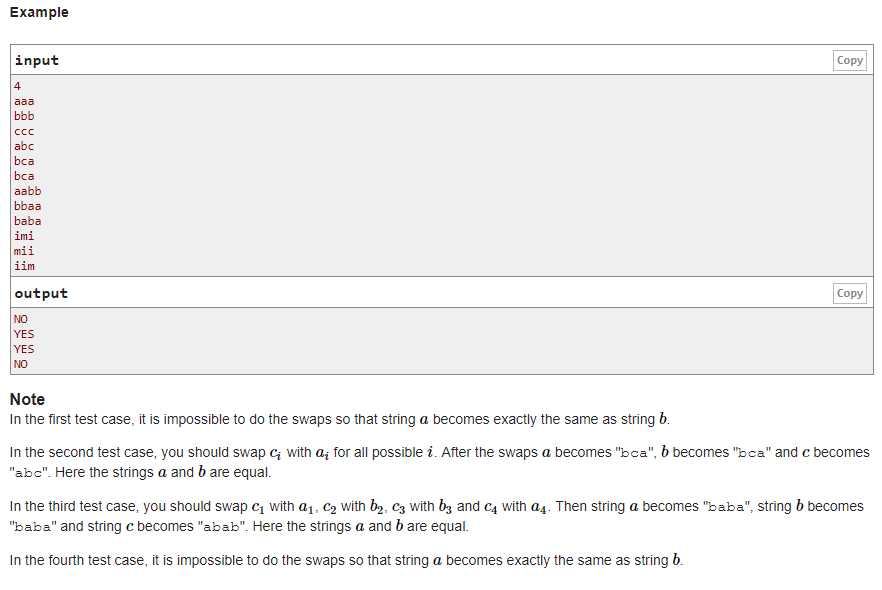
题意:给你三个串a,b,c,对于串的每一个字符i,必须进行以下操作:swap(a_i,c_i)或者swap(b_i,c_i),问是否存在操作方案使得操作完之后使得ab串相等
题解:判断是否存在a_i,b_i同时不等于c_i的情况
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int T=0; char a[101],b[101],c[101]; int main() { scanf("%d",&T); while(T--) { scanf("%s%s%s",a,b,c); int l=strlen(a),fl=0; for(int i=0;i<l;i++) { if(a[i]!=c[i] && b[i]!=c[i]){fl=1;break;} } printf(fl?"NO\n":"YES\n"); } return 0; }
B. Motarack‘s Birthday【思维】

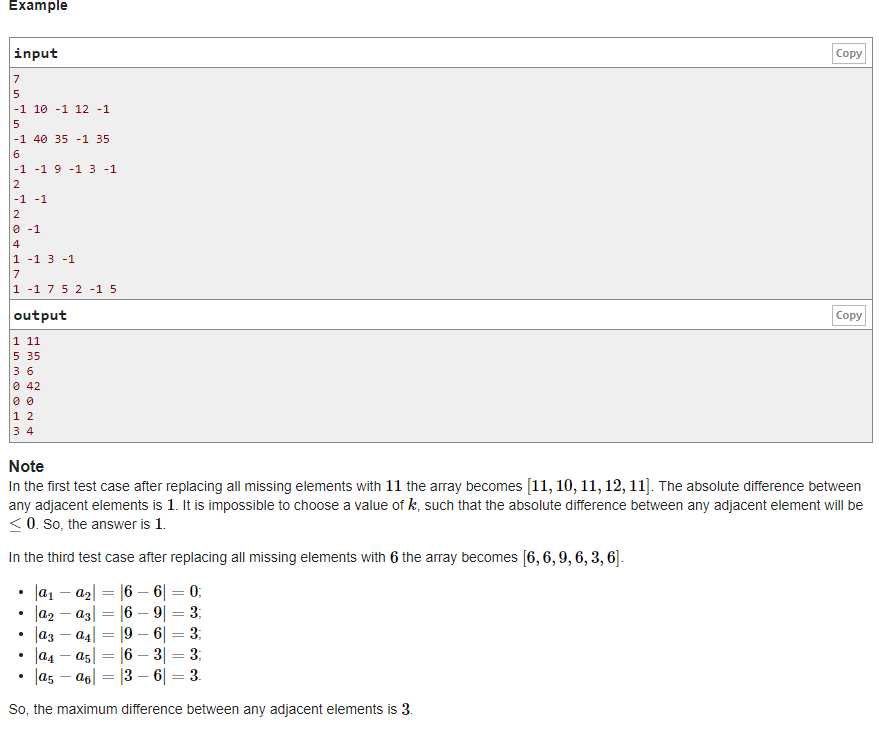
题意:确定一个k,将k替换所有的-1,使得max(ai-ai-1)最大
题解:只要找到贴着-1的最大值和最小值,求其平均值即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long #define INF 1000000001 using namespace std; int T,n; ll a[100001],b[100001],m,mn=INF,mx=-INF,k; ll Abs(ll x){if(x<0)return -x;else return x;} bool check() { ll mx=-INF,mn=INF,t2=-INF; for(int i=2;i<=n;i++) { if(a[i-1]==-1) { if(a[i]!=-1) { mx=max(mx,a[i]); mn=min(mn,a[i]); } } else { if(a[i]==-1) { mx=max(mx,a[i-1]); mn=min(mn,a[i-1]); } else t2=max(t2,Abs(a[i]-a[i-1])); } } if(mx==-INF)mx=mn=0; m=(mx+mn)/2; t2=max(t2,max(mx-m,m-mn)); k=t2; } int main() { scanf("%d",&T); while(T--) { scanf("%d",&n);m=0; for(int i=1;i<=n;i++)scanf("%lld",&a[i]); check(); printf("%lld %lld\n",k,m); } return 0; }
C. Ayoub‘s function【思维+贪心】
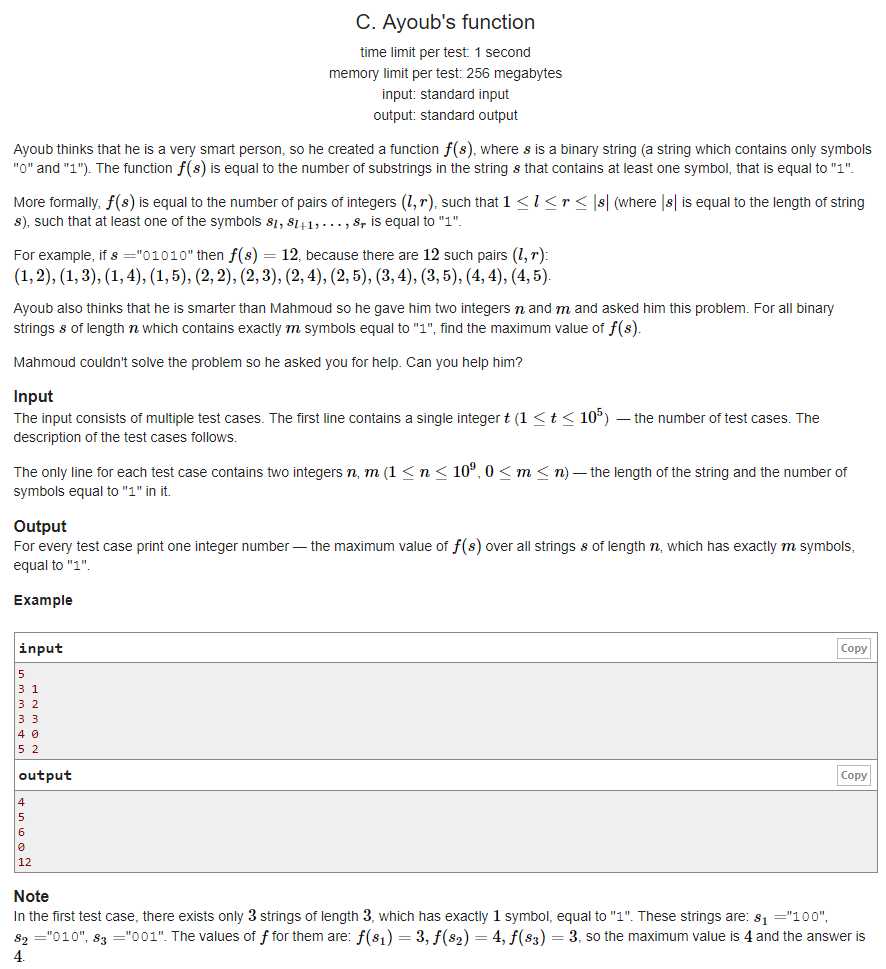
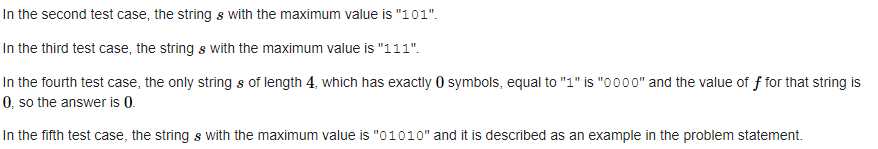
题意:长度n的01串中有m个1,一个合法子串当且仅当子串里存在至少一个1,让你求出所有满足这样条件的01串中的合法子串最多有多少
题解:考虑逆向思维,合法最多等同于不合法最少,一个子串不合法当且仅当只有0,
设一个长度为l的不合法子串,显然其对答案的贡献是l*(l+1)/2
m个1将长度为n的串分成了m+1个子串,这些子串的长度和为n-m
现在问题转化为求sigma(li*(li+1))/2)最小
注意到如果长度l变为长度l+1,那么一定存在另一个长度l变为l-1,
l->l+1会对答案增加贡献l+1,而l->l-1会对答案减少贡献l-1
因为l+1>l-1,所以让所有都尽可能小,因此n-m个0平均分配给m+1个串可以得到最优解
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int T; ll n,m; int main() { scanf("%d",&T); while(T--) { scanf("%lld%lld",&n,&m); ll l=(n-m)/(m+1); ll res=(n-m)-l*(m+1); ll a=res,b=m+1-res; ll suma=(l+2)*(l+1)/2*a,sumb=(l+1)*l/2*b; ll ans=(n+1)*n/2-suma-sumb; printf("%lld\n",ans); } return 0; }
D. Time to Run【模拟+构造】
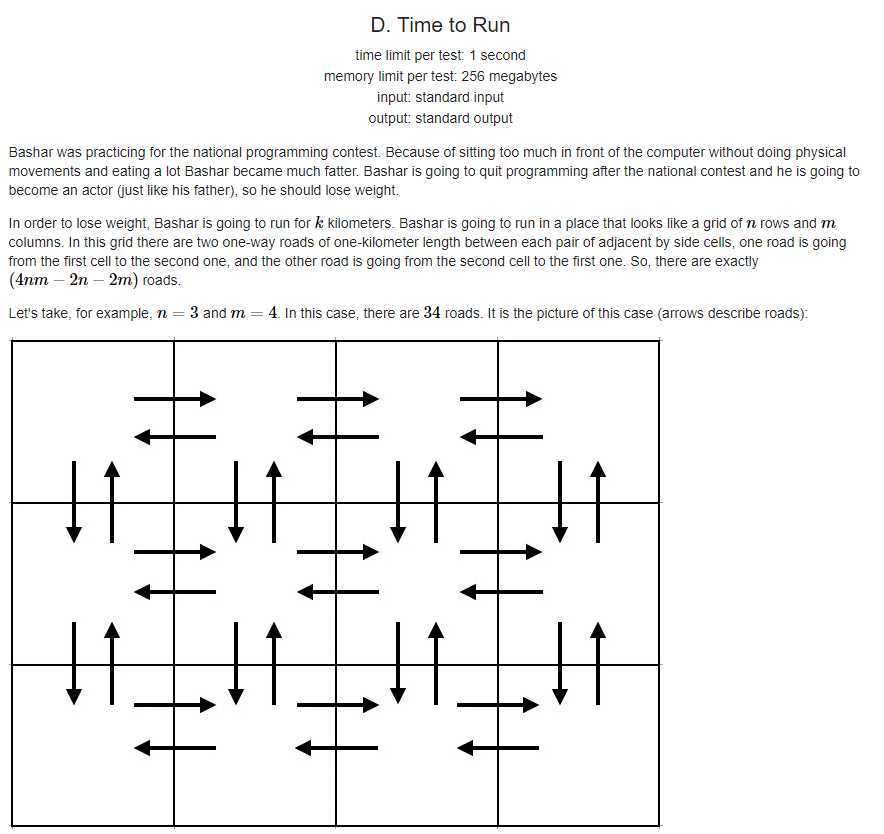


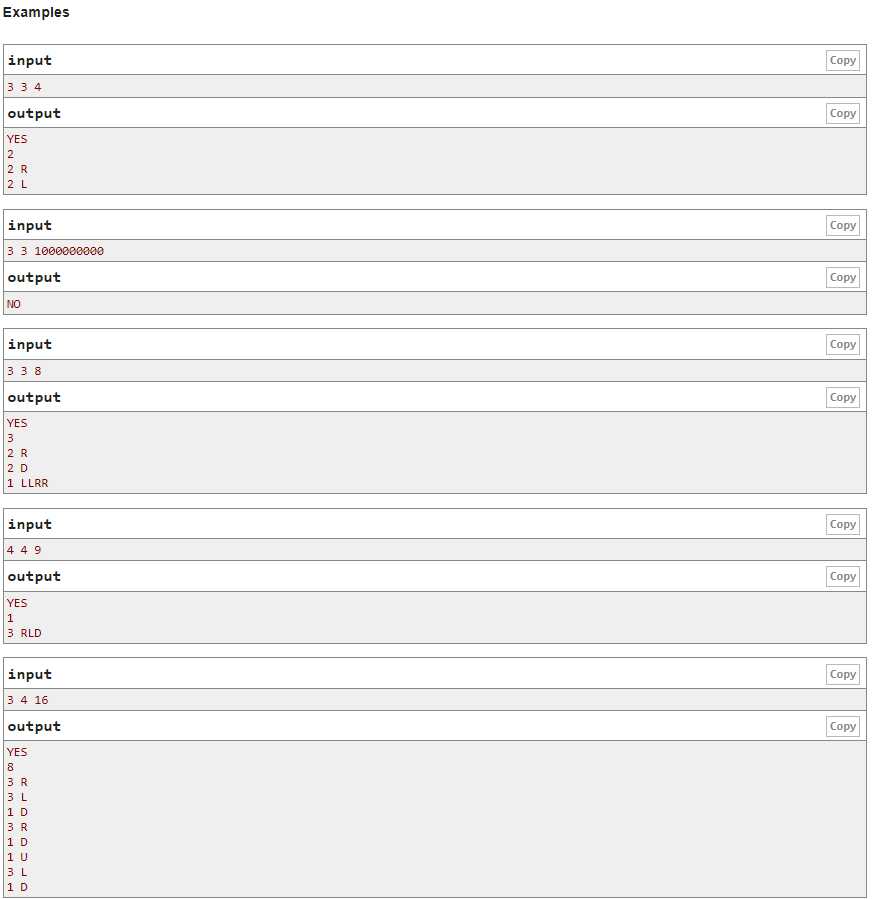
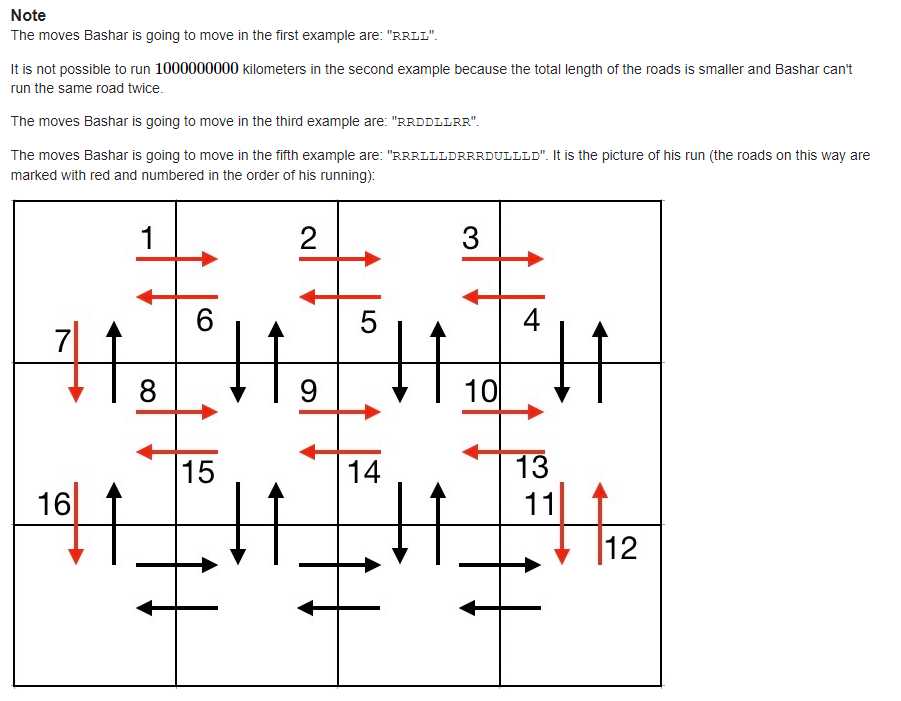
题意:给定n*m的地图,每两个相邻的格子有一个双向边,每条边只能走一遍,求一个路径使得长度为k
题解:模拟构造一个一笔画即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int n,m,k; struct node { int t; char ch[10]; }st[3001]; int stn; void add(int mod,int t) { stn++; if(mod==1) { st[stn].t=t; st[stn].ch[0]=‘R‘; st[stn].ch[1]=‘D‘; st[stn].ch[2]=‘U‘; } if(mod==11) { st[stn].t=t; st[stn].ch[0]=‘R‘; } if(mod==12) { st[stn].t=t; st[stn].ch[0]=‘D‘; } if(mod==13) { st[stn].t=t; st[stn].ch[0]=‘U‘; } if(mod==2) { st[stn].t=t; st[stn].ch[0]=‘L‘; } } int main() { scanf("%d%d%d",&n,&m,&k); if(4*n*m-2*n-2*m<k)return !printf("NO\n"); printf("YES\n"); int t=0,x=1,y=1; while(k>0) { if(x<n) { if(m>1) { if(3*(m-1)<k) { k-=3*(m-1); add(1,m-1); } else { if(k/3>0)add(1,k/3); k-=k/3*3; if(k>0)k--,add(11,1); if(k>0)k--,add(12,1); if(k>0)k--,add(13,1); break; } if(m-1<k) { k-=(m-1); add(2,m-1); } else { add(2,k); k=0; break; } } if(k>0) { add(12,1); k--; } x++; } else { if(m>1) { if((m-1)<k) { k-=(m-1); add(11,m-1); } else { add(11,k); k=0; break; } if((m-1)<k) { k-=(m-1); add(2,m-1); } else { add(2,k); k=0; break; } } add(13,k); k=0; break; } } printf("%d\n",stn); for(int i=1;i<=stn;i++)printf("%d %s\n",st[i].t,st[i].ch); return 0; }
E. Nanosoft【二维ST表】
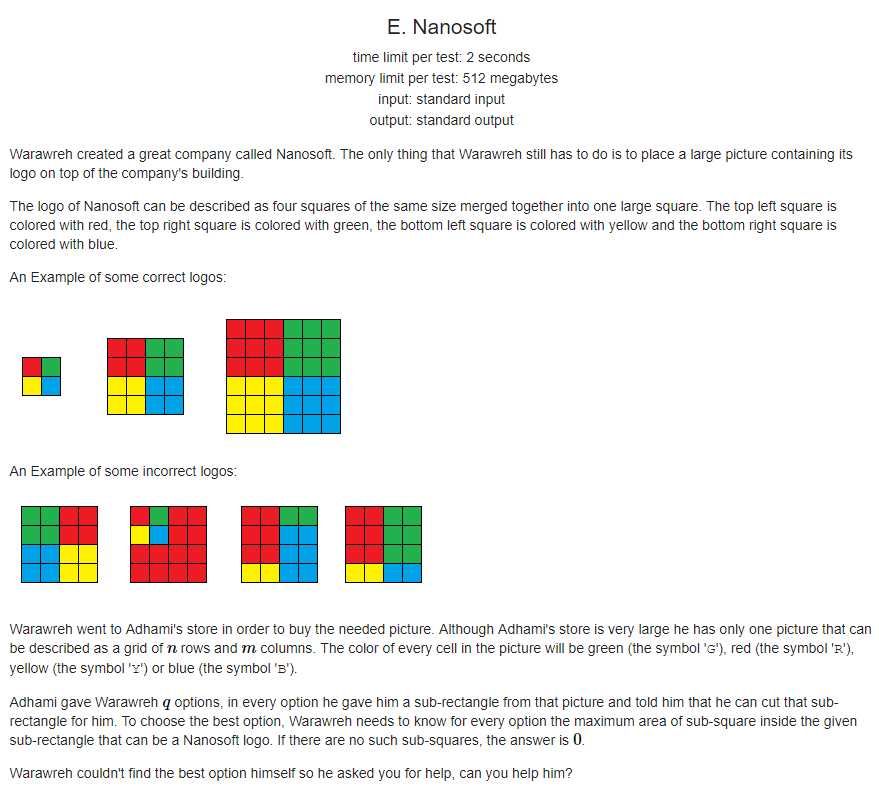
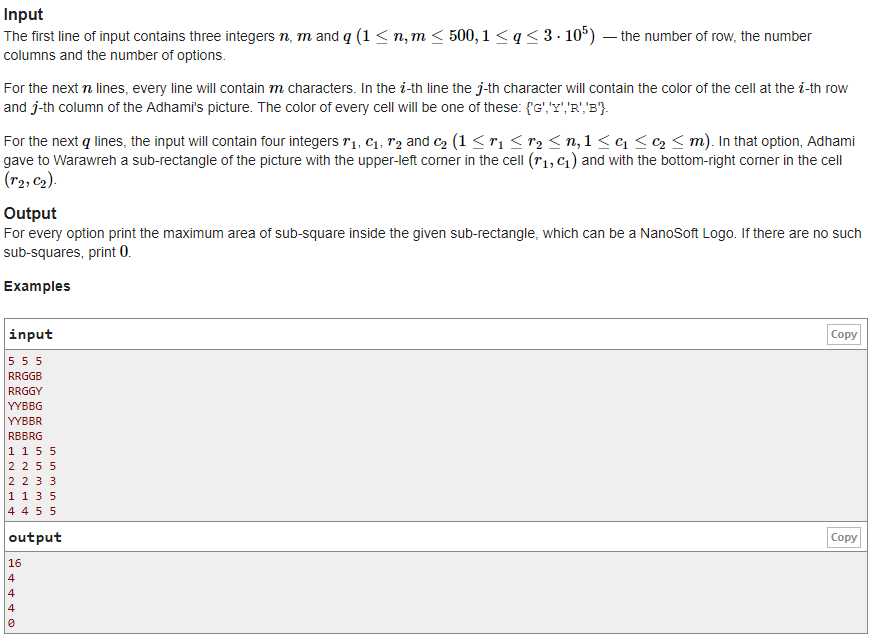
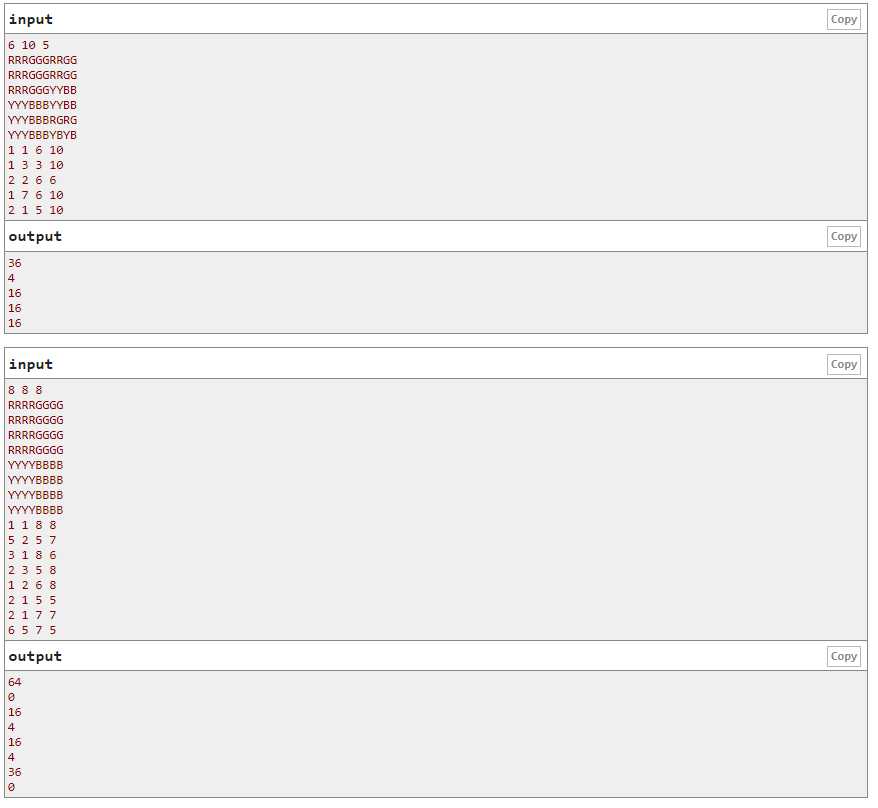
题意:求给定子矩阵中最大的合法颜色子矩阵,合法颜色子矩阵为大小(2*l)*(2*l)的矩阵,其中l为四种颜色矩阵的长度,详细合法颜色矩阵看题
题解:首先我们可以求出以每个点为中心时的最大合法颜色子矩阵是多少
然后用二维ST表存起来
每次询问时二分答案,根据答案可以推算出中心的的方位
注意到如果存在大小为l的合法颜色子矩阵,那么一定存在大小为l-1的合法颜色子矩阵
因此,直接查找区间里的值是否大于等于当前二分的值即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long #define red 1 #define green 2 #define yellow 3 #define blue 4 #define Max(a,b,c,d) max(a,max(b,max(c,d))) using namespace std; int n,m,q; char mp[501][501]; int cnt[501][501][5],f[501][501][10][10]; int getcnt(int r1,int c1,int r2,int c2,int k) { if(r1<1 || c1<1 || r2>n || c2>m || r1>r2 || c1>c2)return -1; return cnt[r2][c2][k]-cnt[r1-1][c2][k]-cnt[r2][c1-1][k]+cnt[r1-1][c1-1][k]; } bool check(int r,int c,int l) { int vr=getcnt(r-l+1,c-l+1,r,c,red),vg=getcnt(r-l+1,c+1,r,c+l,green); int vy=getcnt(r+1,c-l+1,r+l,c,yellow),vb=getcnt(r+1,c+1,r+l,c+l,blue); if(vr==l*l && vg==l*l && vy==l*l && vb==l*l)return 1; return 0; } int getf(int r,int c) { int tl=0,tr=min(n,m),mid; while(tl<tr) { mid=(tl+tr+1)>>1; if(check(r,c,mid))tl=mid; else tr=mid-1; } return tl; } int pw[11]; void rmq() { for(int jj=1;jj<10;jj++) for(int i=1;i<=n;i++) for(int j=1;j+pw[jj]-1<=m;j++) f[i][j][0][jj]=max(f[i][j][0][jj-1],f[i][j+pw[jj-1]][0][jj-1]); for(int ii=1;ii<10;ii++) for(int i=1;i+pw[ii]-1<=n;i++) for(int j=1;j<=m;j++) f[i][j][ii][0]=max(f[i][j][ii-1][0],f[i+pw[ii-1]][j][ii-1][0]); for(int ii=1;ii<10;ii++) for(int jj=1;jj<10;jj++) for(int i=1;i+pw[ii]-1<=n;i++) for(int j=1;j+pw[jj]-1<=m;j++) f[i][j][ii][jj]=Max(f[i][j][ii-1][jj-1],f[i+pw[ii-1]][j][ii-1][jj-1],f[i][j+pw[jj-1]][ii-1][jj-1],f[i+pw[ii-1]][j+pw[jj-1]][ii-1][jj-1]); } int ask(int r1,int c1,int r2,int c2) { if(r1<1 || c1<1 || r2>n || c2>m || r1>r2 || c1>c2)return -1; int p1=0,p2=0; while(r1+pw[p1]-1<=r2)p1++;p1--; while(c1+pw[p2]-1<=c2)p2++;p2--; return Max(f[r1][c1][p1][p2],f[r2-pw[p1]+1][c1][p1][p2],f[r1][c2-pw[p2]+1][p1][p2],f[r2-pw[p1]+1][c2-pw[p2]+1][p1][p2]); } bool check2(int r1,int c1,int r2,int c2,int l){return ask(r1,c1,r2,c2)>=l;} int getans(int r1,int c1,int r2,int c2) { int tl=0,tr=min(n,m),mid; while(tl<tr) { mid=(tl+tr+1)>>1; if(check2(r1+mid-1,c1+mid-1,r2-mid,c2-mid,mid))tl=mid; else tr=mid-1; } return tl*tl*4; } int main() { pw[0]=1;for(int i=1;i<=10;i++)pw[i]=pw[i-1]<<1; scanf("%d%d%d",&n,&m,&q); for(int i=0;i<n;i++)scanf("%s",mp[i]); for(int i=0;i<n;i++) for(int j=0;j<m;j++) { if(mp[i][j]==‘R‘)cnt[i+1][j+1][red]=1; if(mp[i][j]==‘G‘)cnt[i+1][j+1][green]=1; if(mp[i][j]==‘Y‘)cnt[i+1][j+1][yellow]=1; if(mp[i][j]==‘B‘)cnt[i+1][j+1][blue]=1; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) for(int k=1;k<=4;k++) cnt[i][j][k]+=cnt[i-1][j][k]+cnt[i][j-1][k]-cnt[i-1][j-1][k]; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) f[i][j][0][0]=getf(i,j); rmq(); int r1,r2,c1,c2; while(q--) { scanf("%d%d%d%d",&r1,&c1,&r2,&c2); printf("%d\n",getans(r1,c1,r2,c2)); } return 0; }
F. Super Jaber

待填坑
Codeforces Round #619 (Div. 2)/CF1301 【思维+贪心+模拟+构造+二维ST表】
标签:现在 turn 四种 void 均值 swa 子串 lld 图片
原文地址:https://www.cnblogs.com/worcher/p/12308153.html