模拟赛T2 仙人掌毒题

标签：tchar   模拟   fine   维护   oid   include   inf   long   print   

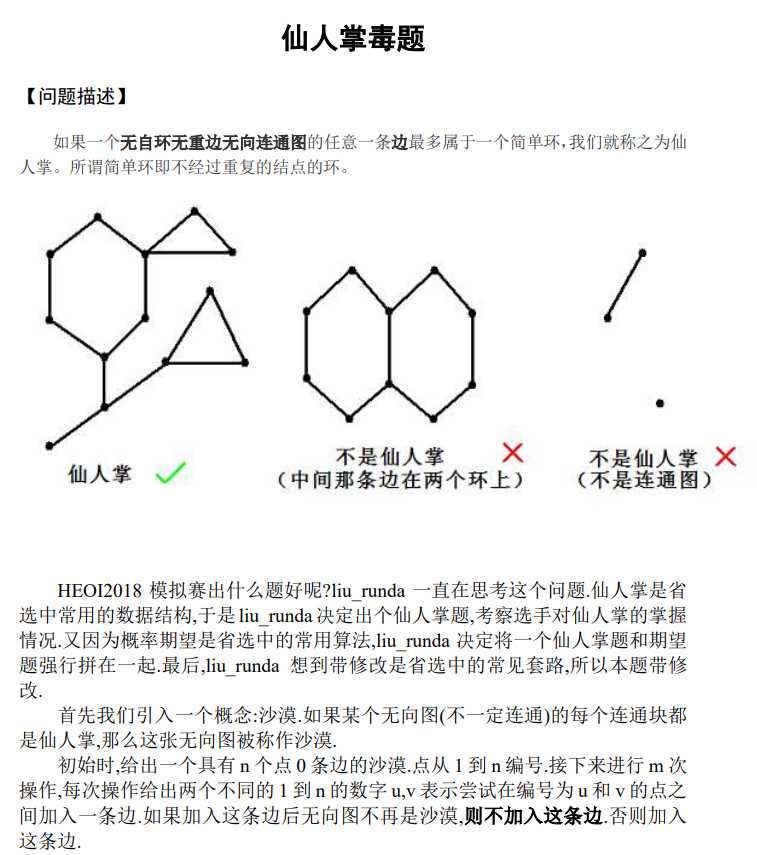
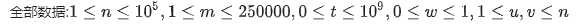
分析：
我们首先知道这样一个公式：
对于树：连通块=点-边
对于仙人掌：连通块=点-边+环
考虑期望的线性性：
连通块期望=点期望-边期望+环期望

对于点：
一个点T次标记后还为0的概率为\((\frac{n-1}{n})^T\)，为1就是\(1-(\frac{n-1}{n})^T\)
乘上系数n就是点期望

对于边：
一条边两边点都是0的概率为\((\frac{n-2}{n})^T\)
为1要容斥一下，概率为\(1-2(\frac{n-1}{n})^T+(\frac{n-2}{n})^T\)

然后就是重头戏
我们要维护仙人掌并讨论环：
一个大小为m的环中所有点为0的概率为\((\frac{n-m}{n})^T\)
为1的概率要进行容斥：
\(ans=\sum_{i=0}^{m}(-1)^iC_{m}^{i}(\frac{n-i}{n})^T\)
没必要什么花里胡哨NTT，暴力O(m)算平摊下来复杂度也只有O(n)，因为每条边只会存在于一个环中

然后就是维护仙人掌
喜 闻 乐 见的LCT维护圆方树
每次看链上的边是否已被一条额外边覆盖就好了

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<queue>

#define maxn 200005
#define INF 0x3f3f3f3f
#define MOD 998244353

using namespace std;

inline long long getint()
{
    long long num=0,flag=1;char c;
    while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
    while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
    return num*flag;
}

long long n,m,T,W,tot,invn;
long long fac[maxn],inv[maxn];
int sum[maxn],ch[maxn][2],fa[maxn],rev[maxn],stag[maxn],tag[maxn];
int stk[maxn],tp;
long long P,E,Cir;
int Q[maxn],sz;

inline long long C(long long p,long long q)
{return fac[p]*inv[q]%MOD*inv[p-q]%MOD;}

inline long long ksm(long long num,long long k)
{
    long long ret=1;
    for(;k;k>>=1,num=num*num%MOD)if(k&1)ret=ret*num%MOD;
    return ret;
}

inline bool isroot(int x)
{return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}

inline void pushup(int x)
{stag[x]=stag[ch[x][0]]|stag[ch[x][1]]|tag[x];}

inline void rv(int x)
{rev[x]^=1,swap(ch[x][0],ch[x][1]);}

inline void pushdown(int x)
{if(rev[x])rev[x]=0,rv(ch[x][0]),rv(ch[x][1]);}

inline void rotate(int x)
{
    int y=fa[x],z=(ch[fa[x]][1]==x);
    ch[y][z]=ch[x][z^1];
    if(ch[x][z^1])fa[ch[x][z^1]]=y;
    if(!isroot(y))ch[fa[y]][ch[fa[y]][1]==y]=x;
    fa[x]=fa[y];
    fa[y]=x;
    ch[x][z^1]=y;
    pushup(y);
}

inline void splay(int x)
{
    int tmp=x;
    while(!isroot(tmp))stk[++tp]=tmp,tmp=fa[tmp];
    stk[++tp]=tmp;
    while(tp)pushdown(stk[tp--]);
    while(!isroot(x))
    {
        if(!isroot(fa[x]))
        {
            if((ch[fa[x]][1]==x)==(ch[fa[fa[x]]][1]==fa[x]))rotate(fa[x]);
            else rotate(x);
        }
        rotate(x);
    }
}

inline void access(int x)
{for(int u=0;x;u=x,x=fa[x])splay(x),ch[x][1]=u,pushup(x);}

inline void makeroot(int x){access(x),splay(x),rv(x);}

inline void link(int x,int y)
{makeroot(x),access(x),splay(x),fa[x]=y;}

inline void cut(int x, int y)
{
    makeroot(x),access(y),splay(y);
    ch[y][0]=0,fa[x]=0,pushup(y);
}

inline bool check(int x,int y)
{
    makeroot(x),splay(x),access(y),splay(y);
    return !isroot(x);
}

inline void solve(int x)
{
    if(!x)return;
    pushdown(x);
    solve(ch[x][0]),Q[++sz]=x,solve(ch[x][1]);
}

inline long long calc(int sz)
{
    long long ret=0;
    for(int i=0;i<=sz;i++)
        (ret+=((i&1)?MOD-1:1)*C(sz,i)%MOD*ksm((n-i)*invn%MOD,T))%=MOD;
    return ret;
}

int main()
{
    n=getint(),m=getint(),T=getint(),W=getint();
    fac[0]=fac[1]=inv[0]=inv[1]=1;
    for(int i=2;i<maxn;i++)fac[i]=fac[i-1]*i%MOD;
    for(int i=2;i<maxn;i++)inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
    for(int i=2;i<maxn;i++)inv[i]=inv[i]*inv[i-1]%MOD;
    invn=ksm(n,MOD-2),tot=n;
    P=W?n:n*ksm((n-1)*invn%MOD,T)%MOD;
    while(m--)
    {
        int u=getint(),v=getint();
        int p=0;
        if(check(u,v))
        {
            makeroot(u),access(v),splay(v);
            if(!stag[v])
            {
                sz=0;solve(v);
                (Cir+=ksm((n-sz)*invn%MOD,T))%=MOD;
                if(W)(Cir+=calc(sz))%=MOD;
                tot++;
                tag[tot]=1;
                pushup(tot);
                for(int i=1;i<sz;i++)cut(Q[i],Q[i+1]),link(Q[i],tot);
                link(Q[sz],tot);
            }
            else p=1;
        }
        else link(u,v);
        if(!p)
        {
            (E+=ksm((n-2)*invn%MOD,T))%=MOD;
            if(W)(E+=1-2*ksm((n-1)*invn%MOD,T)%MOD+ksm((n-2)*invn%MOD,T)+MOD)%=MOD;
        }
        printf("%lld\n",(P-E+Cir+MOD)%MOD);
    }
}

模拟赛T2 仙人掌毒题

标签：tchar   模拟   fine   维护   oid   include   inf   long   print   

原文地址：https://www.cnblogs.com/Darknesses/p/12309598.html