标签:c代码 代码 出现 getchar inf 分代 getc orm ==
https://vjudge.net/problem/UVA-10572
给一个$n\times m$的棋盘,每个格子可以填成黑色或者白色,其中有些地方已经填了颜色,还有一些地方没有填颜色,要求
要把整个棋盘颜色填完,问有多少种填法
$2\leqslant n,m\leqslant 8$
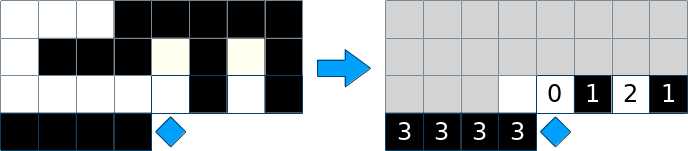
在轮廓线上记录这个格子属于的连通块编号和这个格子的颜色,为了保证不出现2,多记录一个左上角的颜色,那么就可以模拟2判断是否能转移,同时保证只会填和棋盘相同的颜色
保证所有相同颜色的格子连通可以分成两种情况
把新填的连通块记为9
如果新填的和相邻块颜色相同,就需要把所有的连通块编号进行替换
最后需要对连通块编号进行一次最小表示,可以减小许多状态。
书上的标程还有两个技巧,如果还剩两排就有连通块消失了,一定会出现$2\times2$的情况,就不继续转移了
如果左边和上面的颜色不同,对2的判断没有影响(对1的判断也同样没有影响),答案都是一样的,可以把状态合并,减少状态
由于状态表示很多,用了unordered_map进行记忆化
= =写了三天,最后还是照着训练指南的标程(https://github.com/klb3713/aoapc-book/blob/master/TrainingGuide/bookcodes/ch6/uva10572.cpp)写才过了……
然后又凭着记忆写了一遍,还是太菜了
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cctype>
#include<unordered_map>
#define REP(i,a,b) for(register int i=(a); i<(b); i++)
#define REPE(i,a,b) for(register int i=(a); i<=(b); i++)
#define PERE(i,a,b) for(register int i=(a); i>=(b); i--)
using namespace std;
typedef long long ll;
int nrow, ncol; //防止记忆混乱,m和n难以分清
char mp[8][8];
char tp[8][8], ap[8][8];
bool ok;
unordered_map<unsigned, int> dp[8][8][2];
char ch[]="o#";
struct node {
char colors[8];
char ltk[8];
char acolor;
char cnt[2];
void norm() {
int now=0;
int nltk[10];
memset(nltk,-1,sizeof(nltk));
memset(cnt,0,sizeof(cnt));
REP(i,0,ncol) {
if(nltk[ltk[i]]<0) {
nltk[ltk[i]]=now++;
cnt[colors[i]]++;
}
ltk[i]=nltk[ltk[i]];
}
}
unsigned encode() const {
unsigned ans=0;
REP(i,0,ncol) {
ans=(ans<<4) | (colors[i]<<3) | ltk[i];
}
return ans;
}
void replace(char f, char t) {
REP(i,0,ncol) if(ltk[i]==f) ltk[i]=t;
}
};
int calc(int r, int c, node &F, int f) {
//f表示剩下可以涂的颜色,如果是-1表示两种颜色都可以涂,可以复用一部分代码
//使用r和c而不是x和y的原因是防止记忆化的时候与初始化的顺序不同
if(c==ncol) {c=0, r++;}
if(r==nrow) {
if(F.cnt[0]>1 || F.cnt[1]>1) return 0;
if(!ok) {
ok=true;
memcpy(ap, tp, sizeof(tp));
}
return 1;
}
if(c && F.colors[c]!=F.colors[c-1]) {
F.acolor=0;
}
unsigned k;
if(f<0) {
k=F.encode();
if(dp[r][c][F.acolor].count(k)) return dp[r][c][F.acolor][k];
}
int ans=0;
REP(color,0,2) {
if(color == (f^1)) continue; //和可以涂的颜色不一样
if(color == (mp[r][c]^1)) continue; //和棋盘的颜色不一样
if(r && c && color == F.acolor && color == F.colors[c-1] && color == F.colors[c]) continue; //非第一排第一列出现了2x2
node T; memcpy(&T, &F, sizeof(node));
T.acolor = F.colors[c];
if(r==0 || color != F.colors[c]) T.ltk[c]=9;
T.colors[c] = color;
if(c && color==T.colors[c-1]) T.replace(T.ltk[c], T.ltk[c-1]);
tp[r][c]=ch[color];
if(r && color != F.colors[c] && find(T.ltk, T.ltk+ncol, F.ltk[c])==T.ltk+ncol) { //非第一排,消失了连通块
if(F.cnt[color^1]>1 || nrow-r>2) { //except this+剪枝
continue;
}
T.norm();
ans += calc(r, c+1, T, color);
continue;
}
T.norm();
ans += calc(r, c+1, T, f);
}
if(f<0) dp[r][c][F.acolor][k]=ans;
return ans;
}
int main() {
int T; scanf("%d", &T);
while(0<T--) {
scanf("%d%d", &nrow, &ncol);
REP(i,0,nrow) REP(j,0,ncol) do mp[i][j]=getchar(); while(mp[i][j]<=‘ ‘);
REP(i,0,nrow) REP(j,0,ncol) switch(mp[i][j]) {
case ‘o‘: mp[i][j]=0; break;
case ‘#‘: mp[i][j]=1; break;
default: mp[i][j]=2; break;
}
REP(i,0,nrow) REP(j,0,ncol) REP(k,0,2) dp[i][j][k].clear();
ok=false;
node F; memset(&F,0,sizeof(F)); //假设第-1排全部涂成白色,不管怎么样,对1和2的判断没有影响
int ans = calc(0,0,F,-1);
printf("%d\n", ans);
if(ok) REP(i,0,nrow) {
REP(j,0,ncol) putchar(ap[i][j]);
putchar(‘\n‘);
}
putchar(‘\n‘);
}
}
暂坑= =
标签:c代码 代码 出现 getchar inf 分代 getc orm ==
原文地址:https://www.cnblogs.com/sahdsg/p/12309773.html