标签:code ons png MLOG puts one 完美 second http
考试时有个费用流的思路,但是爆0了,考后看到有人拿这个得了60分,应该是自己打错了,但看不出来.
题意:n堆石子,每堆石子有ai个,m次指令,每次指令要求把li,ri内的石子拿ki个,如果不够可以全拿,求拿的石子的最大字典序。保证区间互不包含。n=3e5 m=3e5 ai=500 ki=10000
题解:好神的霍尔定理用法啊,没想到它还能这样用...
把指令按照li排序,把每个指令拆成ki个,把每堆石头拆成ai个。设每个指令的答案为B[i],那么用霍尔定理检验的话就是检验是由有完美匹配。
由于题目保证互不包含,因此如果使用霍尔定理的话,原定理:“如果X存在完美匹配,那么对于任意子集|S|和对应的连边集合|T|都有|S|<=|T|。“
就可以将任意子集转化成连续的几个指令,原因:考虑不连续的若干个指令,这里只考虑两个的情况,大于两个的情况可以连续的指令两两间考虑来达到目的。
如果说这两个指令的区间相离,只需要检验分别这两个指令是否合法;
如果两个指令相交,那么由于互不包含的特殊性质,把这两个指令中间的指令加入|S|,|T|不变,这时的条件比原条件更为苛刻。
对于每次指令,是要求所有包含这个指令的区间都符合条件,即
$$\sum\limits_{l=1}^{p[i]}\sum\limits_{r=p[i]}^m sumB[r]-sumB[l-1]<=sumA[R[r]]-sumA[L[l]-1]$$
$$sumB[r]-sumA[R[r]]<=sumB[l-1]-sumA[L[l]-1]$$
线段树上维护每个点最大的sumB[i]-sumA[R[i]]与最小的sumB[i-1]-sumA[L[i]-1],查询时查询max p[i]~m sumB[i]-sumA[R[i]],min 1~p[i] sumB[i-1]-sumA[L[i]-1],再用min-max就是答案。
要和ki取min。
复杂度O(mlog)。

#include<bits/stdc++.h> #define ll long long using namespace std; const int N=3e5+50; inline int rd(register int x=0,register char ch=getchar(),register int f=0){ while(!isdigit(ch)) f=ch==‘-‘,ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar(); return f?-x:x; } int n,m; int a[N],cf[N],ans[N],I[N]; ll sum[N],C[N<<2],D[N<<2],tagC[N<<2],tagD[N<<2],sc[N],sd[N]; struct O{int l,r,id;}dat[N]; bool cmp(O a,O b){return a.l<b.l;} #define lch k<<1 #define rch k<<1|1 //C维护最小值,D维护最大值 void down(int k){ if(tagC[k]) C[lch]+=tagC[k],C[rch]+=tagC[k],tagC[lch]+=tagC[k],tagC[rch]+=tagC[k],tagC[k]=0; if(tagD[k]) D[lch]+=tagD[k],D[rch]+=tagD[k],tagD[lch]+=tagD[k],tagD[rch]+=tagD[k],tagD[k]=0; } void add(int k,int l,int r,int L,int R,int opt,int e){//0是C,1是D if(L>R) return; if(L<=l&&r<=R) return opt?(D[k]+=e,tagD[k]+=e):(C[k]+=e,tagC[k]+=e)/*,printf("!%d %d %d %d %d %d %lld %lld\n",l,r,L,R,opt,e,C[k],D[k])*/,void(); int mid=(l+r)>>1;down(k); if(L<=mid) add(lch,l,mid,L,R,opt,e); if(R>mid) add(rch,mid+1,r,L,R,opt,e); C[k]=min(C[lch],C[rch]),D[k]=max(D[lch],D[rch]); } ll g(int opt,ll res,ll querY){return opt?max(res,querY):min(res,querY);} ll query(int k,int l,int r,int L,int R,int opt){ if(L<=l&&r<=R) return opt?D[k]:C[k]; int mid=(l+r)>>1;down(k); ll res=opt?-0x3f3f3f3f3f3f3f3f:0x3f3f3f3f3f3f3f3f; if(L<=mid) res=g(opt,res,query(lch,l,mid,L,R,opt)); if(R>mid) res=g(opt,res,query(rch,mid+1,r,L,R,opt)); return res; } void build(int k,int l,int r){ if(l==r) return C[k]=sc[dat[l].id],D[k]=sd[dat[l].id],void(); int mid=(l+r)>>1;build(lch,l,mid),build(rch,mid+1,r); C[k]=min(C[lch],C[rch]),D[k]=max(D[lch],D[rch]); } #undef lch #undef rch int main(){ n=rd();for(int i=1;i<=n;++i) a[i]=rd();m=rd();for(int i=1;i<=m;++i) dat[i].l=rd(),dat[i].r=rd(),ans[i]=rd(),dat[i].id=i,cf[dat[i].l]++,cf[dat[i].r+1]--; sort(dat+1,dat+m+1,cmp);for(int i=1;i<=m;++i) I[dat[i].id]=i; for(int i=1;i<=n;++i) cf[i]+=cf[i-1],sum[i]=sum[i-1]+(cf[i]>0?a[i]:0); for(int i=1;i<=m;++i) sd[i]=-sum[dat[I[i]].r],sc[i]=-sum[dat[I[i]].l-1]; build(1,1,m); for(int i=1;i<=m;++i){ ll rx=query(1,1,m,I[i],m,1),ln=query(1,1,m,1,I[i],0); printf("%d\n",ans[i]=min(0ll+ans[i],ln-rx)); add(1,1,m,I[i],m,1,ans[i]);add(1,1,m,I[i]+1,m,0,ans[i]); //for(int j=1;j<=m;++j) printf("C[%d]=%lld D[%d]=%lld\n",j,query(1,1,m,j,j,0),j,query(1,1,m,j,j,1));puts(""); } return 0; }
不会枯了
题意:同圈地游戏。
题解:可以发现(?)最终路线一定不会穿过从起点到每个特殊点的左上端点的最短路,如果穿过就完全可以顺着最短路走。
所以需要找到一条包裹所有最短路的环,使得环长最小。
那么对每个点建出四个点
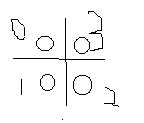
然后对应的向四周连边
假如说有某条边不能经过,那么它上下(左右)的两个点就不能连边(如上边的边lim=1,则0 3不能连边,表示不能这样走)
注意,特殊点由于不能经过,因此特殊点内部的四个点不能连边。
注意,(1,1)的(0,1),(0,3)不能连边,答案就是s=(1,1,3)t=(1,1,1)的最短路。

#include<bits/stdc++.h> #define ll long long using namespace std; const int N=405; inline int rd(register int x=0,register char ch=getchar(),register int f=0){ while(!isdigit(ch)) f=ch==‘-‘,ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar(); return f?-x:x; } const int sx[4]={0,0,1,-1},sy[4]={1,-1,0,0}; int n,m,B,head[N*N*4],to[N*N*16],nxt[N*N*16],vis[N*N*4],nw[N*N][4],al[N*N][4]; ll s[N][N],dis[N*N],pre[N*N],w[N*N*16]; map<int,int>lim[N*N],a[N*N]; pair<int,int> rem(int x){return make_pair((x-1)/m+1,(x-1)%m+1);} bool check(int x,int y){return (x<=0||x>n||y<=0||y>m)?0:1;} int id(int x,int y){return check(x,y)?(x-1)*m+y:0;} void lnk(int x,int y,int value){if(!x||!y) return ; to[++B]=y,nxt[B]=head[x],head[x]=B,w[B]=value; } int main(){ n=rd();m=rd();n++;m++;//点的数量是块的数量+1 for(int i=1;i<=n-1;++i) for(int j=1;j<=m-1;++j) s[i][j]=rd(); for(int i=1;i<=n-1;++i) for(int j=1;j<=m;++j) a[id(i,j)][id(i+1,j)]=a[id(i+1,j)][id(i,j)]=rd(); for(int i=1;i<=n;++i) for(int j=1;j<=m-1;++j) a[id(i,j)][id(i,j+1)]=a[id(i,j+1)][id(i,j)]=rd(); for(int i=1;i<=n*m;++i) dis[i]=0x3f3f3f3f3f3f3f3f,vis[i]=0; priority_queue<pair<ll,int> >q;q.push(make_pair(dis[1]=0,1)); while(!q.empty()){ int u=q.top().second;q.pop(); if(vis[u]) continue;vis[u]=1; pair<int,int>A=rem(u); for(int i=0,I;i<4;++i) if(check(A.first+sx[i],A.second+sy[i])&&dis[I=id(A.first+sx[i],A.second+sy[i])]>dis[u]+a[u][I]) pre[I]=u,q.push(make_pair(-(dis[I]=dis[u]+a[u][I]),I)); } for(int i=1;i<=n-1;++i) for(int j=1;j<=m-1;++j) if(s[i][j]){ int I=id(i,j),J; while(I!=1) J=pre[I],lim[I][J]=lim[J][I]=1,I=J; } int tot=0;for(int i=1;i<=n*m;++i) for(int j=0;j<4;++j) nw[i][j]=++tot; al[id(1,1)][0]=1; for(int i=1;i<=n-1;++i) for(int j=1;j<=m-1;++j) if(s[i][j]) al[id(i,j)][2]=al[id(i+1,j)][3]=al[id(i,j+1)][1]=al[id(i+1,j+1)][0]=1; for(int i=1;i<=n;++i) for(int j=1;j<=m;++j){ int I=id(i,j),J; if(!al[I][0]&&!al[I][3]&&!lim[I][id(i-1,j)]) lnk(nw[I][0],nw[I][3],0),lnk(nw[I][3],nw[I][0],0); if(!al[I][0]&&!al[I][1]&&!lim[I][id(i,j-1)]) lnk(nw[I][0],nw[I][1],0),lnk(nw[I][1],nw[I][0],0); if(!al[I][1]&&!al[I][2]&&!lim[I][id(i+1,j)]) lnk(nw[I][1],nw[I][2],0),lnk(nw[I][2],nw[I][1],0); if(!al[I][2]&&!al[I][3]&&!lim[I][id(i,j+1)]) lnk(nw[I][2],nw[I][3],0),lnk(nw[I][3],nw[I][2],0); if(j-1>=1){J=id(i,j-1); if(!al[I][0]&&!al[J][3]) lnk(nw[I][0],nw[J][3],a[J][I]); if(!al[I][1]&&!al[J][2]) lnk(nw[I][1],nw[J][2],a[J][I]); } if(j+1<=m){J=id(i,j+1); if(!al[I][3]&&!al[J][0]) lnk(nw[I][3],nw[J][0],a[J][I]); if(!al[I][2]&&!al[J][1]) lnk(nw[I][2],nw[J][1],a[J][I]); } if(i-1>=1){J=id(i-1,j); if(!al[I][0]&&!al[J][1]) lnk(nw[I][0],nw[J][1],a[J][I]); if(!al[I][3]&&!al[J][2]) lnk(nw[I][3],nw[J][2],a[J][I]); } if(i+1<=n){J=id(i+1,j); if(!al[I][1]&&!al[J][0]) lnk(nw[I][1],nw[J][0],a[J][I]); if(!al[I][2]&&!al[J][3]) lnk(nw[I][2],nw[J][3],a[J][I]); } } for(int i=1;i<=tot;++i) dis[i]=0x3f3f3f3f3f3f3f3f,vis[i]=0; q.push(make_pair(dis[nw[1][3]]=0,nw[1][3])); while(!q.empty()){ int u=q.top().second;q.pop(); if(vis[u]) continue;vis[u]=1; for(int i=head[u];i;i=nxt[i]) if(dis[to[i]]>dis[u]+w[i]) q.push(make_pair(-(dis[to[i]]=dis[u]+w[i]),to[i])); } printf("%lld\n",dis[nw[1][1]]); return 0; }
细节还行,打完后一遍过的。
标签:code ons png MLOG puts one 完美 second http
原文地址:https://www.cnblogs.com/hzoi2018-xuefeng/p/12310577.html