标签:date 规则 精度 根据 正数 down 运算 code symbol
今天,发生一件非常有趣的事情。
公司同事问了我一个问题:为什么 2.0 - 1.1 = 0.89999999 呢?不应该是 0.9吗?
原来是,他问了周围一圈的同事,都给他的是同一个回答,说这是精度问题。他百思不得其解,怎么就会产生精度问题呢。再问,就没人知道原因了。
然后,我就看到了他抱着一本厚厚的书在看。拿过来一看,是一本Java书,厚厚的六百多页,这还仅是第一卷。哟呵,这是准备大干一场啊。
看在他这么努力学习的份上,还有他那对知识极度渴望的眼神。我决定,把我毕生所学传授与他。
于是,就给他详细讲解了,计算机中是怎么存储一个数的,十进制是怎么在转二进制的过程中丢失精度的,以及浮点数是怎么遵循IEEE 754 规范的,在浮点数进行加减运算的过程中会经历对阶、移位运算等过程,以及在此过程中是怎么丢失精度的。(这些问题在之前的文章中都有解答,参看“为什么0.1+0.2=0.30000000000000004”)
然后,成功的把他彻底搞懵逼了。怎么这么难啊。
原来,他的计算机基础比我还匮乏,不知道什么是位运算,不知道什么是原码、反码和补码。
本着我的热心肠,我就给他普及了一下这些知识 ---- 负数的补码形式和位移运算。
我们知道,一个数分为有符号和无符号。对于,有符号的数来说,最高位代表符号位,即最高位1代表负数,0代表正数。
在计算机中,存储一个数的时候,都是以补码的形式存储的。而正数和负数的补码表示方式是不一样的。正数的补码就等于它的原码,而负数的补码是原码除符号位以外都取反,然后 + 1 得来的。以一个int类型为例(4个字节即32位)
14的原码为:
0000 0000 0000 0000 0000 0000 0000 1110它的反码、补码和原码都是一样的。
-14的原码为:
//最高位1为符号位,代表此数为负数
1000 0000 0000 0000 0000 0000 0000 1110反码为原码除了符号位以外的其他位都取反(即0变为1,1变为0),
1111 1111 1111 1111 1111 1111 1111 0001补码为反码 + 1 ,注意二进制中是满二进一。
1111 1111 1111 1111 1111 1111 1111 0010位的左移,右移运算就是分别向左和向右移动N位。移位的规则是:
因左移就在右边低位补0就可以了,比较简单,我就以负数的右移来举例,是怎么计算无符号右移和带符号右移的。还是以 -14 为例。
// -14的补码
1111 1111 1111 1111 1111 1111 1111 0010
// 带符号右移用 >> 表示,即右移一位 -14>>1,高位补符号位1,低位舍去
1111 1111 1111 1111 1111 1111 1111 1001
// 无符号右移用 >>> 表示,即右移一位 -14>>>1,最高位补0
0111 1111 1111 1111 1111 1111 1111 1001我们可以通过程序来验证一下 -14>>1和 -14>>>1的结果是否正确。
1. -14>>1 = -7
//我们算出来 -14>>1的补码为:
1111 1111 1111 1111 1111 1111 1111 1001
//那它具体代表的数值是多少呢?
//首先,补码 -1 得到反码
1111 1111 1111 1111 1111 1111 1111 1000
//然后,反码取反得到原码,最高位符号位不变
1000 0000 0000 0000 0000 0000 0000 0111这结果不就是 -7 吗,然后通过程序计算一下结果:
public class TestMove {
public static void main(String[] args) {
System.out.println( -14>>1);
}
}结果同样也是-7 。说明了我们位移操作没问题。
2. -14>>>1=2147483641
我们通过一段程序去验证:
package com.test.binary;
?
/**
* @Author zwb
* @DATE 2019/12/3 15:49
*/
public class TestBinary {
public static void main(String[] args) {
//我们自己计算出来的 -14>>>1 结果
String bin = "01111111111111111111111111111001";
double res = binToDec(bin);
System.out.println(res);
//通过计算机计算的结果
System.out.println(-14>>>1);
}
?
//二进制转为十进制
public static double binToDec(String bin){
int index = bin.indexOf(".");
int len = bin.length();
double res = 0;
//index为-1说明没有小数
if(index == -1){
for(int i = 0; i< len; i++){
res += Math.pow(2,i) * Integer.parseInt(String.valueOf(bin.charAt(len-1-i)));
}
}else{
//整数部分
int partA = 0;
for(int i = 0; i< index; i++){
partA += Math.pow(2,i) * Integer.parseInt(String.valueOf(bin.charAt(index-1-i)));
}
//小数部分
double partB = 0;
for(int j = index + 1; j < len; j++){
partB += Math.pow(2,index - j) * Integer.parseInt(String.valueOf(bin.charAt(j)));
}
res = partA + partB;
}
return res;
}
}运行之后的结果,可以在控制台打印看到: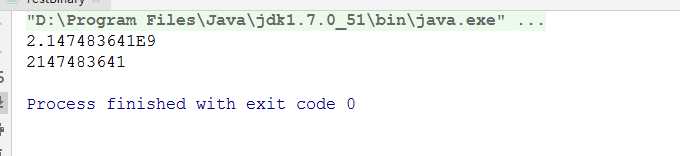
上边第一个是我们自己通过推算它的补码,然后通过二进制转十进制的一个算法算出来的最终结果,第二个就是直接通过位运算算出来的结果。可以看到结果是一模一样的。
至此,是不是对原码,反码,补码以及位运算左移右移,有了比较清晰的认识了呢?
今天,我们深入探讨一下,为什么计算机中要用补码来表示负数?
首先,我们应该清楚,原码是方便给人看的。看到一个数的原码,我们就能根据符号位和后边的二进制位,计算出这个数的实际值。为了简单起见,我以一个字节8位来举例,如
// 1 的原码 ,最高位0代表正数
0000 0001
// -1 的原码, 最高位1代表负数
1000 0001可以看到,1和 -1 的原码只有符号位不同。然后,思考一个问题,1 - 1 = ?
是的,我们可以直接通过减法去计算,得出1-1=0 。但是,做减法运算时,可能会遇到不够减而需要借位的情况,这显然是比较麻烦的。我们换一种思路。 1-1 在数学中等同于 1+(-1)。这样,把减法转换为加法就简单的多了,只需要考虑进位就可以了。(其实,计算机中只有加法器,没有减法器,因此减法是通过加法器来计算的。)
于是,我们看下,把1和-1的原码相加等于多少(需要让符号位也参与运算)
0000 0001
+ 1000 0001
1000 0010结果是 -2 ,这显然不符合我们的预期。
为了解决原码减法的问题,于是,出现了反码。使用反码,再来计算一下。
// 1的反码,同原码
0000 0001
// -1的反码,符号位不变,其他取反
1111 1110相加之后,得 1111 1111 ,这是反码,转为原码为 1000 0000 ,即为 -0 。
但是,这又有问题了,在数学中0就是0,怎么到这还有 -0,+0之分。按照原码的概念来算,+0的原码为0000 0000 , -0 的原码为 1000 0000 。问题就出在这了,如果遇到0的计算,是应该用 +0 还是用 -0 计算呢,这就会产生分歧。于是,补码出现了,解决了0的符号问题 。
// 1的补码,同原码
0000 0001
// -1的补码,反码 +1
1111 1111相加得 1 0000 0000 ,最高位进位之后,超过了8位,于是舍去,即为0000 0000。此为补码,转为原码也是0000 0000 ,这不就是0 吗。
这样一来,用补码0000 0000来表示0,就解决了+0和-0在原码上的分歧,统一了0的二进制表示方法。
那,又有疑问了,-0跑哪去了呢? 其实,-0即1000 0000在这用来表示 -128。但是,注意表示的是 -128的补码,因此 -128没有原码和反码。
那为什么用 1000 0000表示 -128呢 ?
先看下 -127 的原码、反码和补码:
原码: 1111 1111
反码: 1000 0000
补码: 1000 0001
我们知道数学中 -127 -1 = -128 ,所以 -127的补码 -1 也应该等于 -128的补码,即
1000 0001 -1 = 1000 0000。因此1000 0000就是 -128的补码。
在一个字节8位中,如果用原码来表示值的大小范围,只能是 1111 1111 ~ 0111 1111,即-127~127 。但是,如果用补码就可以表示 -128~127,正好是2^8,256个数。
因此,-0可以表示一个最低数。在8位二进制中它是1000 0000 ,在32位中,它就是 1000 0000 0000 0000 0000 0000 0000 0000 ,int的最小值。(32位数值大小范围为 -2^31 ~ 2^31 -1)
总结:补码的存在解决了0的符号问题,同时统一了计算机的加减法运算。
标签:date 规则 精度 根据 正数 down 运算 code symbol
原文地址:https://www.cnblogs.com/Leo_wl/p/12315402.html