罗德里格斯旋转公式（Rodrigues' rotation formula）推导

标签：空间   视觉   定义   法则   结合   mic   oss   lin   坐标轴   

　　本文综合了几个相关的维基百科，加了点自己的理解，从比较基础的向量投影和叉积讲起，推导出罗德里格斯旋转公式。公式比较繁杂，如有错误，欢迎评论区指出。

　　对于向量的三维旋转问题，给定旋转轴和旋转角度，用罗德里格斯（Rodrigues）旋转公式可以得出旋转后的向量。另外，罗德里格斯旋转公式可以用旋转矩阵表示，即将三维旋转的轴-角（axis-angle）表示转变为旋转矩阵表示。

向量投影（Vector projection）

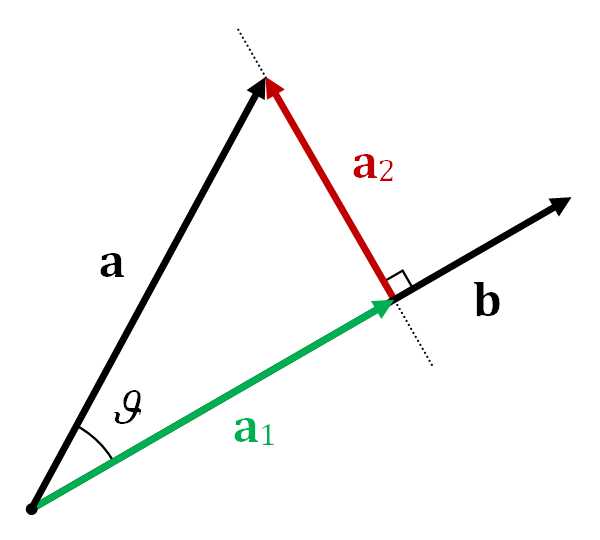
　　向量a在非零向量b上的向量投影指的是a在平行于向量b的直线上的正交投影。结果是一个平行于b的向量，定义为\(\mathbf{a}_1=a_1\hat{\mathbf{b}}\)，其中，\(a_1\)是一个标量，称为a在b上的标量投影，\(\hat{\mathbf{b}}\)是与b同向的单位向量。\(a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\mathbf{a}\cdot \hat{\mathbf{b}}=\mathbf{a}\cdot\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}\)，其中\(\cdot\)表示点积，\(\left\Vert\mathbf{a}\right\Vert\)表示a的长度，\(\theta\)表示a和b的夹角。标量投影有正负，正负号与夹角\(\theta\)有关。

　　有了向量投影\(\textbf{a}_1\)，向量a可以表示为\(\mathbf{a}=\mathbf{a}_1+\mathbf{a}_2\)，其中\(\mathbf{a}_2\)称为a from b的vector rejection（没找到比较官方的翻译），也即a向正交于b的超平面的正交投影，\(\mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-(\left\Vert\mathbf{a}\right\Vert\cos\theta)\hat{\mathbf{b}}\)。下图比较清晰地表示出\(\mathbf{a}\)、\(\mathbf{a}_1\)、\(\mathbf{a}_2\)的关系。

　　当\(90^{\circ}<\theta\le180^{\circ}\)时，向量投影示意图如图2所示：

记号

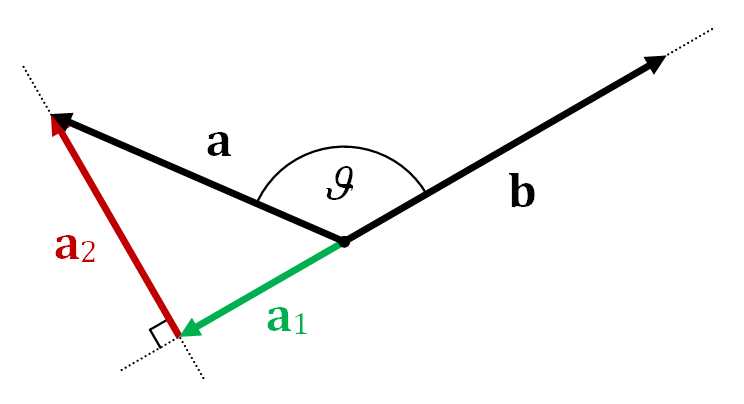
　　向量a在b上的向量投影用加粗的\(\mathbf{a}_1\)表示，标量投影用不加粗的\(a_1\)。有时向量投影和vector rejection分别用\(\mathbf{a}_{\parallel\mathbf{b}}\)和\(\mathbf{a}_{\perp\mathbf{b}}\)表示。

用a和b表示

　　当\(\theta\)未知时，可通过a和b计算得出，\(\cos\theta = \frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}\)，从而标量投影、向量投影和vector rejection可以分别表示如下：

• 标量投影：
  

  
  \begin{equation}
  a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\left\Vert\mathbf{a}\right\Vert\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}
  \end{equation}
  

• 向量投影：
  

  
  \begin{equation}
  \mathbf{a}_1=a_1\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}=\left(\mathbf{a}\cdot\hat{\mathbf{b}}\right)\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
  \end{equation}
  

• vector rejection：
  

  
  \begin{equation}
  \mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
  \end{equation}
  

叉积

定义

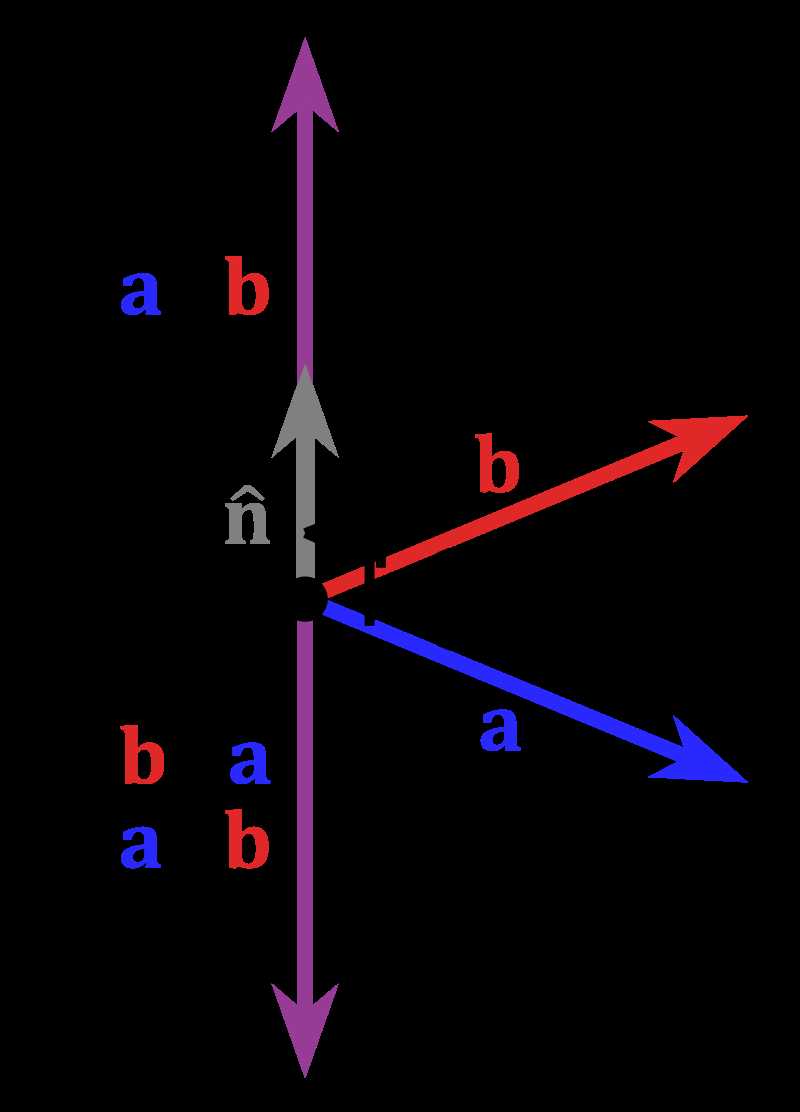
　　叉积（又称向量积）是三维空间（\(\mathbb{R}^3\)）向量的二元操作，用符号\(\times\)表示，给定两个线性独立的向量a和b，叉积\(\mathbf{a}\times\mathbf{b}\)的结果是一个向量，这个向量与a、b都正交，也就是正交于a、b所在的平面。为什么要强调线性独立呢，因为非线性独立的两个向量（同向或反向）的叉积为\(\mathbf{0}\)。

　　叉积定义为：

\begin{equation}
\mathbf{a}\times\mathbf{b}=\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert\sin(\theta)\mathbf{n}
\end{equation}

性质

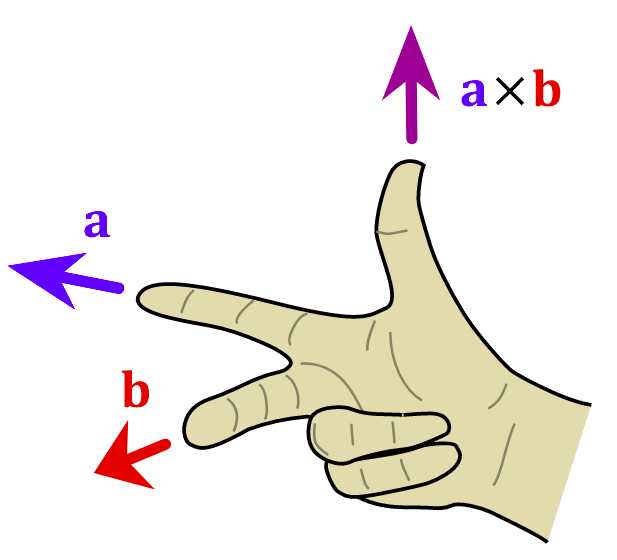
　　右手法则决定了叉积不符合交换律，而符合反交换律，即\(\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}\)，如图4所示：

　　由公式也可以看出当a、b的不线性独立时，即夹角为\(0^\circ\)或\(180^\circ\)时，叉积为零向量\(\mathbf{0}\)。叉积随夹角\(\theta\)的变化如图5所示。

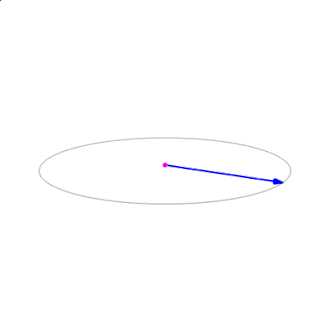
　　另外，叉积符合分配律，即\(\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}\)。如图6所示，左图向量b和c都被分解为vector projection和vector rejection两部分，右图则解释了分配律成立的原因，看图时要注意图中的平行四边形和正方形都表示了相等的关系。

坐标表示

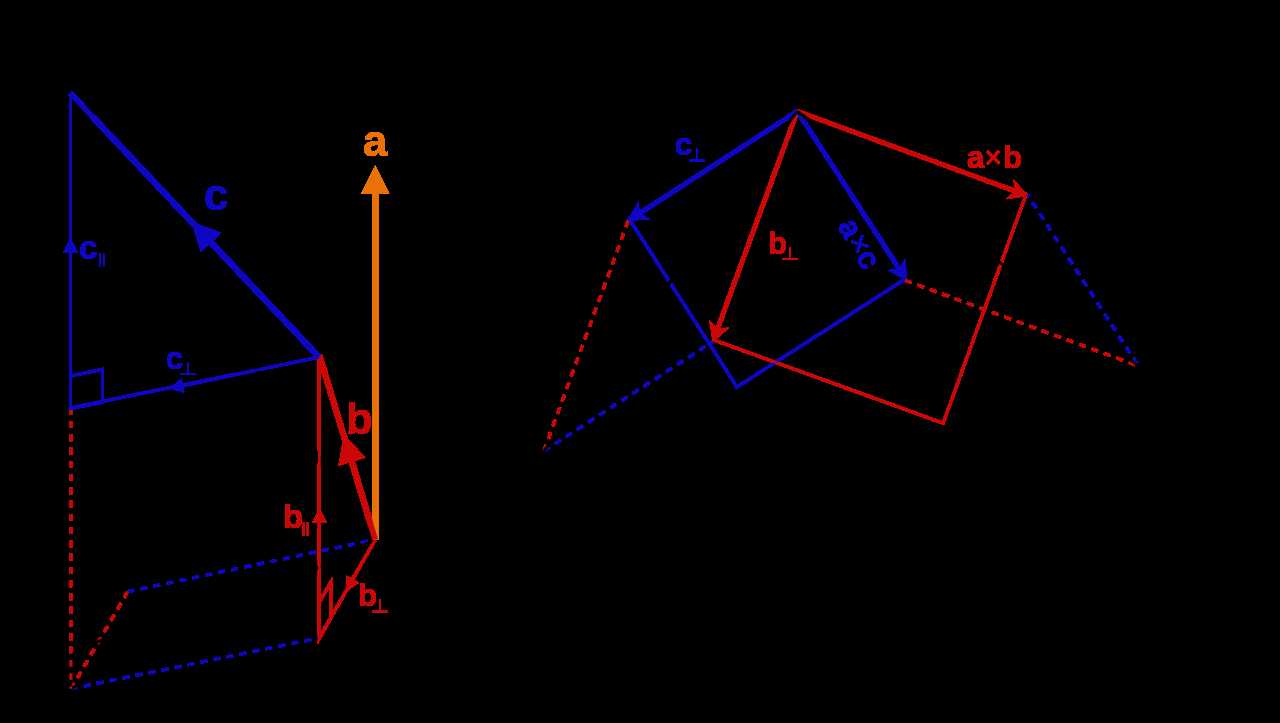
　　考虑右手法则定义的标准三维坐标系，三个坐标轴\(\mathbf{i}\)、\(\mathbf{j}\)、\(\mathbf{{k}}\)如图7所示，并满足以下等式关系：
\[ \mathbf{i}\times\mathbf{j}=\mathbf{k}\\mathbf{j}\times\mathbf{k}=\mathbf{i}\\mathbf{k}\times\mathbf{i}=\mathbf{j} \]
同样，由叉积的反交换律可得下面三个等式关系：
\[ \mathbf{j}\times\mathbf{i}=-\mathbf{k}\\mathbf{k}\times\mathbf{j}=-\mathbf{i}\\mathbf{i}\times\mathbf{k}=-\mathbf{j} \]
由平行向量的叉积为零向量可得：\(\mathbf{i}\times\mathbf{i}=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k}=\mathbf{0}\)。
　　由图7也可得，任意一个三维向量都可以表示为三个基向量的线性组合，例如：
\[ \mathbf{a}=a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k}\\mathbf{b}=b_1\mathbf{i}+b_2\mathbf{j}+b_2\mathbf{k} \]

　　进而，可以用坐标表示叉积运算如下：

\begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}&=(a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k})\times(b_1\mathbf{i}+b_2\mathbf{j}+b_2\mathbf{k})\&=(a_2b_3-a_3b_2)\mathbf{i}+(a_3b_1-a_1b_3)\mathbf{j}+(a_1b_2-a_2b_1)\mathbf{k}\&=\left|\begin{array}{cccc} i & j & k \\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array}\right| \end{split} \end{equation}

上式中，将括号展开分别进行叉积推导出第二个等号，而第三个等号则可通过行列式计算得出。
　　进一步，可将叉积表示为矩阵与向量相乘的形式，由于\(\mathbf{a}\times\mathbf{b}=(a_2b_3-a_3b_2, a_3b_1-a_1b_3,a_1b_2-a_2b_1)\)，则叉积可表示为：

\begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}=\left[\mathbf{a}\right]_\times\mathbf{b}=\left[\begin{array}{cccc} 0 & -a_3 & a_2\a_3 & 0 & -a_1\-a_2 & a_1 & 0 \end{array} \right]\left[ \begin{array}{cc} b_1\\b_2\\b_3 \end{array}\right]=\left[\mathbf{b}\right]^T_\times\mathbf{a}=\left[\begin{array}{cccc} 0 & b_3 & -b_2\-b_3 & 0 & b_1\b_2 & -b_1 & 0 \end{array} \right]\left[ \begin{array}{cc} a_1\\a_2\\a_3 \end{array}\right] \end{split} \end{equation}

其中，\(\left[\mathbf{a}\right]_\times\)（slam14讲书上记为\(\mathbf{a}^\wedge\)）表示由向量\(\mathbf{a}\)得到的反对称矩阵，定义为：

\begin{equation} \begin{split} \left[\mathbf{a}\right]_\times=\left[\begin{array}{cccc} 0 & -a_3 & a_2\a_3 & 0 & -a_1\-a_2 & a_1 & 0 \end{array} \right] \end{split} \end{equation}

通过该反对称矩阵的定义可以将叉积表示为矩阵与向量的乘法。

罗德里格斯旋转公式

　　考虑\(\mathbf{v}\in\mathbb{R}^3\)的三维旋转问题，旋转轴\(\mathbf{k}\)是单位向量，旋转角为\(\theta\)，按照右手法则（即逆时针）旋转。则可通过罗德里格斯旋转公式得出旋转后的向量\(\mathbf{v}_{rot}\)为：

\begin{equation} \mathbf{v}_{rot}=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{equation}

推导过程

　　由上文中向量投影部分的知识我们知道，一个向量\(\mathbf{v}\)可以分解为平行于\(\mathbf{k}\)的分量\(\mathbf{v}_\parallel\)和正交于\(\mathbf{k}\)的分量\(\mathbf{v}_{\perp}\)：

\begin{equation} \mathbf{v}=\mathbf{v}_{\parallel}+\mathbf{v}_\perp \end{equation}

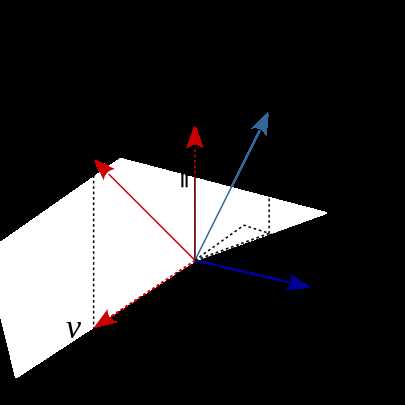
如图8所示，因为\(\mathbf{k}\)为单位向量，由向量投影部分知识可得

\begin{equation} \mathbf{v}_\parallel=(\mathbf{v}\cdot\mathbf{k})\mathbf{k} \end{equation}

\begin{equation} \mathbf{v}_\perp=\mathbf{v}-\mathbf{v}_\parallel=\mathbf{v}-(\mathbf{k}\cdot\mathbf{v})\mathbf{k}=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v}) \end{equation}

关于上式最后一个等号的推导如下：

　　回顾叉积的知识，\(\mathbf{k}\times\mathbf{v}=\mathbf{k}\times(\mathbf{v}_{\parallel}+\mathbf{v}_\perp)=\mathbf{0}+\mathbf{k}\times\mathbf{v}_\perp=\mathbf{k}\times\mathbf{v}_\perp\)，\(\mathbf{k}\times\mathbf{v}\)可以看做将\(\mathbf{v}_\perp\)以\(\mathbf{k}\)为旋转轴逆时针旋转了\(90^\circ\)。正如图9所示，\(\mathbf{v}\)分解为\(\mathbf{v}_\parallel\)和\(\mathbf{v}_\perp\)，用右手法则不难确定出\(\mathbf{k}\times\mathbf{v}\)的方向，进而不难发现，\(\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)可以看做将\(\mathbf{v}_\perp\)以\(\mathbf{k}\)为旋转轴逆时针旋转了\(180^\circ\)，图9中的(椭)圆正反映了\(\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)、\(\mathbf{k}\times\mathbf{v}\)、\(\mathbf{v}_\perp\)三者“大小相等”的关系。最终，可知\(\mathbf{v}_\perp=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)。
　　

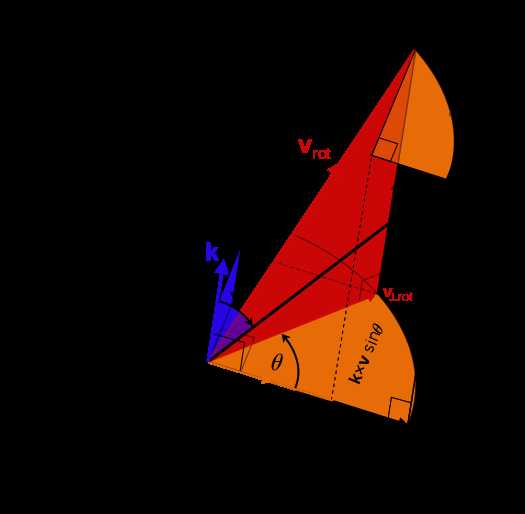
　　从图8还可以看出，v的平行分量\(\mathbf{v}_\parallel\)不会因为旋转而改变，旋转后的向量\(\mathbf{v}_{rot}\)的平行分量依然等于\(\mathbf{v}_\parallel\)，即\(\mathbf{v}_{\parallel rot}=\mathbf{v}_\parallel\)。
　　而v的正交分量\(\mathbf{v}_\perp\)在旋转过程中大小不变，方向会发生变化，即

\begin{equation} \begin{split} &|\mathbf{v}_{\perp rot}|=|\mathbf{v}_\perp|\&\mathbf{v}_{\perp rot}=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}_\perp=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

上述第2个等式通过图9可以得出，将圆看做\(xOy\)坐标系平面，\(\mathbf{v}_\perp\)所在的直线看做\(x\)轴，\(\mathbf{k}\times\mathbf{v}\)所在的直线看做\(y\)轴，结合三角函数，很容易用\(\mathbf{v}_\perp\)和\(\mathbf{k}\times\mathbf{v}\)表示出\(\mathbf{v}_\perp\)。

　　到这已经得出罗德里格斯公式了：

\begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\&=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\&=\mathbf{v}_\parallel+\cos\theta(\mathbf{v}-\mathbf{v}_\parallel)+\sin\theta\mathbf{k}\times\mathbf{v}\&=\cos\theta\mathbf{v}+(1-\cos\theta)\mathbf{v}_\parallel+\sin\theta\mathbf{k}\times\mathbf{v}\&=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

矩阵形式

　　在叉积部分提到过叉积可以表示为矩阵乘向量的形式，类似地，罗德里格斯旋转公式可以表示为旋转矩阵乘以向量的形式，\(\mathbf{v}_{rot}=\mathbf{R}\mathbf{v}\)，其中\(\mathbf{R}\)是旋转矩阵。在slam14讲\(^{[4]}\)中的表示如下：
\begin{equation}
\mathbf{R}=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{k}\mathbf{k}^T+\sin\theta\mathbf{k}^\wedge
\end{equation}
其中，\(\mathbf{I}\)表示单位矩阵，\(\mathbf{k}\)表示旋转向量（书中用\(\mathbf{n}\)表示旋转向量），\(\mathbf{k}^\wedge\)表示由\(\mathbf{k}\)得到的反对称矩阵。从式(13)不难看出上式，另外，结合式(13)还可以得到下面这个式子：

\begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\&=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\&=\mathbf{v}-\mathbf{v}_\perp+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\&=\mathbf{v}+(\sin\theta)\mathbf{k}\times\mathbf{v}+(1-\cos\theta)\mathbf{k}\times\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

从而，得出这个维基百科上的矩阵表示：

\begin{equation} \begin{split} \mathbf{v}_{rot}=\mathbf{R}\mathbf{v}=\mathbf{v}+(\sin\theta)\mathbf{K}\mathbf{v}+(1-\cos\theta)\mathbf{K}^2\mathbf{v} \end{split} \end{equation}

其中，\(\mathbf{R}=\mathbf{I}+(\sin\theta)\mathbf{K}+(1-\cos\theta)\mathbf{K}^2\)，\(\mathbf{K}\)表示由旋转向量\(\mathbf{k}\)生成的反对称矩阵。

参考：

[1] Rodrigues‘ rotation formula
[2] Cross product
[3] Vector projection
[4] 视觉SLAM十四讲：从理论到实践

罗德里格斯旋转公式（Rodrigues' rotation formula）推导

标签：空间   视觉   定义   法则   结合   mic   oss   lin   坐标轴   

原文地址：https://www.cnblogs.com/wtyuan/p/12324495.html