标签:actor fonts 不执行 enumerate point 缺失值 statistic reset 坐标
项目目的:利用车贷金融数据建立评分卡,并尝试多次迭代观察不同行为对模型,以及建模中间过程产生哪些影响。
首先是标准化导入需要使用的工具
import pandas as pd import numpy as np import matplotlib.pyplot as plt plt.style.use("ggplot")#风格设置 import seaborn as sns sns.set_style("whitegrid") %matplotlib inline import warnings #忽略错误模块 warnings.filterwarnings("ignore") plt.rcParams["font.sans-serif"]=["SimHei"] #指定默认字体
导入需要的数据
acc = pd.read_csv(‘accepts.csv‘) #通过的客户 rej = pd.read_csv(‘rejects.csv‘) #拒绝的客户
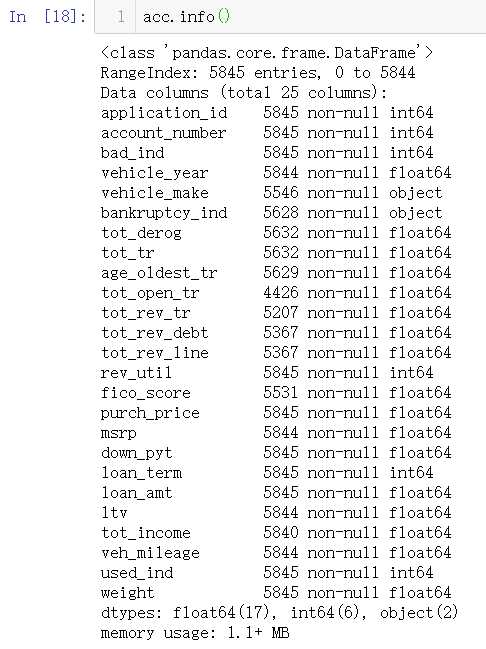
pd.set_option("display.max_columns",len(acc.columns))#解决全部显示的问题 acc.head()

各变量含义介绍: #中文含义
#中文含义
##application_id---申请者ID
##account_number---帐户号
##bad_ind---是否违约
##vehicle_year---汽车购买时间
##vehicle_make---汽车制造商
##bankruptcy_ind---曾经破产标识
##tot_derog---五年内信用不良事件数量(比如手机欠费消号)
##tot_tr---全部帐户数量
##age_oldest_tr---最久账号存续时间(月)
##tot_open_tr---在使用帐户数量
##tot_rev_tr---在使用可循环贷款帐户数量(比如信用卡)
##tot_rev_debt---在使用可循环贷款帐户余额(比如信用卡欠款)
##tot_rev_line---可循环贷款帐户限额(信用卡授权额度)
##rev_util---可循环贷款帐户使用比例(余额/限额)
##fico_score---FICO打分
##purch_price---汽车购买金额(元)
##msrp---建议售价
##down_pyt---分期付款的首次交款
##loan_term---贷款期限(月)
##loan_amt---贷款金额
##ltv---贷款金额/建议售价*100
##tot_income---月均收入(元)
##veh_mileage---行使历程(Mile)
##used_ind---是否使用
##weight---样本权重
数据清洗
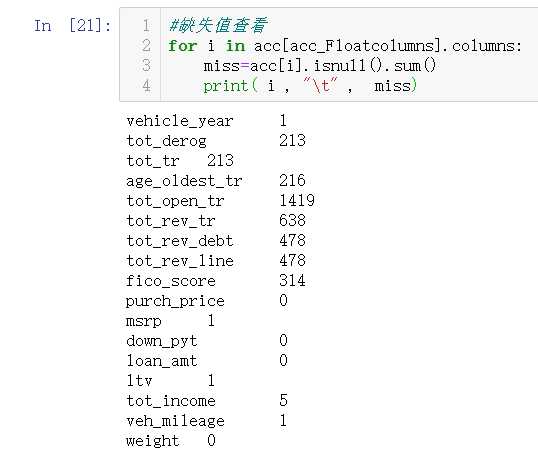
1.缺失值处理
数值数据处理
acc_Floatcolumns=[i for i in acc.columns if acc[i].dtype=="float"] rej_Floatcolumns=[i for i in rej.columns if rej[i].dtype=="float"]
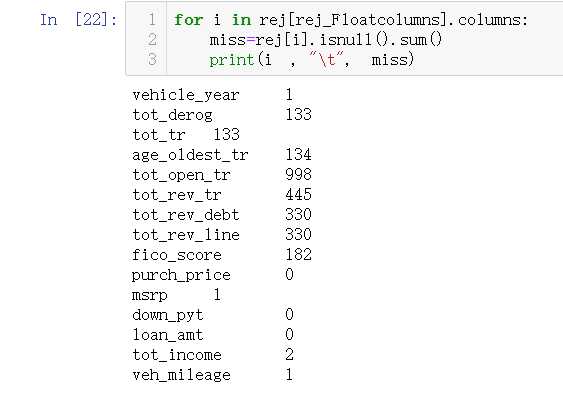
利用Imputer 模块进行缺失值填充

from sklearn.preprocessing import Imputer#只支持 均值,中位数,众数填补 inputer = Imputer(missing_values = ‘NaN‘, strategy = ‘mean‘, axis = 0) inputer = inputer.fit(X) X = inputer.transform(X) 主要参数说明: missing_values:缺失值,可以为整数或NaN(缺失值numpy.nan用字符串‘NaN’表示),默认为NaN strategy:替换策略,字符串,默认用均值‘mean’替换 ①若为mean时,用特征列的均值替换 ②若为median时,用特征列的中位数替换 ③若为most_frequent时,用特征列的众数替换 axis:指定轴数,默认axis=0代表列,axis=1代表行 copy:设置为True代表不在原数据集上修改,设置为False时,就地修改,存在如下情况时,即使设置为False时,也不会就地修改 ①X不是浮点值数组 ②X是稀疏且missing_values=0 ③axis=0且X为CRS矩阵 ④axis=1且X为CSC矩阵 statistics_属性:axis设置为0时,每个特征的填充值数组,axis=1时,报没有该属性错误
from sklearn.preprocessing import Imputer
#数值信息缺失值处理 inputer=Imputer(missing_values=‘NaN‘, strategy=‘mean‘, axis=0) #均值填充,列 inputer=inputer.fit(acc[acc_Floatcolumns])# 计算 acc[acc_Floatcolumns] = inputer.transform(acc[acc_Floatcolumns]) #引用
inputer=Imputer(missing_values=‘NaN‘, strategy=‘mean‘, axis=0) #均值填充,列 inputer=inputer.fit(rej[rej_Floatcolumns])# 计算 rej[rej_Floatcolumns] = inputer.transform(rej[rej_Floatcolumns]) #引用

for i in rej_Floatcolumns: rej[i]=acc[i].fillna(rej[i].mean()) #mean()均值 #mode()众数 #median()中位数
数值型数据缺失值填充完毕
#分类信息缺失值数据处理 acc_objectcolumns=[i for i in acc.columns if acc[i].dtype=="object"] rej_objectcolumns=[i for i in rej.columns if rej[i].dtype=="object"]
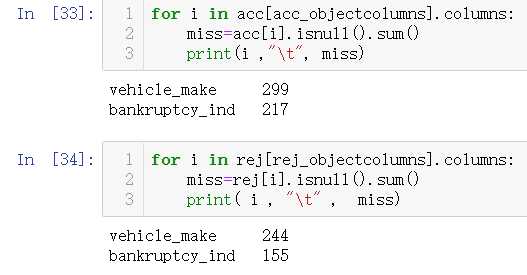
两个数据为汽车制造商与曾经破产标志,这里删除汽车制造商。
#删除汽车制造商特征 acc.drop(columns="vehicle_make",axis=0,inplace=True) rej.drop(columns="vehicle_make",axis=0,inplace=True)
对于破产可以单独一类归纳,但在这里占比实在太小,没太大意义,所以直接替换成N代替
#空值替换成N acc["bankruptcy_ind"]=acc["bankruptcy_ind"].fillna("N") rej["bankruptcy_ind"]=rej["bankruptcy_ind"].fillna("N")

同值信息处理:
一般如果某一项特征超过90%都是同一种信息,那么一般对模型将毫无作用,所以优先删除这一变量。
#同值信息处理 from scipy.stats import mode equ_fea=[] for i in acc.columns: mode_value=mode(acc[i])[0][0] #求众数值 mode_rate=mode(acc[i])[1][0]/acc.shape[0]#求得众数占比 if mode_rate >0.9: equ_fea.append([i,mode_value,mode_rate]) dt=pd.DataFrame(equ_fea,columns=["name","value","equi"]) dt.sort_values(by="equi")

删除处理
acc.drop(columns="bankruptcy_ind",axis=0,inplace=True) rej.drop(columns="bankruptcy_ind",axis=0,inplace=True)
#借款期限描述 cla=["loan_term"] for i in cla: pvt=pd.pivot_table(acc[["bad_ind",i]],index=i,columns="bad_ind",aggfunc=len) pvt.plot(kind="bar")
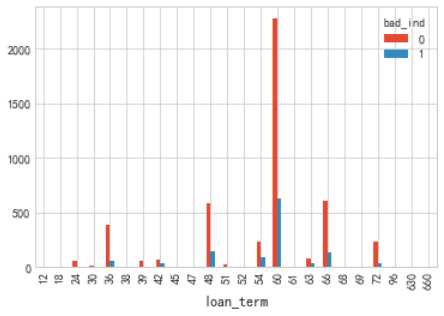
借款期限分布符合一般规律,逾期比列方面没有太大区别
cel=[i for i in acc.columns if acc[i].dtypes =="float"] for i ,j in enumerate(cel): plt.figure(figsize=(8,5*len(cel))) plt.subplot(len(cel),1,i+1) sns.distplot(acc[j][acc.bad_ind==0],color="b") sns.distplot(acc[j][acc.bad_ind==1],color="r")
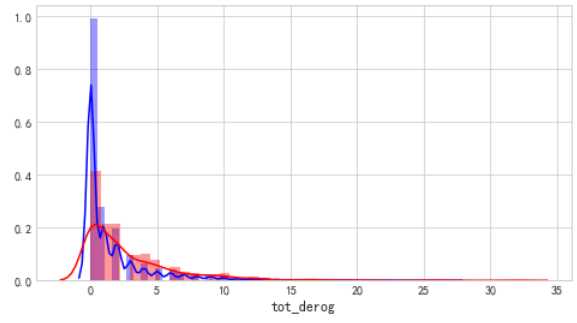
具备不良信息的客户,占比接近40%,次数越多,相对的逾期客户越多
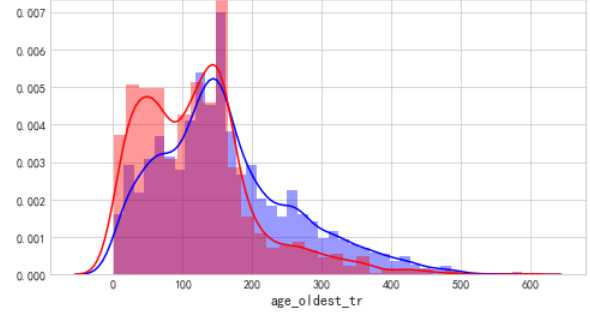
从账龄来看,账龄越短,逾期人数越多,逾期概率也越高
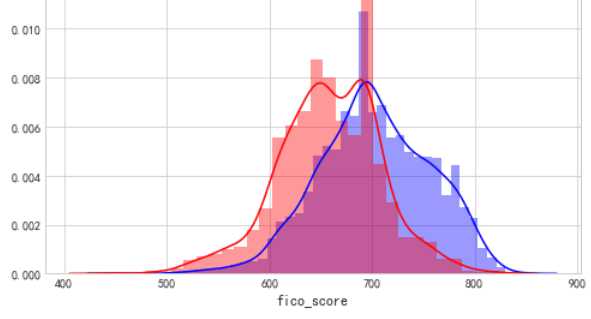
FICO评分,呈现正太分布,并且能够看见,评分越低逾期率越高,700分为分界,得分越高逾期率越低,评分效果是比较显著的
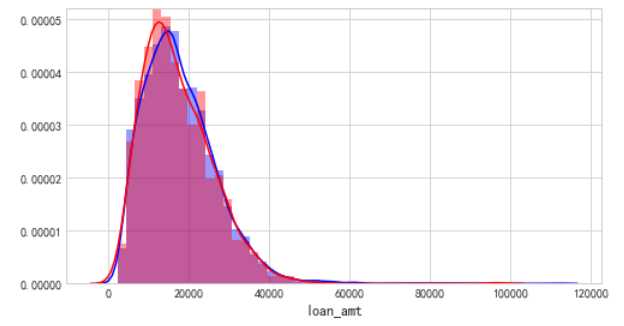
借款金额多集中在4万一下,呈现正太分布
拒绝推断
#一般情况下如果我们只拿申请通过的样本建立评分卡,会出现样本偏差,不能很好适用于整个申请人群,同时也方便评分卡覆盖之前的决策影响。
#这里采用K-NN做拒绝推断
1.取出部分变量用于做KNN:由于KNN算法要求使用连续变量,因此仅选了部分重要的连续变量用于做KNN模型
acc_x = acc[["tot_derog","age_oldest_tr","rev_util","fico_score","ltv"]] acc_y = acc[‘bad_ind‘] rej_x = rej[["tot_derog","age_oldest_tr","rev_util","fico_score","ltv"]]
#数据标准化 def MaxMinNormalization(dataset): maxdf=dataset.max() mindf=dataset.min() normal=(dataset-mindf) / (maxdf-mindf) return normal
acc_x_norm =MaxMinNormalization(acc_x)
rej_x_norm =MaxMinNormalization(rej_x)
#利用knn模型进行预测,做拒绝推断 from sklearn.neighbors import NearestNeighbors from sklearn.neighbors import KNeighborsClassifier neigh = KNeighborsClassifier(n_neighbors=5, weights=‘distance‘) neigh.fit(acc_x_norm, acc_y)

rej[‘bad_ind‘] = neigh.predict(rej_x_norm)
#删除ID rej.drop(columns="application_id",axis=0,inplace=True)
#将审核通过的申请者和未通过的申请者进行合并
# accepts的数据是针对于违约用户的过度抽样
#因此,rejects也要进行同样比例的抽样
rej_res = rej[rej[‘bad_ind‘] == 0].sample(1340) rej_res = pd.concat([rej_res, rej[rej[‘bad_ind‘] == 1]], axis = 0) data = pd.concat([acc, rej_res], axis=0)
建模数据准备
#盖帽法处理年份变量中的异常值,并将年份其转化为距现在多长时间 year_min = data.vehicle_year.quantile(0.1) #求得分位数 year_max = data.vehicle_year.quantile(0.99) data.vehicle_year = data.vehicle_year.map(lambda x: year_min if x <= year_min else x) data.vehicle_year = data.vehicle_year.map(lambda x: year_max if x >= year_max else x) data.vehicle_year = data.vehicle_year.map(lambda x: 2019 - x)
#盖帽法处理所有数值型数据的异常值 dist=["age_oldest_tr","down_pyt","fico_score","loan_amt","loan_term","ltv","msrp","purch_price", "rev_util","tot_income","tot_rev_debt","tot_rev_line","tot_tr","veh_mileage"] for i in dist: i_min=data[i].quantile(0.1) i_max=data[i].quantile(0.99) data[i]=data[i].map(lambda x : i_min if x <= i_min else x) data[i]=data[i].map(lambda x : i_max if x >= i_max else x)
#划分 x与y x_list=list(data.columns) x_list.remove("bad_ind") #再x_list中剔除 bad_ind 变量 x=data[x_list] y=data["bad_ind"]
#利用随机森林选择GINI系数排名靠前的变量 from sklearn.ensemble import RandomForestClassifier clf = RandomForestClassifier(max_depth=5, random_state=0) clf.fit(x,y)

#返回变量的GINI系数 clf.feature_importances_

#选择排名前9的特征 importances = list(clf.feature_importances_) importances_order = importances.copy() importances_order.sort(reverse=True) cols = list(x.columns) col_top = [] for i in importances_order[:9]: col_top.append((i,cols[importances.index(i)])) col_top

#截取columns col=[i[1] for i in col_top] col

#开始进行特征分箱 import numpy as np import pandas as pd from sklearn.metrics import confusion_matrix
1.卡方分箱

def SplitData(df, col, numOfSplit, special_attribute=[]): ‘‘‘ :param df: 按照col排序后的数据集 :param col: 待分箱的变量 :param numOfSplit: 切分的组别数 :param special_attribute: 在切分数据集的时候,某些特殊值需要排除在外 :return: 在原数据集上增加一列,把原始细粒度的col重新划分成粗粒度的值,便于分箱中的合并处理 ‘‘‘ df2 = df.copy() if special_attribute != []: df2 = df.loc[~df[col].isin(special_attribute)] N = df2.shape[0] n = int(N/numOfSplit) splitPointIndex = [i*n for i in range(1,numOfSplit)] rawValues = sorted(list(df2[col])) splitPoint = [rawValues[i] for i in splitPointIndex] splitPoint = sorted(list(set(splitPoint))) return splitPoint def MaximumBinPcnt(df,col): ‘‘‘ :return: 数据集df中,变量col的分布占比 ‘‘‘ N = df.shape[0] total = df.groupby([col])[col].count() pcnt = total*1.0/N return max(pcnt)

def Chi2(df, total_col, bad_col): ‘‘‘ :param df: 包含全部样本总计与坏样本总计的数据框 :param total_col: 全部样本的个数 :param bad_col: 坏样本的个数 :return: 卡方值 ‘‘‘ df2 = df.copy() # 求出df中,总体的坏样本率和好样本率 badRate = sum(df2[bad_col])*1.0/sum(df2[total_col]) # 当全部样本只有好或者坏样本时,卡方值为0 if badRate in [0,1]: return 0 df2[‘good‘] = df2.apply(lambda x: x[total_col] - x[bad_col], axis = 1) goodRate = sum(df2[‘good‘]) * 1.0 / sum(df2[total_col]) # 期望坏(好)样本个数=全部样本个数*平均坏(好)样本占比 df2[‘badExpected‘] = df[total_col].apply(lambda x: x*badRate) df2[‘goodExpected‘] = df[total_col].apply(lambda x: x * goodRate) badCombined = zip(df2[‘badExpected‘], df2[bad_col]) goodCombined = zip(df2[‘goodExpected‘], df2[‘good‘]) badChi = [(i[0]-i[1])**2/i[0] for i in badCombined] goodChi = [(i[0] - i[1]) ** 2 / i[0] for i in goodCombined] chi2 = sum(badChi) + sum(goodChi) return chi2 def BinBadRate(df, col, target, grantRateIndicator=0): ‘‘‘ :param df: 需要计算好坏比率的数据集 :param col: 需要计算好坏比率的特征 :param target: 好坏标签 :param grantRateIndicator: 1返回总体的坏样本率,0不返回 :return: 每箱的坏样本率,以及总体的坏样本率(当grantRateIndicator==1时) ‘‘‘ total = df.groupby([col])[target].count() total = pd.DataFrame({‘total‘: total}) bad = df.groupby([col])[target].sum() bad = pd.DataFrame({‘bad‘: bad}) regroup = total.merge(bad, left_index=True, right_index=True, how=‘left‘) regroup.reset_index(level=0, inplace=True) regroup[‘bad_rate‘] = regroup.apply(lambda x: x.bad / x.total, axis=1) dicts = dict(zip(regroup[col],regroup[‘bad_rate‘])) if grantRateIndicator==0: return (dicts, regroup) N = sum(regroup[‘total‘]) B = sum(regroup[‘bad‘]) overallRate = B * 1.0 / N return (dicts, regroup, overallRate) def AssignGroup(x, bin): ‘‘‘ :return: 数值x在区间映射下的结果。例如,x=2,bin=[0,3,5], 由于0<x<3,x映射成3 ‘‘‘ N = len(bin) if x<=min(bin): return min(bin) elif x>max(bin): return 10e10 else: for i in range(N-1): if bin[i] < x <= bin[i+1]: return bin[i+1] def AssignBin(x, cutOffPoints,special_attribute=[]): ‘‘‘ :param x: 某个变量的某个取值 :param cutOffPoints: 上述变量的分箱结果,用切分点表示 :param special_attribute: 不参与分箱的特殊取值 :return: 分箱后的对应的第几个箱,从0开始 例如, cutOffPoints = [10,20,30], 对于 x = 7, 返回 Bin 0;对于x=23,返回Bin 2; 对于x = 35, return Bin 3。 对于特殊值,返回的序列数前加"-" ‘‘‘ cutOffPoints2 = [i for i in cutOffPoints if i not in special_attribute] numBin = len(cutOffPoints2) if x in special_attribute: i = special_attribute.index(x)+1 return ‘Bin {}‘.format(0-i) if x<=cutOffPoints2[0]: return ‘Bin 0‘ elif x > cutOffPoints2[-1]: return ‘Bin {}‘.format(numBin) else: for i in range(0,numBin): if cutOffPoints2[i] < x <= cutOffPoints2[i+1]: return ‘Bin {}‘.format(i+1)

def ChiMerge(df, col, target, max_interval=5,special_attribute=[],minBinPcnt=0): ‘‘‘ :param df: 包含目标变量与分箱属性的数据框 :param col: 需要分箱的属性 :param target: 目标变量,取值0或1 :param max_interval: 最大分箱数。如果原始属性的取值个数低于该参数,不执行这段函数 :param special_attribute: 不参与分箱的属性取值 :param minBinPcnt:最小箱的占比,默认为0 :return: 分箱结果 ‘‘‘ colLevels = sorted(list(set(df[col]))) N_distinct = len(colLevels) if N_distinct <= max_interval: #如果原始属性的取值个数低于max_interval,不执行这段函数 print("The number of original levels for {} is less than or equal to max intervals".format(col)) return colLevels[:-1] else: if len(special_attribute)>=1: df1 = df.loc[df[col].isin(special_attribute)] df2 = df.loc[~df[col].isin(special_attribute)] else: df2 = df.copy() N_distinct = len(list(set(df2[col]))) # 步骤一: 通过col对数据集进行分组,求出每组的总样本数与坏样本数 if N_distinct > 100: split_x = SplitData(df2, col, 100) df2[‘temp‘] = df2[col].map(lambda x: AssignGroup(x, split_x)) else: df2[‘temp‘] = df2[col] # 总体bad rate将被用来计算expected bad count (binBadRate, regroup, overallRate) = BinBadRate(df2, ‘temp‘, target, grantRateIndicator=1) # 首先,每个单独的属性值将被分为单独的一组 # 对属性值进行排序,然后两两组别进行合并 colLevels = sorted(list(set(df2[‘temp‘]))) groupIntervals = [[i] for i in colLevels] # 步骤二:建立循环,不断合并最优的相邻两个组别,直到: # 1,最终分裂出来的分箱数<=预设的最大分箱数 # 2,每箱的占比不低于预设值(可选) # 3,每箱同时包含好坏样本 # 如果有特殊属性,那么最终分裂出来的分箱数=预设的最大分箱数-特殊属性的个数 split_intervals = max_interval - len(special_attribute) while (len(groupIntervals) > split_intervals): # 终止条件: 当前分箱数=预设的分箱数 # 每次循环时, 计算合并相邻组别后的卡方值。具有最小卡方值的合并方案,是最优方案 chisqList = [] for k in range(len(groupIntervals)-1): temp_group = groupIntervals[k] + groupIntervals[k+1] df2b = regroup.loc[regroup[‘temp‘].isin(temp_group)] chisq = Chi2(df2b, ‘total‘, ‘bad‘) chisqList.append(chisq) best_comnbined = chisqList.index(min(chisqList)) groupIntervals[best_comnbined] = groupIntervals[best_comnbined] + groupIntervals[best_comnbined+1] # 当将最优的相邻的两个变量合并在一起后,需要从原来的列表中将其移除。例如,将[3,4,5] 与[6,7]合并成[3,4,5,6,7]后,需要将[3,4,5] 与[6,7]移除,保留[3,4,5,6,7] groupIntervals.remove(groupIntervals[best_comnbined+1]) groupIntervals = [sorted(i) for i in groupIntervals] cutOffPoints = [max(i) for i in groupIntervals[:-1]] # 检查是否有箱没有好或者坏样本。如果有,需要跟相邻的箱进行合并,直到每箱同时包含好坏样本 groupedvalues = df2[‘temp‘].apply(lambda x: AssignBin(x, cutOffPoints)) df2[‘temp_Bin‘] = groupedvalues (binBadRate,regroup) = BinBadRate(df2, ‘temp_Bin‘, target) [minBadRate, maxBadRate] = [min(binBadRate.values()),max(binBadRate.values())] while minBadRate ==0 or maxBadRate == 1: # 找出全部为好/坏样本的箱 indexForBad01 = regroup[regroup[‘bad_rate‘].isin([0,1])].temp_Bin.tolist() bin=indexForBad01[0] # 如果是最后一箱,则需要和上一个箱进行合并,也就意味着分裂点cutOffPoints中的最后一个需要移除 if bin == max(regroup.temp_Bin): cutOffPoints = cutOffPoints[:-1] # 如果是第一箱,则需要和下一个箱进行合并,也就意味着分裂点cutOffPoints中的第一个需要移除 elif bin == min(regroup.temp_Bin): cutOffPoints = cutOffPoints[1:] # 如果是中间的某一箱,则需要和前后中的一个箱进行合并,依据是较小的卡方值 else: # 和前一箱进行合并,并且计算卡方值 currentIndex = list(regroup.temp_Bin).index(bin) prevIndex = list(regroup.temp_Bin)[currentIndex - 1] df3 = df2.loc[df2[‘temp_Bin‘].isin([prevIndex, bin])] (binBadRate, df2b) = BinBadRate(df3, ‘temp_Bin‘, target) chisq1 = Chi2(df2b, ‘total‘, ‘bad‘) # 和后一箱进行合并,并且计算卡方值 laterIndex = list(regroup.temp_Bin)[currentIndex + 1] df3b = df2.loc[df2[‘temp_Bin‘].isin([laterIndex, bin])] (binBadRate, df2b) = BinBadRate(df3b, ‘temp_Bin‘, target) chisq2 = Chi2(df2b, ‘total‘, ‘bad‘) if chisq1 < chisq2: cutOffPoints.remove(cutOffPoints[currentIndex - 1]) else: cutOffPoints.remove(cutOffPoints[currentIndex]) # 完成合并之后,需要再次计算新的分箱准则下,每箱是否同时包含好坏样本 groupedvalues = df2[‘temp‘].apply(lambda x: AssignBin(x, cutOffPoints)) df2[‘temp_Bin‘] = groupedvalues (binBadRate, regroup) = BinBadRate(df2, ‘temp_Bin‘, target) [minBadRate, maxBadRate] = [min(binBadRate.values()), max(binBadRate.values())] # 需要检查分箱后的最小占比 if minBinPcnt > 0: groupedvalues = df2[‘temp‘].apply(lambda x: AssignBin(x, cutOffPoints)) df2[‘temp_Bin‘] = groupedvalues valueCounts = groupedvalues.value_counts().to_frame() N = sum(valueCounts[‘temp‘]) valueCounts[‘pcnt‘] = valueCounts[‘temp‘].apply(lambda x: x * 1.0 / N) valueCounts = valueCounts.sort_index() minPcnt = min(valueCounts[‘pcnt‘]) while minPcnt < minBinPcnt and len(cutOffPoints) > 2: # 找出占比最小的箱 indexForMinPcnt = valueCounts[valueCounts[‘pcnt‘] == minPcnt].index.tolist()[0] # 如果占比最小的箱是最后一箱,则需要和上一个箱进行合并,也就意味着分裂点cutOffPoints中的最后一个需要移除 if indexForMinPcnt == max(valueCounts.index): cutOffPoints = cutOffPoints[:-1] # 如果占比最小的箱是第一箱,则需要和下一个箱进行合并,也就意味着分裂点cutOffPoints中的第一个需要移除 elif indexForMinPcnt == min(valueCounts.index): cutOffPoints = cutOffPoints[1:] # 如果占比最小的箱是中间的某一箱,则需要和前后中的一个箱进行合并,依据是较小的卡方值 else: # 和前一箱进行合并,并且计算卡方值 currentIndex = list(valueCounts.index).index(indexForMinPcnt) prevIndex = list(valueCounts.index)[currentIndex - 1] df3 = df2.loc[df2[‘temp_Bin‘].isin([prevIndex, indexForMinPcnt])] (binBadRate, df2b) = BinBadRate(df3, ‘temp_Bin‘, target) chisq1 = Chi2(df2b, ‘total‘, ‘bad‘) # 和后一箱进行合并,并且计算卡方值 laterIndex = list(valueCounts.index)[currentIndex + 1] df3b = df2.loc[df2[‘temp_Bin‘].isin([laterIndex, indexForMinPcnt])] (binBadRate, df2b) = BinBadRate(df3b, ‘temp_Bin‘, target) chisq2 = Chi2(df2b, ‘total‘, ‘bad‘) if chisq1 < chisq2: cutOffPoints.remove(cutOffPoints[currentIndex - 1]) else: cutOffPoints.remove(cutOffPoints[currentIndex]) groupedvalues = df2[‘temp‘].apply(lambda x: AssignBin(x, cutOffPoints)) df2[‘temp_Bin‘] = groupedvalues valueCounts = groupedvalues.value_counts().to_frame() valueCounts[‘pcnt‘] = valueCounts[‘temp‘].apply(lambda x: x * 1.0 / N) valueCounts = valueCounts.sort_index() minPcnt = min(valueCounts[‘pcnt‘]) cutOffPoints = special_attribute + cutOffPoints return cutOffPoints
def ChiMerge(df, col, target, max_interval=5,special_attribute=[],minBinPcnt=0): ‘‘‘ :param df: 包含目标变量与分箱属性的数据框 :param col: 需要分箱的属性 :param target: 目标变量,取值0或1 :param max_interval: 最大分箱数。如果原始属性的取值个数低于该参数,不执行这段函数 :param special_attribute: 不参与分箱的属性取值 :param minBinPcnt:最小箱的占比,默认为0 :return: 分箱结果
分别采用最小箱占比 0 和 0.5 进行两次分箱方便后续对比结果
#最小箱占比0 df_dist={} for i in col: df_feat=ChiMerge(data,i, "bad_ind", max_interval=5,special_attribute=[],minBinPcnt=0) df_dist[i]=df_feat print (df_dist)

#最小箱占比0.5 df_dist={} for i in col: df_feat=ChiMerge(data,i, "bad_ind", max_interval=5,special_attribute=[],minBinPcnt=0.5) df_dist[i]=df_feat print (df_dist)

#采用pd.cut()划分数据 def box_col_to_df(to_box,col,num_b):#数据集 需要转换的数据列 切割点LISI bins=[-100.0]+num_b+[1000000000.0] #因为pd.cut()是封闭的,这里把bins的上下区间扩大 to_box[col]=pd.cut(to_box[col],bins=bins,include_lowest=True,labels=range(len(bins)-1))
df=data[col] for i in col: box_col_to_df(df,i,df_dist[i])
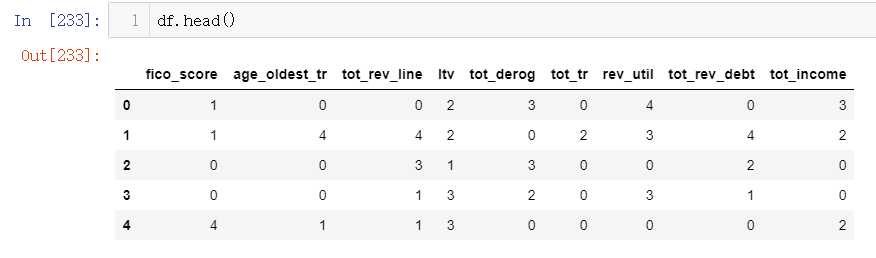
df2=data[col] for i in col: box_col_to_df(df2,i,df_dist[i])
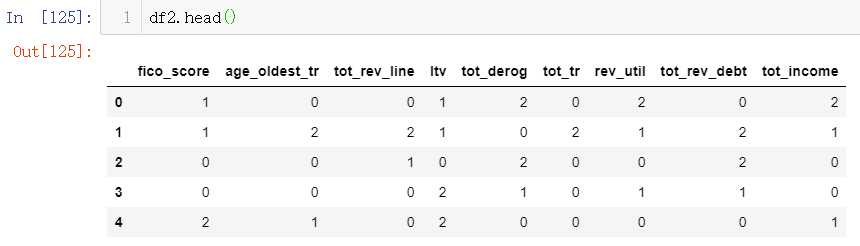

#计算woe 和IV 值 def CalcWOE(df, col, target): ‘‘‘ :param df: 包含需要计算WOE的变量和目标变量 :param col: 需要计算WOE、IV的变量,必须是分箱后的变量,或者不需要分箱的类别型变量 :param target: 目标变量,0、1表示好、坏 :return: 返回WOE和IV ‘‘‘ total = df.groupby([col])[target].count() total = pd.DataFrame({‘total‘: total}) bad = df.groupby([col])[target].sum() bad = pd.DataFrame({‘bad‘: bad}) regroup = total.merge(bad, left_index=True, right_index=True, how=‘left‘) regroup.reset_index(level=0, inplace=True) N = sum(regroup[‘total‘]) B = sum(regroup[‘bad‘]) regroup[‘good‘] = regroup[‘total‘] - regroup[‘bad‘] G = N - B regroup[‘bad_pcnt‘] = regroup[‘bad‘].map(lambda x: x*1.0/B) regroup[‘good_pcnt‘] = regroup[‘good‘].map(lambda x: x * 1.0 / G) regroup[‘WOE‘] = regroup.apply(lambda x: np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1) WOE_dict = regroup[[col,‘WOE‘]].set_index(col).to_dict(orient=‘index‘) for k, v in WOE_dict.items(): WOE_dict[k] = v[‘WOE‘] IV = regroup.apply(lambda x: (x.good_pcnt-x.bad_pcnt)*np.log(x.good_pcnt*1.0/x.bad_pcnt),axis = 1) IV = sum(IV) return {"WOE": WOE_dict, ‘IV‘:IV}
df["bad_ind"]=data["bad_ind"] df2["bad_ind"]=data["bad_ind"]
iv=[] IV={} WOE={} for i in col: df_dist=CalcWOE(df, i, "bad_ind") IV[i]=df_dist["IV"] iv.append([i,df_dist["IV"]]) WOE[i]=df_dist["WOE"] lis=pd.DataFrame(iv,columns=["name","iv"]) print(IV) print(WOE) print(lis

iv=[] IV={} WOE={} for i in col: df_dist=CalcWOE(df2, i, "bad_ind") IV[i]=df_dist["IV"] iv.append([i,df_dist["IV"]]) WOE[i]=df_dist["WOE"] lis=pd.DataFrame(iv,columns=["name","iv"]) print(IV) print(WOE) print(lis)
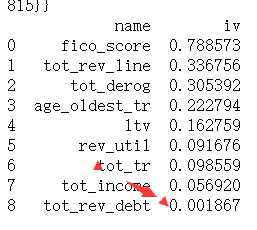
可见分箱方案的选择对IV值存在较直接的影响,实际操作中需要结合实际经验不断迭代。

‘‘‘ :return: 返回序列x中有几个元素不满足单调性,以及这些元素的位置。 例如,x=[1,3,2,5], 元素3比前后两个元素都大,不满足单调性;元素2比前后两个元素都小,也不满足单调性。 故返回的不满足单调性的元素个数为2,位置为1和2. ‘‘‘ monotone = [x[i]<x[i+1] and x[i] < x[i-1] or x[i]>x[i+1] and x[i] > x[i-1] for i in range(1,len(x)-1)] index_of_nonmonotone = [i+1 for i in range(len(monotone)) if monotone[i]] return {‘count_of_nonmonotone‘:monotone.count(True), ‘index_of_nonmonotone‘:index_of_nonmonotone} ## 判断某变量的坏样本率是否单调 def BadRateMonotone(df, sortByVar, target,special_attribute = []): ‘‘‘ :param df: 包含检验坏样本率的变量,和目标变量 :param sortByVar: 需要检验坏样本率的变量 :param target: 目标变量,0、1表示好、坏 :param special_attribute: 不参与检验的特殊值 :return: 坏样本率单调与否 ‘‘‘ df2 = df.loc[~df[sortByVar].isin(special_attribute)] if len(set(df2[sortByVar])) <= 2: return True regroup = BinBadRate(df2, sortByVar, target)[1] combined = zip(regroup[‘total‘],regroup[‘bad‘]) badRate = [x[1]*1.0/x[0] for x in combined] badRateNotMonotone = FeatureMonotone(badRate)[‘count_of_nonmonotone‘] if badRateNotMonotone > 0: return False else: return True

def MergeBad0(df,col,target, direction=‘bad‘): ‘‘‘ :param df: 包含检验0%或者100%坏样本率 :param col: 分箱后的变量或者类别型变量。检验其中是否有一组或者多组没有坏样本或者没有好样本。如果是, 则需要进行合并 :param target: 目标变量,0、1表示好、坏 :return: 合并方案,使得每个组里同时包含好坏样本 ‘‘‘ regroup = BinBadRate(df, col, target)[1] if direction == ‘bad‘: # 如果是合并0坏样本率的组,则跟最小的非0坏样本率的组进行合并 regroup = regroup.sort_values(by = ‘bad_rate‘) else: # 如果是合并0好样本率的组,则跟最小的非0好样本率的组进行合并 regroup = regroup.sort_values(by=‘bad_rate‘,ascending=False) regroup.index = range(regroup.shape[0]) col_regroup = [[i] for i in regroup[col]] del_index = [] for i in range(regroup.shape[0]-1): col_regroup[i+1] = col_regroup[i] + col_regroup[i+1] del_index.append(i) if direction == ‘bad‘: if regroup[‘bad_rate‘][i+1] > 0: break else: if regroup[‘bad_rate‘][i+1] < 1: break col_regroup2 = [col_regroup[i] for i in range(len(col_regroup)) if i not in del_index] newGroup = {} for i in range(len(col_regroup2)): for g2 in col_regroup2[i]: newGroup[g2] = ‘Bin ‘+str(i) return newGroup

def Monotone_Merge(df, target, col): ‘‘‘ :return:将数据集df中,不满足坏样本率单调性的变量col进行合并,使得合并后的新的变量中,坏样本率单调,输出合并方案。 例如,col=[Bin 0, Bin 1, Bin 2, Bin 3, Bin 4]是不满足坏样本率单调性的。合并后的col是: [Bin 0&Bin 1, Bin 2, Bin 3, Bin 4]. 合并只能在相邻的箱中进行。 迭代地寻找最优合并方案。每一步迭代时,都尝试将所有非单调的箱进行合并,每一次尝试的合并都是跟前后箱进行合并再做比较 ‘‘‘ def MergeMatrix(m, i,j,k): ‘‘‘ :param m: 需要合并行的矩阵 :param i,j: 合并第i和j行 :param k: 删除第k行 :return: 合并后的矩阵 ‘‘‘ m[i, :] = m[i, :] + m[j, :] m = np.delete(m, k, axis=0) return m def Merge_adjacent_Rows(i, bad_by_bin_current, bins_list_current, not_monotone_count_current): ‘‘‘ :param i: 需要将第i行与前、后的行分别进行合并,比较哪种合并方案最佳。判断准则是,合并后非单调性程度减轻,且更加均匀 :param bad_by_bin_current:合并前的分箱矩阵,包括每一箱的样本个数、坏样本个数和坏样本率 :param bins_list_current: 合并前的分箱方案 :param not_monotone_count_current:合并前的非单调性元素个数 :return:分箱后的分箱矩阵、分箱方案、非单调性元素个数和衡量均匀性的指标balance ‘‘‘ i_prev = i - 1 i_next = i + 1 bins_list = bins_list_current.copy() bad_by_bin = bad_by_bin_current.copy() not_monotone_count = not_monotone_count_current #合并方案a:将第i箱与前一箱进行合并 bad_by_bin2a = MergeMatrix(bad_by_bin.copy(), i_prev, i, i) bad_by_bin2a[i_prev, -1] = bad_by_bin2a[i_prev, -2] / bad_by_bin2a[i_prev, -3] not_monotone_count2a = FeatureMonotone(bad_by_bin2a[:, -1])[‘count_of_nonmonotone‘] # 合并方案b:将第i行与后一行进行合并 bad_by_bin2b = MergeMatrix(bad_by_bin.copy(), i, i_next, i_next) bad_by_bin2b[i, -1] = bad_by_bin2b[i, -2] / bad_by_bin2b[i, -3] not_monotone_count2b = FeatureMonotone(bad_by_bin2b[:, -1])[‘count_of_nonmonotone‘] balance = ((bad_by_bin[:, 1] / N).T * (bad_by_bin[:, 1] / N))[0, 0] balance_a = ((bad_by_bin2a[:, 1] / N).T * (bad_by_bin2a[:, 1] / N))[0, 0] balance_b = ((bad_by_bin2b[:, 1] / N).T * (bad_by_bin2b[:, 1] / N))[0, 0] #满足下述2种情况时返回方案a:(1)方案a能减轻非单调性而方案b不能;(2)方案a和b都能减轻非单调性,但是方案a的样本均匀性优于方案b if not_monotone_count2a < not_monotone_count_current and not_monotone_count2b >= not_monotone_count_current or not_monotone_count2a < not_monotone_count_current and not_monotone_count2b < not_monotone_count_current and balance_a < balance_b: bins_list[i_prev] = bins_list[i_prev] + bins_list[i] bins_list.remove(bins_list[i]) bad_by_bin = bad_by_bin2a not_monotone_count = not_monotone_count2a balance = balance_a # 同样地,满足下述2种情况时返回方案b:(1)方案b能减轻非单调性而方案a不能;(2)方案a和b都能减轻非单调性,但是方案b的样本均匀性优于方案a elif not_monotone_count2a >= not_monotone_count_current and not_monotone_count2b < not_monotone_count_current or not_monotone_count2a < not_monotone_count_current and not_monotone_count2b < not_monotone_count_current and balance_a > balance_b: bins_list[i] = bins_list[i] + bins_list[i_next] bins_list.remove(bins_list[i_next]) bad_by_bin = bad_by_bin2b not_monotone_count = not_monotone_count2b balance = balance_b #如果方案a和b都不能减轻非单调性,返回均匀性更优的合并方案 else: if balance_a< balance_b: bins_list[i] = bins_list[i] + bins_list[i_next] bins_list.remove(bins_list[i_next]) bad_by_bin = bad_by_bin2b not_monotone_count = not_monotone_count2b balance = balance_b else: bins_list[i] = bins_list[i] + bins_list[i_next] bins_list.remove(bins_list[i_next]) bad_by_bin = bad_by_bin2b not_monotone_count = not_monotone_count2b balance = balance_b return {‘bins_list‘: bins_list, ‘bad_by_bin‘: bad_by_bin, ‘not_monotone_count‘: not_monotone_count, ‘balance‘: balance} N = df.shape[0] [badrate_bin, bad_by_bin] = BinBadRate(df, col, target) bins = list(bad_by_bin[col]) bins_list = [[i] for i in bins] badRate = sorted(badrate_bin.items(), key=lambda x: x[0]) badRate = [i[1] for i in badRate] not_monotone_count, not_monotone_position = FeatureMonotone(badRate)[‘count_of_nonmonotone‘], FeatureMonotone(badRate)[‘index_of_nonmonotone‘] #迭代地寻找最优合并方案,终止条件是:当前的坏样本率已经单调,或者当前只有2箱 while (not_monotone_count > 0 and len(bins_list)>2): #当非单调的箱的个数超过1个时,每一次迭代中都尝试每一个箱的最优合并方案 all_possible_merging = [] for i in not_monotone_position: merge_adjacent_rows = Merge_adjacent_Rows(i, np.mat(bad_by_bin), bins_list, not_monotone_count) all_possible_merging.append(merge_adjacent_rows) balance_list = [i[‘balance‘] for i in all_possible_merging] not_monotone_count_new = [i[‘not_monotone_count‘] for i in all_possible_merging] #如果所有的合并方案都不能减轻当前的非单调性,就选择更加均匀的合并方案 if min(not_monotone_count_new) >= not_monotone_count: best_merging_position = balance_list.index(min(balance_list)) #如果有多个合并方案都能减轻当前的非单调性,也选择更加均匀的合并方案 else: better_merging_index = [i for i in range(len(not_monotone_count_new)) if not_monotone_count_new[i] < not_monotone_count] better_balance = [balance_list[i] for i in better_merging_index] best_balance_index = better_balance.index(min(better_balance)) best_merging_position = better_merging_index[best_balance_index] bins_list = all_possible_merging[best_merging_position][‘bins_list‘] bad_by_bin = all_possible_merging[best_merging_position][‘bad_by_bin‘] not_monotone_count = all_possible_merging[best_merging_position][‘not_monotone_count‘] not_monotone_position = FeatureMonotone(bad_by_bin[:, 3])[‘index_of_nonmonotone‘] return bins_list
for i in col: print (i, "\t",Monotone_Merge(df,"bad_ind",i) )

for i in col: print (i, "\t",Monotone_Merge(df2,"bad_ind",i) )

 另一种分箱方法
另一种分箱方法
#该包中对变量进行分箱的原理类似于二叉决策树,只是决定如何划分的目标函数是iv值 import woe.feature_process as fp import woe.eval as eva continuous=[] for i in col: con=fp.proc_woe_continuous(df=df3, var=i,#变量名 global_bt=df3.target.sum(),#正样本总量 global_gt=df3.shape[0]-df3.target.sum(),#负样本总量 min_sample=0.05*df3.shape[0],#单个区间最小样本量阈值 alpha=0.05) continuous.append(con) #该分箱方法缺点分箱太多,不利于业务开展,且手动调整过于繁琐,且容易照成失误

df_continuous=eva.eval_feature_detail(Info_Value_list=continuous) df_continuous.to_csv(‘fx2.csv‘,index=False)
#用热力图看看相关性 colormap = plt.cm.viridis plt.figure(figsize=(12,12)) plt.title(‘Pearson Correlation of Features‘, y=1.05, size=15) sns.heatmap(df.corr(),linewidths=0.1,vmax=1.0, square=True, cmap=colormap, linecolor=‘white‘, annot=True)
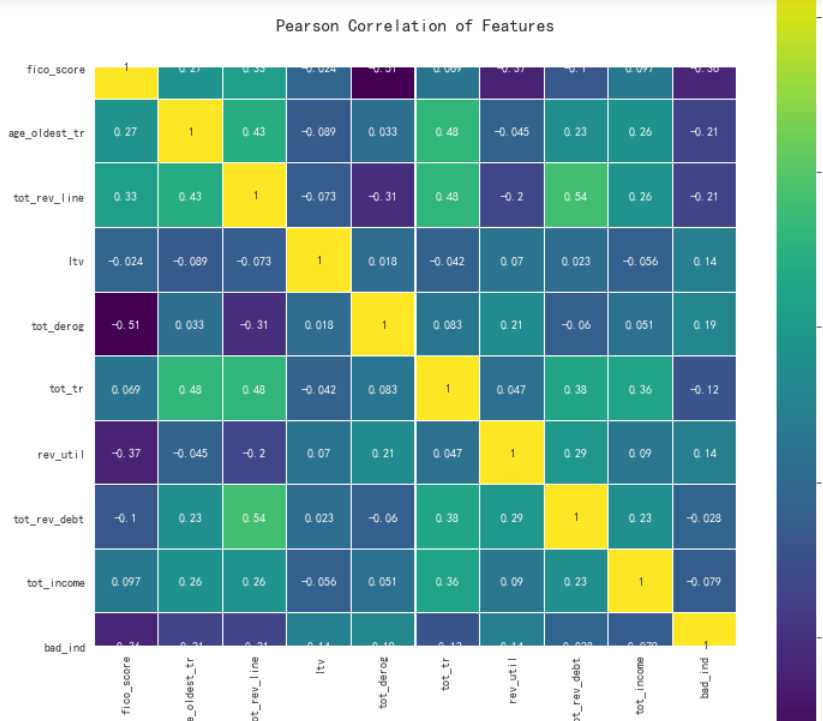
#利用VIF(方差膨胀系数)检验多重共线性 from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF VIF_ls=[] n=df.columns for i in range(len(n)): VIF_ls.append([n[i],int(VIF(df.values,i))]) df_vif=pd.DataFrame(VIF_ls,columns=["name","vif"]) print(df_vif)

#利用协方差计算线性相关性 cor=df[col].corr() cor.iloc[:,:]=np.tril(cor.values,k=-1) cor=cor.stack() cor[np.abs(cor)>0.7]
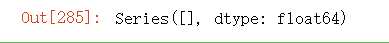
目前为止剩余变量不用处理,开始建模
# 用woe编码替换原属性值,这样可以让系数正则化 for i in range(len(x.columns)): x[x.columns[i]].replace(WOE[x.columns[i]],inplace=True)
x_list=list(df.columns) x_list.remove("bad_ind") x=df[x_list] y=df["bad_ind"]
处理样本不平衡问题
n_sample=y.shape[0] n_pos_sample=y[y==0].shape[0] n_neg_sample=y[y==1].shape[0] print("样本个数:{},正样本占比:{:.2%},负样本占比:{:.2%}".format(n_sample, n_pos_sample/n_sample, n_neg_sample/n_sample))

from imblearn.over_sampling import SMOTE # 导入SMOTE算法模块 #from imblearn.over_sampling import BorderlineSMOTE # 处理不平衡数据 sm = SMOTE(random_state=42) # 处理过采样的方法 x_1, y_1 = sm.fit_sample(x, y) print(‘通过SMOTE方法平衡正负样本后‘) n_sample = y_1.shape[0] n_pos_sample = y_1[y_1 == 0].shape[0] n_neg_sample = y_1[y_1 == 1].shape[0] print(‘样本个数:{}; 正样本占{:.2%}; 负样本占{:.2%}‘.format(n_sample, n_pos_sample / n_sample, n_neg_sample / n_sample))

#切分数据集与训练集 from sklearn.model_selection import train_test_split X_train_1, X_test_1, y_train_1, y_test_1 = train_test_split(x_1,y_1,test_size = 0.3, random_state = 0) X_train, X_test, y_train, y_test = train_test_split(x,y,test_size = 0.3, random_state = 0)
这里切分数据集一眼留作两份,实验在做样本均衡处理与不处理之间的差异
#逻辑回归训练并预测 import itertools from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix,recall_score,classification_report lr = LogisticRegression(C = 1, penalty = ‘l2‘) lr.fit(X_train_1,y_train_1.values.ravel()) y_pred = lr.predict(X_test_1.values)
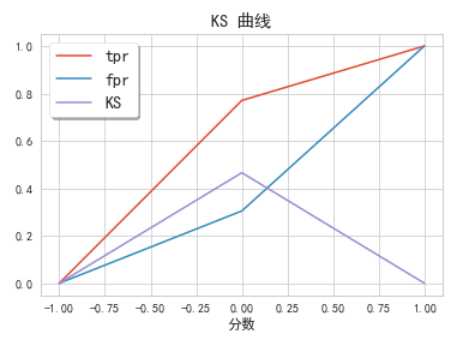
#计算混淆矩阵 from sklearn.metrics import confusion_matrix cnf_matrix = confusion_matrix(y_test_1,y_pred) np.set_printoptions(precision=2) print("模型精确度: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
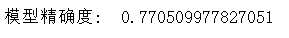
#绘制混淆矩阵 plt.figure(figsize=(5,3)) sns.heatmap(cnf_matrix)
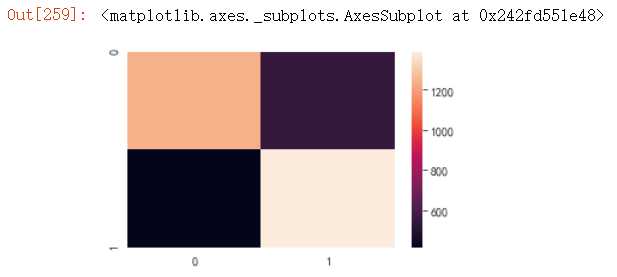
#绘制ROC曲线 from sklearn.metrics import roc_curve, auc fpr,tpr,threshold = roc_curve(y_test_1,y_pred, drop_intermediate=False) ###计算真正率和假正率 roc_auc = auc(fpr,tpr) ###计算auc的值 ks=max(tpr-fpr) plt.figure() lw = 2 plt.figure(figsize=(10,10)) plt.plot(fpr, tpr, color=‘darkorange‘, lw=lw, label=‘ROC curve (area = %0.2f)‘ % roc_auc) ###假正率为横坐标,真正率为纵坐标做曲线 plt.plot([0, 1], [0, 1], color=‘navy‘, lw=lw, linestyle=‘--‘) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel(‘False Positive Rate‘) plt.ylabel(‘True Positive Rate‘) plt.title("ROC 曲线") plt.legend(loc="lower right") plt.show() print("auc:{} ks:{}".format(roc_auc,ks))
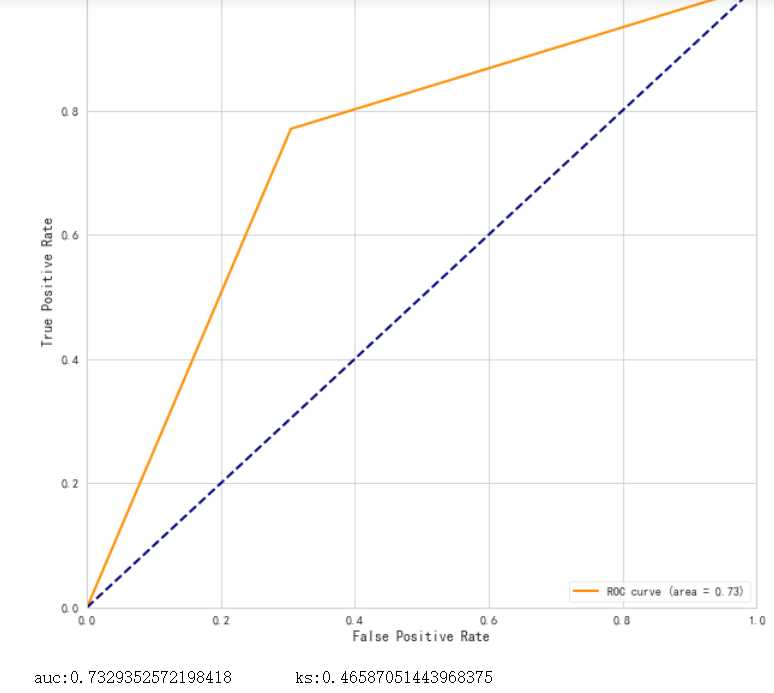
# 利用sklearn.metrics中的roc_curve算出tpr,fpr作图 fig, ax = plt.subplots() ax.plot(1 - threshold, tpr, label=‘tpr‘) # ks曲线要按照预测概率降序排列,所以需要1-threshold镜像 ax.plot(1 - threshold, fpr, label=‘fpr‘) ax.plot(1 - threshold, tpr-fpr,label=‘KS‘) plt.xlabel(‘分数‘) plt.title(‘KS 曲线‘) #plt.xticks(np.arange(0,1,0.2), np.arange(1,0,-0.2)) #plt.xticks(np.arange(0,1,0.2), np.arange(score.max(),score.min(),-0.2*(data[‘反欺诈评分卡总分‘].max() - data[‘反欺诈评分卡总分‘].min()))) plt.figure(figsize=(20,20)) legend = ax.legend(loc=‘upper left‘, shadow=True, fontsize=‘x-large‘) plt.show()
coef=lr.coef_#模型输出系数 intercept=lr.intercept_#模型输出截距 #变量集v与对应系数coef组合:v_coef df_v=pd.DataFrame(col) df_coef=pd.DataFrame(coef.T,index=col) #v_coef=pd.concat([df_v,df_coef],axis=1) #v_coef.columns=[‘var_name‘,‘coef‘] #v_coef df_coef.T

intercept

#输出评分卡 #假设比率为1/20 时 分值是500,比率每翻倍一次的20分 B=20/np.log(2) A=500+B*np.log(1/20) basescore=round(A-B*1.63,0) #基准分四舍五入取 scores=woe0*B for i in col: scores[i]=scores[i].apply(lambda x:-round(x*df_coef.T[i],0)) print("基准分等于","\t",basescore) print("各项得分等于") scores
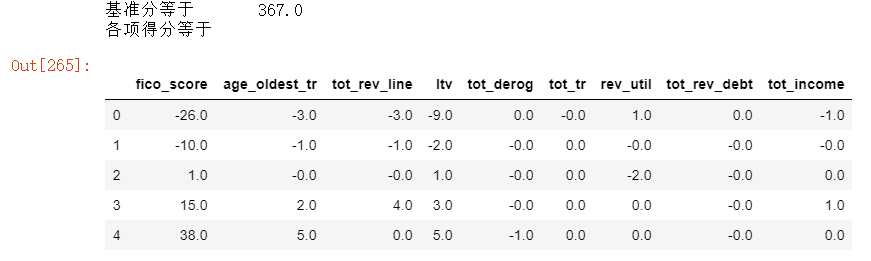
以上为分箱最小箱比列为0 ,且经过样本平衡处理的结果
之后分别计算了不同参数下的结果
1.以上为分箱最小箱比列为0 ,未作样本平衡处理结果
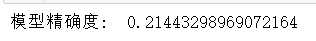
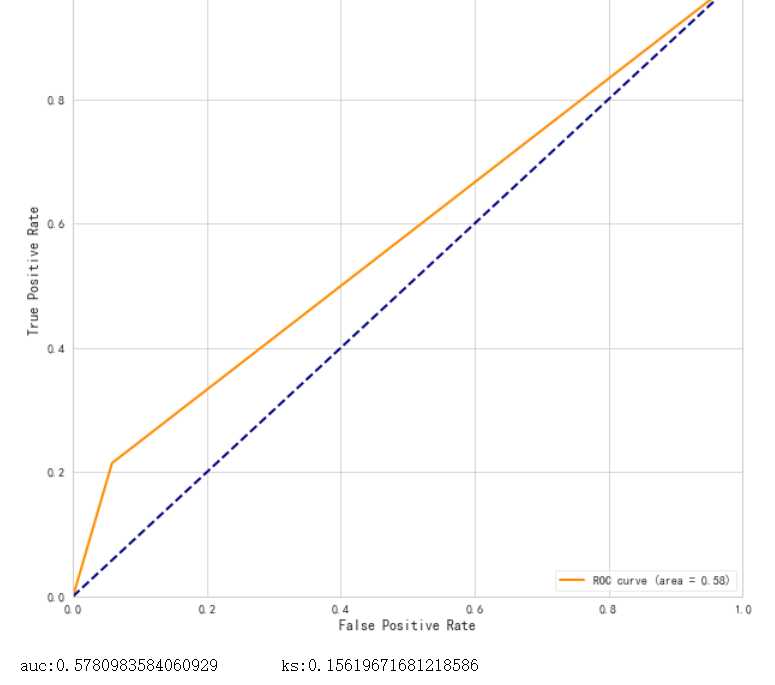
结果很差,可能是因为样本数据较小,所以样本平衡显得尤其重要
2.分箱最小箱比列为0 ,且经过样本平衡处理的结果,经过单调性检验并合并分箱之后的结果
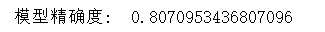
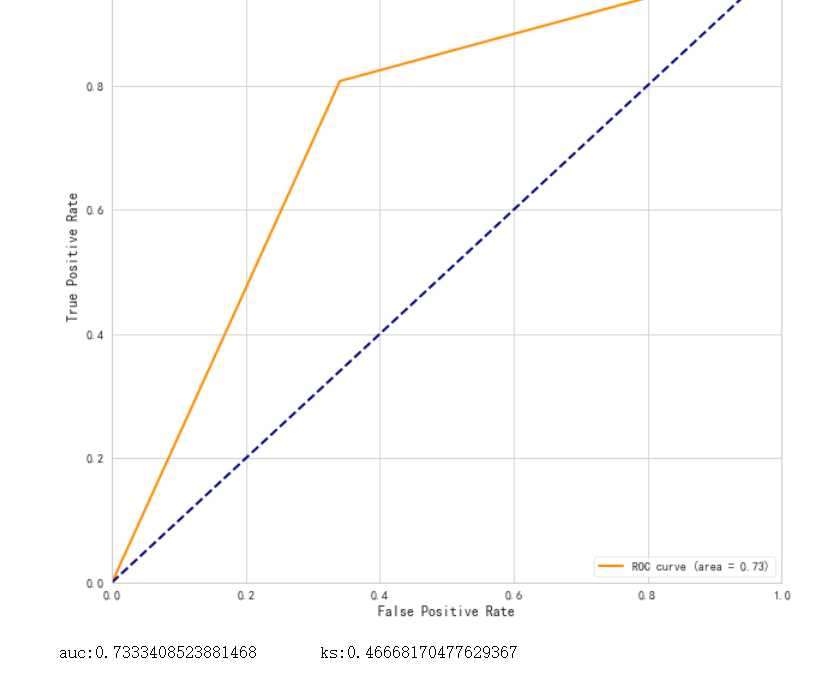
精确度有所提升,但是模型效力提升效果不显著
之后的样本建模任然没有太大变化。
总结:
1.分箱方案的选择,可能直接影响到特征的选择,所以需要多尝试几次,尽量选择最优的方案
2.模型的建立,本身是一个所有步骤不断迭代的过程,从缺失值填充开始,就需要不断的尝试不同方案,用来提升模型效力
还缺少一个完整的评分卡展示。。。。后面再补上
标签:actor fonts 不执行 enumerate point 缺失值 statistic reset 坐标
原文地址:https://www.cnblogs.com/Koi504330/p/12333807.html