标签:理解 mil 场景 记录 应用 ++ 输出 最大 默认
应用场景-背包问题
|
物品 |
重量 |
价格 |
|
吉他(G) |
1 |
1500 |
|
音响(S) |
4 |
3000 |
|
电脑(L) |
3 |
2000 |
背包问题:有一个背包,容量为4磅 , 现有如下物品
动态规划算法介绍
应用场景-背包问题-解决思路
|
物品 |
重量 |
价格 |
|
吉他(G) |
1 |
1500 |
|
音响(S) |
4 |
3000 |
|
电脑(L) |
3 |
2000 |
背包问题:有一个背包,容量为4磅 , 现有如下物品
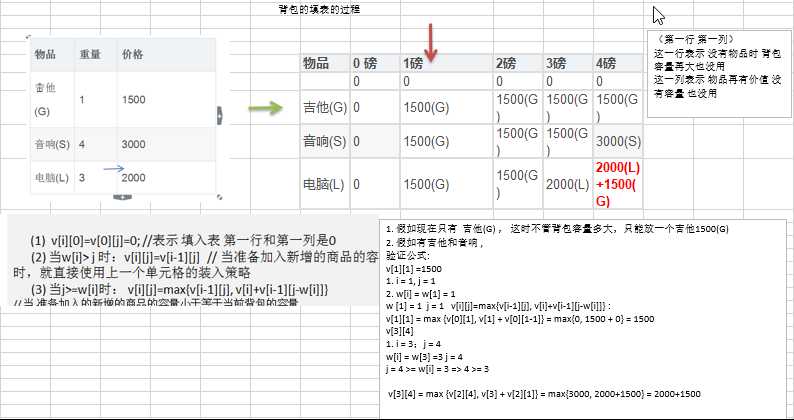
算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是0
(2) 当w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量 时,就直接使用上一个单元格的装入策略
(3) 当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// 当 准备加入的新增的商品的容量小于等于当前背包的容量,
// 装入的方式:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i] : 表示当前商品的价值
v[i-1][j-w[i]] : 装入i-1商品,到剩余空间j-w[i]的最大值
v[i]+v[i-1][j-w[i]] 就是先把当前商品加入背包 再加入当前剩余空间可以放的最大价值的商品 (上面那句不好理解 看这句 直接就解释了后半句是什么意思)
max{v[i-1][j], v[i]+v[i-1][j-w[i]]} 看那个策略可以放入价值更高的商品
当j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
使用填表过程来理解背包问题 先是自己用人的思维
再把公式代入 找一个结果 进行验算 理解这个公式
完整代码
package com.atguigu.dynamic; public class KnapsackProblem { public static void main(String[] args) { // TODO Auto-generated method stub int[] w = {1, 4, 3};//物品的重量 int[] val = {1500, 3000, 2000}; //物品的价值 这里val[i] 就是前面讲的v[i] int m = 4; //背包的容量 int n = val.length; //物品的个数 //创建二维数组, //v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值 可以找一个坐标 去验证是否是最大价值 int[][] v = new int[n+1][m+1]; //为了记录放入商品的情况,我们定一个二维数组 int[][] path = new int[n+1][m+1]; //初始化第一行和第一列, 这里在本程序中,可以不去处理,因为默认就是0 for(int i = 0; i < v.length; i++) { v[i][0] = 0; //将第一列设置为0 } for(int i=0; i < v[0].length; i++) { v[0][i] = 0; //将第一行设置0 } //根据前面得到公式来动态规划处理 for(int i = 1; i < v.length; i++) { //不处理第一行 i是从1开始的 for(int j=1; j < v[0].length; j++) {//不处理第一列, j是从1开始的 //公式 if(w[i-1]> j) { // 因为我们程序i 是从1开始的,因此原来公式中的 w[i] 修改成 w[i-1] v[i][j]=v[i-1][j]; } else { //说明: //因为我们的i 从1开始的, 因此公式需要调整成 //v[i][j]=Math.max(v[i-1][j], val[i-1]+v[i-1][j-w[i-1]]); //v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]); //为了记录商品存放到背包的情况,我们不能直接的使用上面的公式,需要使用if-else来体现公式 //理解过来就是 原策略价值不如 现在加入当前商品和剩余空间加入最大价值商品 的总和 if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) { v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]]; //把当前的情况记录到path 最优的情况(原策略价值不如 现在加入当前商品和剩余空间加入最大价值商品 的总和 ) path[i][j] = 1; } else { v[i][j] = v[i - 1][j]; } } } } //输出一下v 看看目前的情况 就是打印那张表 for(int i =0; i < v.length;i++) { for(int j = 0; j < v[i].length;j++) { System.out.print(v[i][j] + " "); } System.out.println(); } System.out.println("============================"); //输出最后我们是放入的哪些商品 //遍历path, 这样输出会把所有的放入情况都得到, 其实我们只需要最后的放入 // for(int i = 0; i < path.length; i++) { // for(int j=0; j < path[i].length; j++) { // if(path[i][j] == 1) { // System.out.printf("第%d个商品放入到背包\n", i); // } // } // } //动脑筋 将最优的解中的商品输出 是通过计算出来的 int i = path.length - 1; //行的最大下标 int j = path[0].length - 1; //列的最大下标 while(i > 0 && j > 0 ) { //从path的最后开始找 if(path[i][j] == 1) { System.out.printf("第%d个商品放入到背包\n", i); j -= w[i-1]; //w[i-1] //将容量-放入的这个商品的容量 所以再只能在剩余容量范围内的商品中找 相当于去除了一些不符合的数据 //自己回溯 找path[i][j] == 1 //第一次循环完了 i= 2 j = 1 //发现path[2][1] 当时不是最优 所以是选取的上一个表格的值 也就是path[1][1] 的值 } i--; } } }
标签:理解 mil 场景 记录 应用 ++ 输出 最大 默认
原文地址:https://www.cnblogs.com/cnng/p/12334032.html