标签：点子   经典   等级   比较   区间   ref   关联   max   hub   

物元分析方法是中国学者蔡文于20世纪80年代提出的用于解决矛盾问题的技术方法,是研究物元及其变化规律,解决现实世界中不相容问题的有效方法,可应用于生态环境,水资源承载力,农用地分级和土地生态水平等综合评价研究中.

本文主要介绍了熵权可拓物元模型的相关概念与该模型的建立过程.

2 概念

2.1 物元

物元分析法的主要思想是把事物用"事物,特征,量值"(分别用N,C,V表示)3个要素以有序三元组的形式来描述,这个三元组就叫物元.

2.2 可拓

可拓学是以蔡文,杨春燕研究员等为首的中国学者创立的新学科.

可拓学是研究事物拓展的可能性和开拓创新的规律与方法,并用以解决矛盾问题,是一门交叉学科,基本理论是可拓论,特有的方法是可拓方法,逻辑基础是可拓逻辑,与各领域的交叉融合形成可拓工程.可拓论,可拓方法(也叫可拓创新方法),可拓工程构成了可拓学.

(图源)

可拓评价法是综合评价法的重要分支,通过借助可拓学的基本理论,从定性和定量两个角度将矛盾问题转化为多个特性的择近原则问题,从而得出事物之间的内部规律.

2.3 相容与不相容问题

当所给的条件能达到要实现的目标时,称为相容问题,当所给的条件不能达到要实现的目标时,则为不相容问题.不相容问题在一定条件下不能用常规办法解决,用数学公式表示,就是:

W = R × r

其中W表示问题,R表示目标,r表示条件,在条件处于r的情况下,通过一般常规方法,不能实现目标R,这时问题W就是不相容问题.不相容问题具有时效性,因为一些不相容问题,虽然只能用非常规办法解决,但随着时代发展,又可以用常规方法加以解决.

2.4 物元分析

物元分析是研究物元,探讨如何求解不相容问题的一种方法,以研究促进事物转化,解决不相容问题为核心内容,是研究求解不相容问题时出点子,想办法的规律与方法的理论.物元分析的突出特点是创立了物元这一新概念,并建立了物元变换理论.求解不相容问题,必须同时考虑质和量,才可以使问题得到解决.

2.5 物元可拓分析

物元可拓分析是利用物元模型与可拓集合把系统研究中的实际问题转化为形式化的问题模型以及描述问题解决过程的模型,从而有效地解决矛盾,为决策提供数据,将不相容问题转化为相容问题,使问题得到合理解决.

2.6 熵权法

传统的AHP法等确定评价指标权重的方法往往比较主观,容易造成评价结果由于人的主观因素而形成偏差.熵权法根据评价指标变异程度的大小来确定指标权重,指标变异程度越大,信息熵越小,该指标权重值越大,反之则越少.熵权法的主要目的是减少主观性,使对评价对象进行的评价更加客观化.

3 步骤

3.1 确定物元

将要评价的事物记作N,其特征记为c,特征量值记为v,假设N有多个特征:

这n个特征对应的量值为:

则可表示为:

R为n维物元,简记为:

c表示要评价的物元的n个特征:

v表示n个特征的量值:

3.2 确定经典域

经典域是根据将要评价的物元的特征及其量值所在的区间确定的,假设将评价等级分为m级,用

表示第j个等级,用

表示第i个评价指标,用

表示在等级j下第i个评价指标的取值范围,这个取值范围用区间

表示,则N,c,v以有序三元组的形式结合起来即为经典域物元Rj:

3.3 确定节域

节域用Rp表示,vpi为节域物元关于特征ci的量值范围:

其中

就是

第i个指标的所有范围的并集.

节域物元Rp可表示为:

3.4 确定待评物元

设有y个待评事物,把待评对象Nx的物元表示为Rx:

3.5 确定关联函数

令有界区间X

的模定义为:

某一点x到区间X的距离为:

则关联函数的k定义为:

3.6 确定关联度

关联函数表达式为:

其中kxj(vi)表示第x个待评物元,第j个等级,第i个指标的关联度,vxi为第x个待评价物元的第i个量值,vji为第j个经典域物元第i个指标的量值范围,|vji|为3.5中定义的区间的模,vpi为节域物元第i个指标的量值范围.

为3.5中的公式,表示第x个待评物元第i个量值vi与对应经典域量值范围vji的有限区间的距离.

通过该式子会计算出y × n × m个关联度(y为待评物元个数,n为指标的个数,m为划分的等级的个数):

3.7 确定权重

需要计算n个指标对应的n个权重:

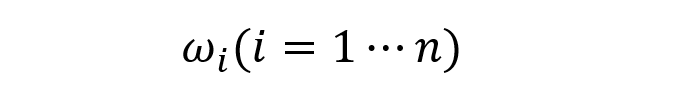
四个步骤:确定初始矩阵,归一处理,计算熵值,计算熵权.

3.7.1 确定初始矩阵

初始矩阵即为要评价的y个物元中的n个指标的量值构成的矩阵,用X表示:

3.7.2 指标归一

将初始矩阵归一化处理,得到归一化矩阵B:

其中:

min(xi)/max(xi)为矩阵X第i行的最小/最大值.

另一种计算方式为:

3.7.3 计算熵值

需要计算n个熵值:

m为划分的等级的个数. fij为:

分子为bij,分母为矩阵B第i行之和.

一般为了使对数有意义,需要对上式进行修正,分子分母都"加1":

因此修正后的熵值Hi为:

3.7.4 计算熵权

计算n个指标对应的n个熵权:

n个熵权,满足和等于1:

3.8 确定综合关联度

需要计算y*m个综合关联度,用K表示:

其中

Nx表示第x个评价事物,wi为第i个指标的熵权,kj(vi)为第j个等级第i个指标的关联度.

(注:x其实不一定从1开始,如评价的事物与年份有关,则x从年份开始,如x=2000,y=2010).

4 参考

github

熵权可拓物元模型

标签：点子   经典   等级   比较   区间   ref   关联   max   hub   

原文地址：https://blog.51cto.com/13996197/2472357