标签:进化 原函数 功能 实验 深度 适应 穷举 理论 突变
定义了基于树的候选激活函数搜索空间,并通过变异搜索、交叉搜索和穷举搜索进行了研究。
优化的激活函数
介绍了搜索空间、突变和交叉实现以及整个演化算法。
每个激活函数被定义为一个由一元函数和二元函数组成的树结构。函数按层分组,这样两个一元函数就会被转换成二元函数。
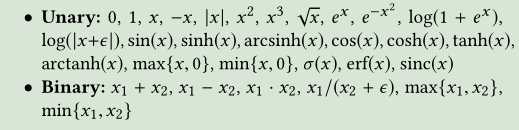
变异
在突变中,激活函数树中的一个节点是随机均匀选择的。该节点处的函数被搜索空间中的另一个随机函数替换。一元函数总是被一元函数代替,二元函数总是被二元函数代替。突变如图1所示。从理论上讲,突变本身就足以构成任何激活功能。实验表明,交叉可以提高发现良好激活函数的速度。
突变的形式:
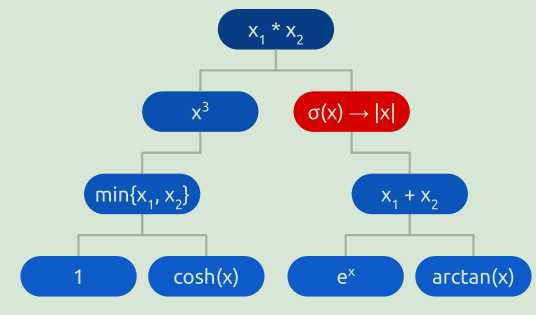
例如:原函数为:(min{ 1 ,cosh(x)}) 3 ∗σ(e x + arctan(x)).突变后将变成 (min{ 1 ,cosh(x)}) 3 ∗|e x +arctan(x)|.
交叉
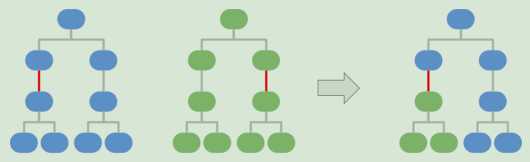
交叉的形式:需要注意的是:子树必须具有相同的深度,以确保得到的子树激活函数与其父树属于相同的搜索空间。
进化
N个激活函数,在给定的训练数据集上用每个函数训练神经网络。每个函数都被赋予一个适应度pi。
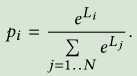
标签:进化 原函数 功能 实验 深度 适应 穷举 理论 突变
原文地址:https://www.cnblogs.com/student-xin/p/12335158.html