标签:指定 高斯 href img 获得 math 高斯分布 不能 无监督学习
本博客根据 百面机器学习,算法工程师带你去面试 一书总结归纳,公式图片均出自该书.
本博客仅为个人总结学习,非商业用途,侵删.
网址 http://www.ptpress.com.cn
高斯混合模型(Gaussian Mixed Model, GMM) 是一种常见的聚类算法,与K均值算法类似,同样使用了EM算法进行迭代计算。 高斯混合模型假设每个簇的数据都是符合高斯分布(又叫正态分布) 的, 当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。
下面是一个高斯混合分布得例子,如果只用一个高斯分布来拟合图中的数据,则如下图:
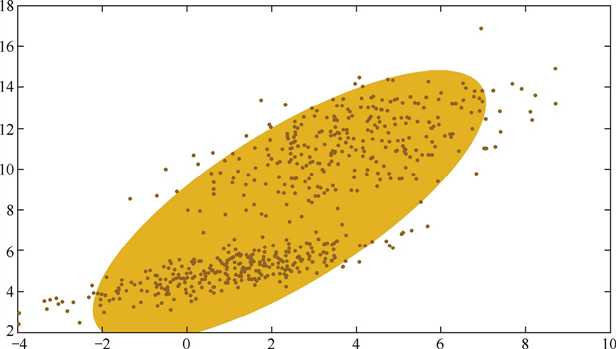
由于图中的数据明显分为两簇,因此只用一个高斯分布来拟合是不合理的,需要推广到多个,如下图就是用两个高斯分布来拟合:
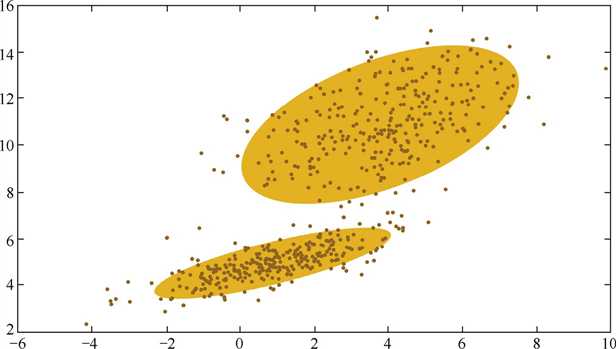
这就引出了高斯混合模型, 即用多个高斯分布函数的线形组合来对数据分布进行拟合。 理论上, 高斯混合模型可以拟合出任意类型的分布。
高斯混合模型的核心思想是, 假设数据事实上有多个类,可以看作其是从多个高斯分布中生成出来的。 在该假设下,每个单独的分模型都是标准高斯模型,其均值\(μ_i\)和方差\(Σ_i\)是待估计的参数。 此外,每个分模型都还有一个参数\(π_i\),可以理解为权重或生成数据的概率。
所以高斯混合模型的公式是:
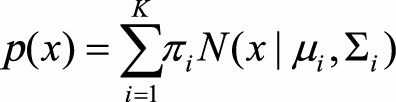
其中,K是分布的个数。即表示为K个分布得加权和。
通常我们并不能直接得到高斯混合模型的参数, 而是观察到了一系列数据点, 给出一个类别的数量K后, 希望求得最佳的K个高斯分模型。 因此,高斯混合模型的计算,便成了最佳的均值μ,方差Σ、权重π的寻找。
此时可以使用EM算法框架来求解该最优化的问题。EM算法在最大化目标函数时, 先固定一个变量使整体函数变为凸优化函数, 求导得到最值, 然后利用最优参数更新被固定的变量, 进入下一个循环。
在高斯混合模型中,EM算法的迭代过程如下:
1) E步骤。 根据当前的参数, 计算每个点由某个分模型生成的概率
2) M步骤。 使用E步骤估计出的概率, 来改进每个分模型的均值, 方差和权重。
我们并不知道最佳的K个高斯分布的各自3个参数,也不知道每个数据点究竟是哪个高斯分布生成的。 所以每次循环时,先固定当前的高斯分布不变,获得每个数据点由各个高斯分布生成的概率。然后固定该生成概率不变,根据数据点和生成概率,获得一个组更佳的高斯分布。循环往复,直到参数的不再变化,或者变化非常小时,便得到了比较合理的一组高斯分布。
高斯混合模型与K均值算法相似,高斯混合模型也可以用于聚类算法,也需要指定K值;要使用EM算法来求解,并且往往都只能收敛到局部最优。
它的优点是,可以给出一个样本属于某个类的概率是多少;不仅可以用于聚类,还可以用于概率密度估计,并且可以用于生产新的样本。
标签:指定 高斯 href img 获得 math 高斯分布 不能 无监督学习
原文地址:https://www.cnblogs.com/hhhuang/p/12336841.html